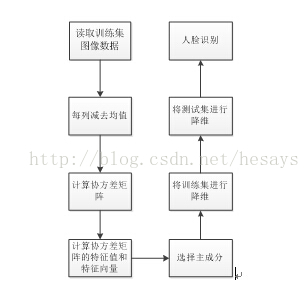
本文主要是介绍PCA与LDA,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
共同点
-
降维方法:
- PCA和LDA都是数据降维的方式,它们都能通过某种变换将原始高维数据投影到低维空间。
-
数学原理:
- 两者在降维过程中都使用了矩阵特征分解的思想,通过对数据的协方差矩阵或类间、类内散度矩阵进行特征分解,找到数据中的主要变化方向或分类方向。
-
高斯分布假设:
- PCA和LDA在应用中通常都假设数据符合高斯分布,这一假设是最优的。
不同点
-
监督与非监督:
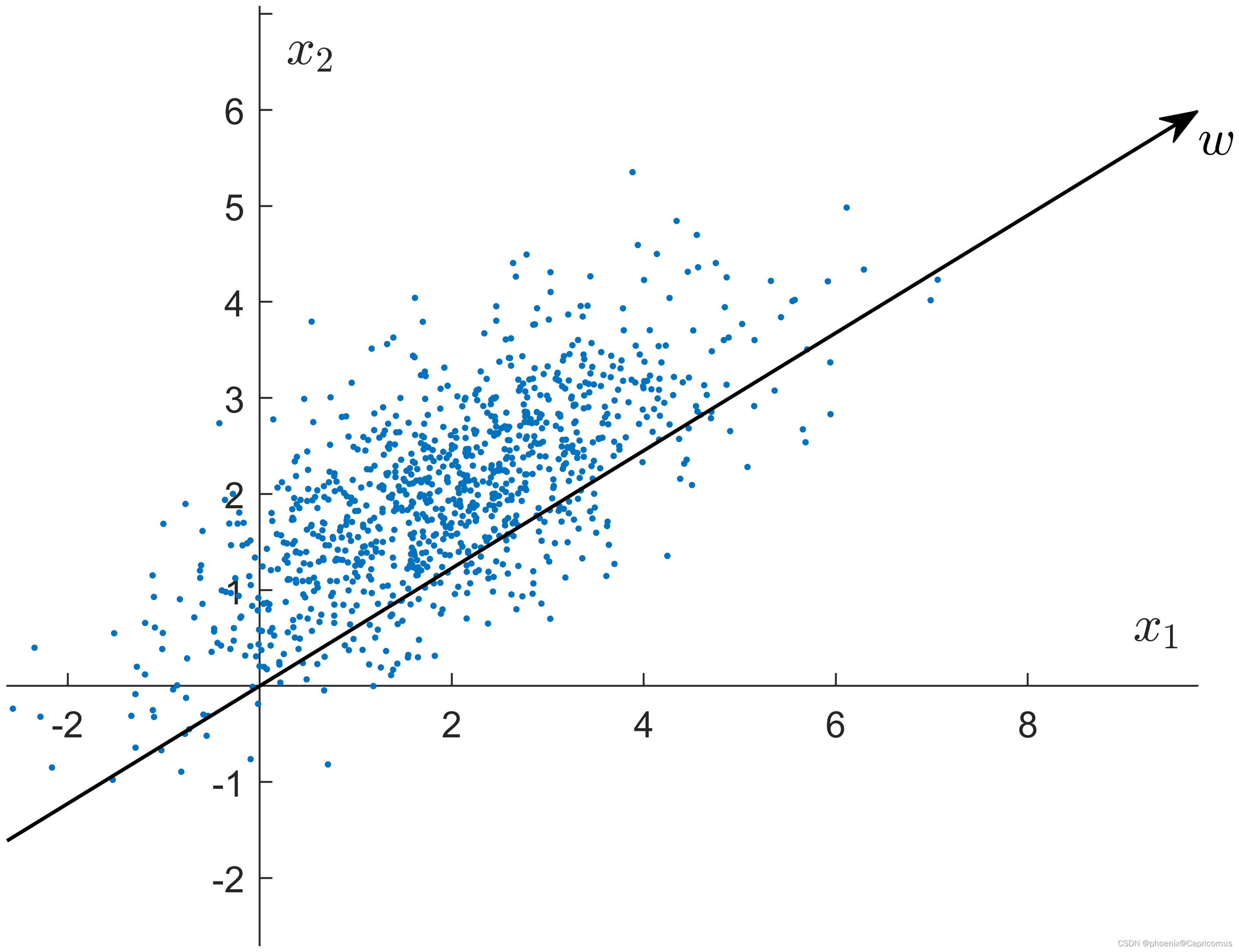
- PCA是一种无监督的降维方法,它不需要知道样本的类别标签。PCA的目标是通过寻找数据中的主成分(即方差最大的方向)来降低数据的维度。
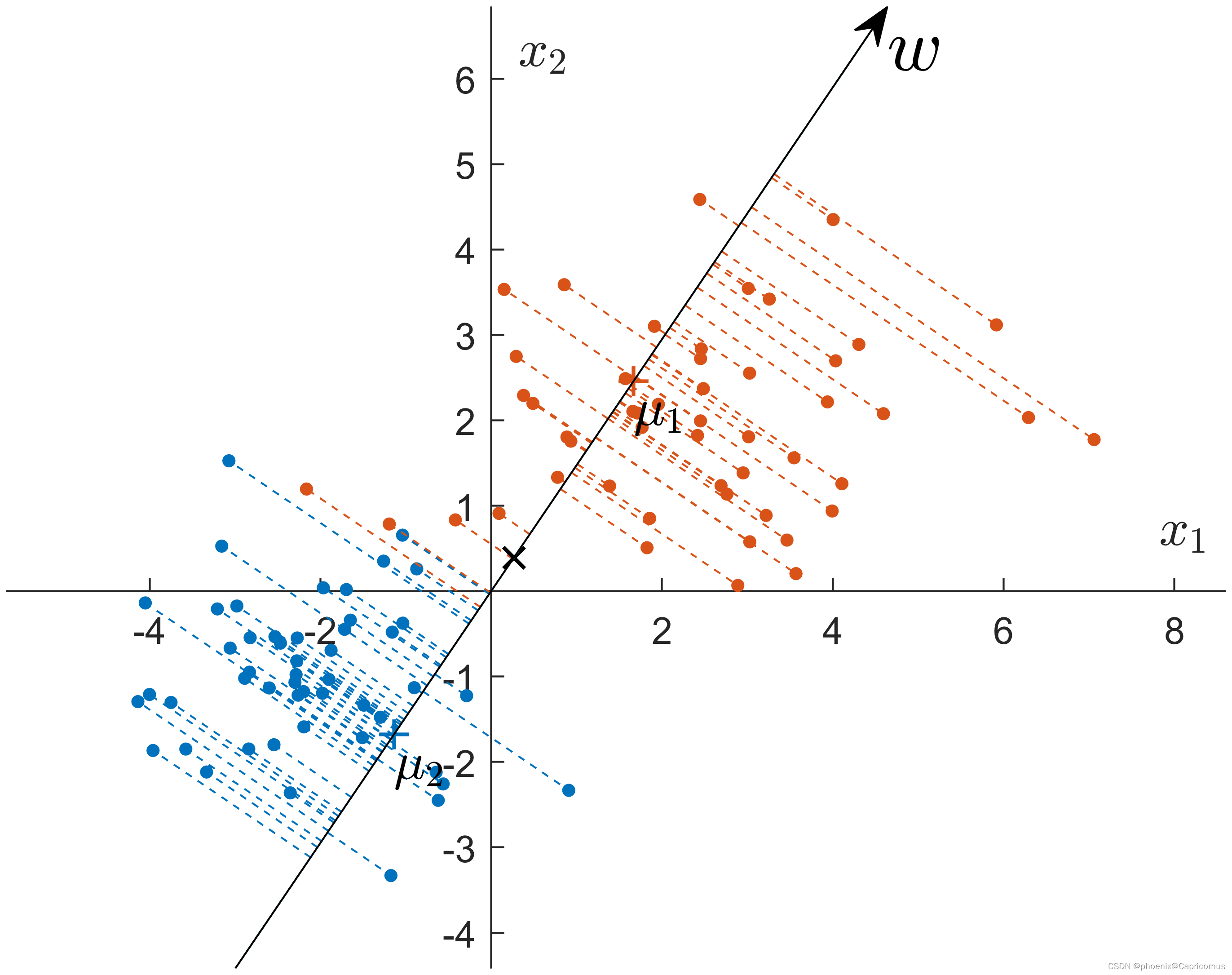
- LDA则是一种有监督的降维方法,它需要知道每个数据点对应的类别标签。LDA的目标是找到一种投影方式,使得投影后不同类别之间的数据均值距离最大,同时相同类别之内的数据方差最小。
-
降维的目标:
- PCA主要关注于找到数据中方差最大的方向,以最大化保留原始数据的信息量。
- LDA则侧重于找到类间差异最大、类内差异最小的方向,以实现更好的分类效果。
-
降维的维度限制:
- PCA在降维时没有明确的维度限制,可以根据需要选择降维后的维度数。
- LDA在降维时最多只能降到类别数k-1的维数,因为LDA需要至少保留一个维度来区分不同的类别。
这篇关于PCA与LDA的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!