Personalized Subgraph Federated Learning，FED-PUB,2023,ICML 2023

本文主要是介绍Personalized Subgraph Federated Learning，FED-PUB,2023,ICML 2023，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

个性化子图联邦学习
paper:Personalized Subgraph Federated Learning
code

Abstract

更大的全局图的子图可能分布在多个设备上，并且由于隐私限制只能在本地访问，尽管子图之间可能存在链接。最近提出的子图联邦学习(FL)方法通过在局部子图上分布式训练图神经网络(gnn)来处理局部子图之间的缺失链接。然而，他们忽略了由全局图的不同社区组成的子图之间不可避免的异质性，从而使局部GNN模型的不相容知识崩溃。为此，我们引入了一种新的子图学习问题——个性化子图学习，该问题侧重于相互关联的局部gnn的联合改进，而不是学习单一的全局模型，并提出了一种新的框架——联邦个性化子图学习(federalpersonalsubgraph learning, FEDPUB)来解决它。由于服务器无法访问每个客户端的子图，因此，federal - pub利用本地gnn的功能嵌入，使用随机图作为输入来计算它们之间的相似度，并使用相似度对服务器端聚合执行加权平均。此外，它在每个客户端学习个性化的稀疏掩码，以选择和更新聚合参数的子图相关子集。我们在六个数据集上验证了我们的FED-PUB的子图FL性能，同时考虑了非重叠和重叠子图，在这些数据集上，它的性能明显优于相关基线。

1.Introduction

现有方法就是一整个图在一个服务器上。例如，在一个社交网络平台上，每一个用户和他/她的社交网络共同构成了一个由所有用户和他们之间的联系组成的巨大网络。然而，在一些实际场景中，每个用户/机构收集自己的私有图，由于隐私限制，这些图只能在本地访问。例如，正如Zhang等人(2021)所描述的那样，每家医院可能都有自己的患者互动网络，以跟踪他们的身体接触或共同诊断疾病;然而，这个图可能不会与他人分享。当子图分布在多个参与者(即客户端)之间时，我们如何在不共享实际数据的情况下协同训练gnn ?最直接的方法是使用GNN执行联邦学习(FL)，其中每个客户端在本地数据上单独训练本地GNN，而中央服务器将来自多个客户端的本地更新的GNN权重聚合为一个。

然而，它面临的一个重要挑战是如何处理子图之间可能缺失的边，这些边没有被单个数据所有者捕获，但可能携带重要信息(参见图1 (A))。最近的子图FL方法(Wu et al.， 2021a;Zhang等人，2021)通过从其他子图扩展局部子图来解决这个问题，如图1 (B)所示。具体来说，它们通过精确地增加其他客户端的其他子图中的相关节点来扩展局部子图(Wu等人，2021a)，或者通过使用其他子图中的节点信息来估计节点(Zhang等人，2021)。然而，这种节点信息的共享可能会损害数据隐私，并可能产生高昂的通信成本。

图1（A）如下图描述的，子图之间存在缺失的信息，有的解决办法是扩张子图，如图（B）

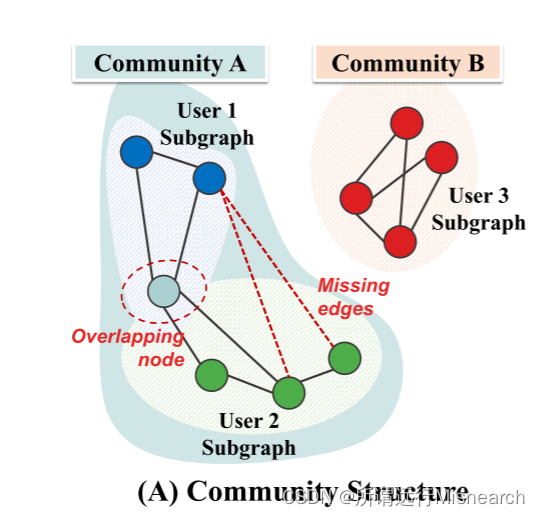
此外，存在一个更重要的挑战，被现有的子图FL方法所忽视。我们观察到，由于子图之间的异质性，它们遭受了很大的性能下降(见图1右)，这是很自然的，因为子图包含全局图的不同部分。具体来说，两个单独的子图——例如，图1 (A)中社区A和社区B中的用户1和用户3子图——有时是完全不相交的，具有相反的属性。同时，两个紧密相连的子图组成了一个社区(如图1 (a)中的社区a中的User 1和2子图)，它们具有相似的特征。然而，在子图FL中考虑图的群落结构引起的这种异质性是具有挑战性的。

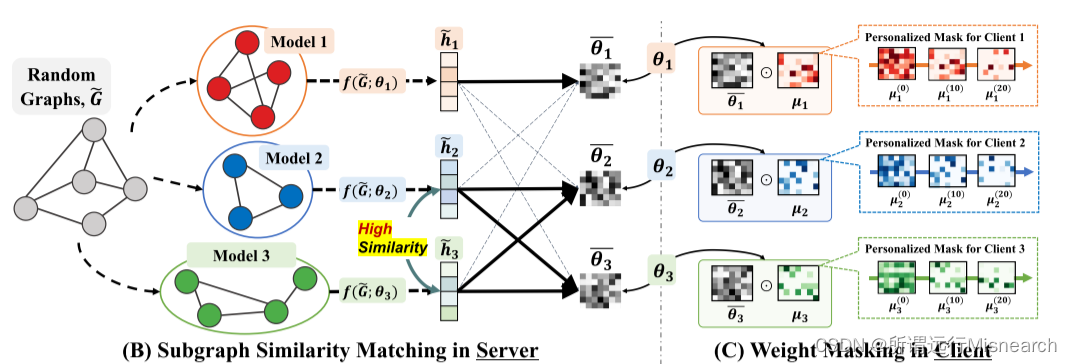
在这一挑战的激励下，我们引入了个性化子图FL的新问题，其目标是通过共享它们之间的权重，共同改进在相互连接的局部子图(例如，属于同一社区的子图)上训练的相互关联的局部模型(参见图1 ©)。然而，实现这种选择性权重共享是具有挑战性的，因为我们不知道每个客户端具有哪个子图，这是由于其本地可访问性。为了解决这个问题，我们在随机图上使用gnn的函数嵌入来获得两个局部gnn之间的相似度得分，然后使用它们在服务器上对模型参数进行加权平均。（搞清楚？）。然而，相似性分数只能告诉每个本地模型与其他客户端的相关性如何，而不能告诉哪个参数是相关的。因此，我们进一步学习并在每个客户端的本地GNN上应用个性化的稀疏掩码，以获得与本地子图相关的子网。我们把这个框架称为联邦个性化子图学习(FEDerated Personalized sUBgraph learning, FED-PUB)。

我们在六个数据集上广泛地验证了我们的federal - pub，这些数据集在重叠和不相交的子图FL场景下具有不同数量的客户端。实验结果表明，我们的算法明显优于相关基线。进一步的分析表明，我们的功能嵌入可以发现子图之间的社区结构，并且掩蔽策略可以根据每个客户端的子图定位GNN参数。我们的贡献如下:

• 本文提出了一种新的个性化子图FL问题，该问题旨在对属于同一社区的子图的相关局部模型进行协同改进，这是一个相对被忽视的问题。

• 我们提出了一种新的个性化子图FL框架，该框架在不访问数据的情况下，根据局部模型参数的功能相似度进行加权平均，并学习稀疏掩码，为给定的子图选择相关的子网。

• 我们在重叠和非重叠节点场景的六个真实数据集上验证了我们的FED-PUB，证明了它在相关基线上的有效性。

2.Related Work

Graph Neural Networks (GNNs)：旨在学习节点、边和整个图的表示，是一个被广泛研究的主题(Hamilton, 2020;Zhou et al.， 2020;吴等，2021b;Jo et al.， 2021;Baek et al.， 2021)。在消息传递方案下(Gilmer et al.， 2017)，大多数现有gnn通过聚合其相邻节点和自身的特征来迭代地表示节点。例如，图卷积网络(GCN) (Kipf & Welling, 2017)近似谱图卷积(Hammond等人，2011)，产生相邻节点的平均聚合。类似地，对于每个节点，GraphSAGE (Hamilton et al.， 2017)会聚合其邻居的特征以更新节点表示。虽然它们在单个图的节点分类和链接预测任务上取得了成功，但它们并不能直接适用于具有局部分布图的现实世界系统，在这些系统中，来自不同来源的图不会在参与者之间共享，这导致了训练gnn的联邦学习。

联邦学习(Li et al.， 2021b)对于我们的分布式子图学习问题至关重要。举几个例子，fedag (McMahan et al.， 2017)为每个客户端本地训练一个模型，然后将训练好的模型传输到服务器，而服务器从本地客户端聚合模型权重，然后将聚合模型发送回给它们。然而，由于本地收集的数据在不同客户端之间可能存在很大差异，因此异质性是一个关键问题。为了解决这个问题，FedProx (Li et al.， 2020)提出了正则化项，使局部模型和全局模型之间的权重差异最小化，从而防止局部模型发散到局部训练数据。然而，当本地数据非常异构时，为每个客户协作训练一个个性化模型比学习一个单一的全局模型更合适。FedPer (Arivazhagan等人，2019)就是这样一种方法，它共享基础层，同时为每个客户端提供本地个性化层，以保留本地知识。此外，最近的研究建议提取来自不同客户的输出(Lin等人，2020;Sattler等，2021;Zhu et al.， 2021)，或者直接最小化其模型输出的差异(Makhija et al.， 2022)。然而，与通常研究的图像和文本数据不同，图结构数据是由实例之间的连接定义的，这带来了额外的挑战:缺少边，以及私有子图之间的社区结构。

Graph Federated Learning：最近的一些研究建议使用FL框架在不共享图数据的情况下协同训练gnn (He et al.， 2021;Wang et al.， 2022)，大致可分为子图级和图级方法。图级FL方法假设不同的客户端具有完全不相交的图(例如分子图)，近期工作(Xie et al.， 2021;He et al.， 2022;Tan等人，2022)关注非iid图之间的异质性(即客户端之间图标签的差异)。与具有与一般FL场景相似的挑战的图级FL不同，我们所针对的子图级FL具有独特的图结构挑战:由于子图是更大的全局图的一部分，因此子图之间存在缺失但可能存在的联系。为了处理这种子图之间的缺失链接问题，现有的方法(Wu et al.， 2021a;Zhang et al.， 2021;Yao & Joe-Wong, 2022)通过请求其他子图中的节点信息来增强节点，然后将现有节点与增强的节点连接起来。然而，（在introduction也介绍过）在节点信息共享过程中，这种方案可能会损害数据隐私约束，并且还会增加客户端之间的通信开销。与他们专注于缺失链接的问题不同，我们的子图FL方法通过探索子图社区，以完全不同的视角解决了新问题(Girvan & Newman, 2002;Radicchi et al.， 2004)，它们是密集连接子图的群。

3.Problem Statement

我们解释了gnn和FL，然后定义了位于它们交叉点的个性化子图FL的新问题。

Graph Neural Networks:公式1，

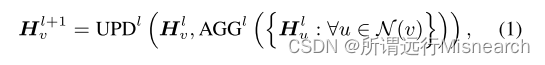
Federated Learning:

• K个client

然后，流行的FL算法FedAvg (McMahan et al.， 2017)的工作原理如下:

它在步骤2和3之间迭代，直到到达最后一轮R，它只共享参数而不共享私有本地数据。

Challenges in Subgraph FL：虽然上述FL在图像和文本数据上工作得很好，但由于图的独特特性，将这种FL方案应用于图结构数据存在不小的挑战。特别是，与每个实例Xi独立于其他图像的图像域不同，图中的每个节点v总是受到其与相邻节点N(v)的关系的影响。并且，一个局部图Gi可以是一个更大的全局图G: Gi G的子图。在这种情况下，两个不同客户端的子图之间可能存在缺失边。为了解决这个问题，现有的方法(Wu et al.， 2021a;Zhang et al.， 2021)根据其他客户Gi上的子图的节点信息估算局部子图Gk的节点，然后用估算的节点扩展现有节点。（第三次提到现有方法如何解决的）

然而，还有一个更具挑战性的问题。假设我们有一个由所有子图组成的全局图。然后，存在这样的子图的群(Girvan & Newman, 2002;Radicchi et al.， 2004;Porter et al.， 2009)，其中同一社区内的子图之间的连接比社区外的子图更密集。形式上，一个全局图G可以分解成T个不同的群落，其中i-群落Ci = (Vi, Ei)由密集连接的节点组成。然后，在子图FL问题中，局部子图Gj至少归属于一个社区，基于网络同质性(McPherson et al.， 2001)，同一社区内紧密连接的子图具有相似的性质，而两个相反社区中的子图则不具有相似的性质。群落的这种分布异质性可能导致朴素的FL算法使来自不同群落的不相容知识崩溃。

Personalized Subgraph FL：为了缓解上述知识崩溃问题，我们的目标是通过对局部模型参数进行个性化加权平均和屏蔽来实现子图FL算法的个性化;从而捕获相互关联的子图之间的社区结构。然而，找到一个适用于所有子图的通用参数集(即¯θ)将导致找到次优参数集，因为两个具有稀疏连接的不同社区中的子图由于网络同质性而非常异构。为了解决这一限制，我们提出了一个新的个性化子图FL问题，形式化如下:

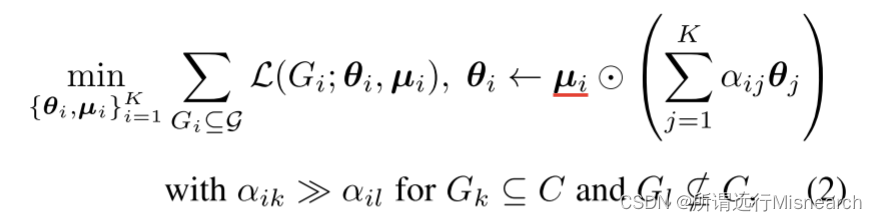
4.Federated Personalized Subgraph Learning

我们提出计算子图的相似度来发现社区，并掩盖不相关社区中的子图的权重。

4.1.Subgraph Similarity Estimation

我们的目标是捕获由一组紧密连接的子图组成的社区。请注意，由于网络同质性，图中的相似实例相互关联更多(McPherson et al.， 2001)，同一社区内的子图应该相似。（第二次提到）。因此，如果我们可以测量子图的相似度，我们就可以将相似的子图分组到社区中。然而，测量子图之间的相似性是具有挑战性的，由于本地可访问性我们不知道每个客户端具有哪个子图。为了在不访问局部数据的情况下仅使用可传递的GNN参数来计算相似度，我们建议使用从子图上工作的GNN获得的辅助信息来近似相似度。

**Model Parameters for Subgraph Similarities：**为了在不访问局部子图的情况下测量它们之间的相似性，我们可以使用模型参数作为代理，这听起来很合理，因为在子图上训练的GNN将把它的知识嵌入到它的参数中。然而，该方案存在明显的缺点，即由于维度的限制，在高维空间中测量的相似度没有意义(Bellman, 1966)，并且随着模型规模的增加，计算参数之间相似度的成本会迅速增加(见图3)。

Functional Embeddings for Subgraph Similarities：为了解决这些限制，我们建议通过向所有GNN模型提供相同的输入，然后使用它们的输出计算相似性来测量GNN的功能相似性，该方法受到Jeong等人(2021)的启发。这里的主要直觉是，我们可以将用神经网络定义的转换视为一个函数，并且我们通过相同输入的输出距离来测量两个网络的功能相似性。然而，与之前使用高斯噪声作为图像分类输入的工作不同，我们在使用gnn时使用随机图作为输入。

Personalized Weight Aggregation：使用相似度度量S(i, j)，我们现在的目标是通过使用不同客户端的模型参数加权和，在处理相似子图的gnn之间共享参数(Chen et al.， 2022;Jeong & Hwang, 2022)。注意，完全忽略来自不同群体的模型参数可能会导致只利用局部目标而忽略全局有用的权重，从而导致次优性能(参见附录C.8)。因此，我们根据功能相似度对所有客户端的局部gnn进行加权平均，如下图(图2 (B)):

5.Experiments

我们在重叠和不相交子图场景下的6个数据集上验证了我们的FED-PUB算法，主要是在节点分类和链路预测任务上。

Datasets:根据Zhang等人(2021)的实验设置，我们通过将数据集划分为一定数量的参与者来构建分布式子图，因为每个FL参与者都有一个子图，该子图是原始图的一部分。然后，我们使用METIS图划分算法(Karypis, 1997)划分他们的图。请注意，与Zhang等人(2021)使用的Louvain算法(Blondel et al.， 2008)不同，该算法需要进一步将划分的子图合并为特定的子图数量，由于无法指定子集的数量(即FL的客户端)，METIS算法可以指定子集的数量，从而做出更合理的实验设置(参见附录C.2)。对于子图之间没有重复节点的非重叠节点场景，我们使用METIS的输出，因为它提供了非重叠分区。对于节点在子图之间重复的重叠场景，我们对分区图的子集(即子图)随机采样多次。详见附录B.1。

Baselines and Our Model：

Implementation Details：

6.Conclusion

在这项工作中，我们引入了一个新的个性化子图FL问题，该问题侧重于通过选择性地利用其他模型的知识来联合改进局部gnn在相互关联的子图(例如属于同一社区的子图)上的工作。所提出的个性化子图FL具有很高的挑战性，因为1)仅在局部可访问的局部子图之间难以计算相似度;2)在权重聚合过程中，在异构子图上工作的局部gnn之间存在知识崩溃问题。为此，我们提出了一种新的个性化子图FL框架，称为联邦个性化子图学习(FEDerated personalized subgraph learning, federal - pub)，它使用随机图上的GNN模型的功能嵌入来估计子图之间的相似性，并使用它们对每个客户端的局部模型进行加权平均。此外，我们掩盖了全局给定的权重，只关注每个社区和客户的相关子网。我们在多个具有重叠和非重叠子图的基准数据集上广泛验证了我们的FED-PUB框架，在这些数据集上，我们的FED-PUB显著优于相关基线。进一步的分析表明，我们的相似度匹配方法在捕获群落结构方面是有效的，我们的权重掩盖策略在处理子图异质性方面也是有效的。

这篇关于Personalized Subgraph Federated Learning，FED-PUB,2023,ICML 2023的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---