本文主要是介绍Python 全栈体系【四阶】(五十八),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第五章 深度学习
十三、自然语言处理(NLP)
3. 文本表示
3.1 One-hot
One-hot(独热)编码是一种最简单的文本表示方式。如果有一个大小为V的词表,对于第i个词 w i w_i wi,可以用一个长度为V的向量来表示,其中第i个元素为1,其它为0.例如:
减肥:[1, 0, 0, 0, 0]
瘦身:[0, 1, 0, 0, 0]
增重:[0, 0, 1, 0, 0]
One-hot词向量构建简单,但也存在明显的弱点:
- 维度过高。如果词数量较多,每个词需要使用更长的向量表示,造成维度灾难;
- 稀疏矩阵。每个词向量,其中只有一位为1,其它位均为零;
- 语义鸿沟。词语之间的相似度、相关程度无法度量。
3.2 词袋模型
词袋模型(Bag-of-words model,BOW),BOW模型假定对于一个文档,忽略它的单词顺序和语法、句法等要素,将其仅仅看作是若干个词汇的集合,文档中每个单词的出现都是独立的,不依赖于其它单词是否出现。例如:
我把他揍了一顿,揍得鼻青眼肿
他把我走了一顿,揍得鼻青眼肿
构建一个词典:
{"我":0, "把":1, "他":2, "揍":3, "了":4 "一顿":5, "鼻青眼肿":6, "得":7}
再将句子向量化,维数和字典大小一致,第i维上的数值代表ID为i的词在句子里出现的频次,两个句子可以表示为:
[1, 1, 1, 2, 1, 1, 1, 1]
[1, 1, 1, 2, 1, 1, 1, 1]
词袋模型表示简单,但也存在较为明显的缺点:
- 丢失了顺序和语义。顺序是极其重要的语义信息,词袋模型只统计词语出现的频率,忽略了词语的顺序。例如上述两个句子意思相反,但词袋模型表示却完全一致;
- 高维度和稀疏性。当语料增加时,词袋模型维度也会增加,需要更长的向量来表示。但大多数词语不会出现在一个文本中,所以导致矩阵稀疏。
3.3 TF-IDF
TF-IDF(Term Frequency-Inverse Document Frequency,词频-逆文档频率)是一种基于传统的统计计算方法,常用于评估一个文档集中一个词对某份文档的重要程度。其基本思想是:一个词语在文档中出现的次数越多、出现的文档越少,语义贡献度越大(对文档区分能力越强)。其表达式为:
T F − I D F = T F i j × I D F i = n j i ∑ k n k j × l o g ( ∣ D ∣ ∣ D i ∣ + 1 ) TF-IDF = TF_{ij} \times IDF_i =\frac{n_{ji}}{\sum_k n_{kj}} \times log(\frac{|D|}{|D_i| + 1}) TF−IDF=TFij×IDFi=∑knkjnji×log(∣Di∣+1∣D∣)
该指标依然无法保留词语在文本中的位置关系。该指标前面有过详细讨论,此处不再赘述。
3.4 共现矩阵
共现(co-occurrence)矩阵指通过统计一个事先指定大小的窗口内的词语共现次数,以词语周边的共现词的次数做为当前词语的向量。具体来说,我们通过从大量的语料文本中构建一个共现矩阵来表示词语。例如,有语料如下:
I like deep learning.
I like NLP.
I enjoy flying.
则共现矩阵表示为:
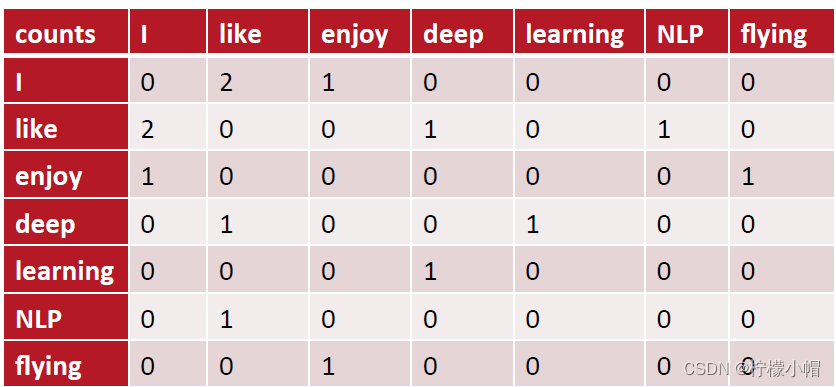
矩阵定义的词向量在一定程度上缓解了one-hot向量相似度为0的问题,但没有解决数据稀疏性和维度灾难的问题。
3.5 N-Gram表示
N-Gram模型是一种基于统计语言模型,语言模型是一个基于概率的判别模型,它的输入是个句子(由词构成的顺序序列),输出是这句话的概率,即这些单词的联合概率。
N-Gram本身也指一个由N个单词组成的集合,各单词具有先后顺序,且不要求单词之间互不相同。常用的有Bi-gram(N=2)和Tri-gram(N=3)。例如:
句子:L love deep learning
Bi-gram: {I, love}, {love, deep}, {deep, learning}
Tri-gram: {I, love, deep}, {love deep learning}
N-Gram基本思想是将文本里面的内容按照字节进行大小为n的滑动窗口操作,形成了长度是n的字节片段序列。每一个字节片段称为一个gram,对所有gram的出现频度进行统计,并按照事先设置好的频度阈值进行过滤,形成关键gram列表,也就是这个文本向量的特征空间,列表中的每一种gram就是一个特征向量维度。
3.6 词嵌入
3.6.1 什么是词嵌入
词嵌入(word embedding)是一种词的向量化表示方式,该方法将词语映射为一个实数向量,同时保留词语之间语义的相似性和相关性。例如:
| Man | Women | King | Queen | Apple | Orange | |
|---|---|---|---|---|---|---|
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royal | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Age | 0.03 | 0.02 | 0.70 | 0.69 | 0.03 | -0.02 |
| Food | 0.09 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
我们用一个四维向量来表示man,Women,King,Queen,Apple,Orange等词语(在实际中使用更高维度的表示,例如100~300维),这些向量能进行语义的表示和计算。例如,用Man的向量减去Woman的向量值:
e m a n − e w o m a n = [ − 1 0.01 0.03 0.09 ] − [ 1 0.02 0.02 0.01 ] = [ − 2 − 0.01 0.01 0.08 ] ≈ [ − 2 0 0 0 ] e_{man} - e_{woman} = \left[ \begin{matrix} -1 \\ 0.01 \\ 0.03 \\ 0.09 \\ \end{matrix} \right] -\left[ \begin{matrix} 1 \\ 0.02 \\ 0.02 \\ 0.01 \\ \end{matrix} \right] = \left[ \begin{matrix} -2 \\ -0.01 \\ 0.01 \\ 0.08 \\ \end{matrix} \right] \approx \left[ \begin{matrix} -2 \\ 0 \\ 0 \\ 0 \\ \end{matrix} \right] eman−ewoman= −10.010.030.09 − 10.020.020.01 = −2−0.010.010.08 ≈ −2000
类似地,如果用King的向量减去Queen的向量,得到相似的结果:
e m a n − e w o m a n = [ − 0.95 0.93 0.70 0.02 ] − [ 0.97 0.85 0.69 0.01 ] = [ − 1.92 − 0.02 0.01 0.01 ] ≈ [ − 2 0 0 0 ] e_{man} - e_{woman} = \left[ \begin{matrix} -0.95 \\ 0.93 \\ 0.70 \\ 0.02 \\ \end{matrix} \right] -\left[ \begin{matrix} 0.97 \\ 0.85 \\ 0.69 \\ 0.01 \\ \end{matrix} \right] = \left[ \begin{matrix} -1.92 \\ -0.02 \\ 0.01 \\ 0.01 \\ \end{matrix} \right] \approx \left[ \begin{matrix} -2 \\ 0 \\ 0 \\ 0 \\ \end{matrix} \right] eman−ewoman= −0.950.930.700.02 − 0.970.850.690.01 = −1.92−0.020.010.01 ≈ −2000
我们可以通过某种降维算法,将向量映射到低纬度空间中,相似的词语位置较近,不相似的词语位置较远,这样能帮助我们更直观理解词嵌入对语义的表示。如下图所示:
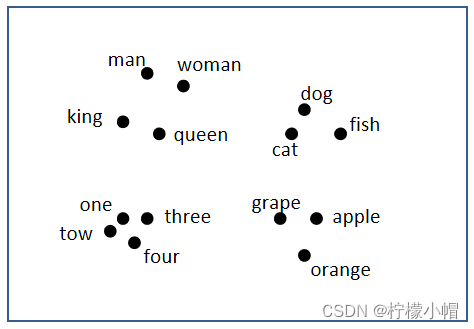
实际任务中,词汇量较大,表示维度较高,因此,我们不能手动为大型文本语料库开发词向量,而需要设计一种方法来使用一些机器学习算法(例如,神经网络)自动找到好的词嵌入,以便有效地执行这项繁重的任务。
3.6.2 词嵌入的优点
- 特征稠密;
- 能够表征词与词之间的相似度;
- 泛化能力更好,支持语义计算。
这篇关于Python 全栈体系【四阶】(五十八)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








