本文主要是介绍连续状态方程的离散化例子,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
连续状态方程的离散化
在控制系统中,连续状态方程的离散化是一个重要的步骤,用于将连续时间系统转换为离散时间系统,以便在数字控制器中实现。这通常涉及将连续时间的微分方程转换为离散时间的差分方程。常用的离散化方法
- 前向欧拉法(Forward Euler)简单易实现,但精度较低
- 后向欧拉法(Backward Euler)相对稳定,但计算复杂度较高
- 双线性变换(Tustin 变换)在精度和稳定性之间取得了平衡
运行上述代码后,你将得到连续时间系统离散化后的状态矩阵和输入矩阵。通过这些离散化方法,可以将连续时间系统转换为离散时间系统,以便在数字控制器中实现控制算法。这三种离散化方法各有优缺点,选择合适的方法取决于具体的应用场景和系统特性。
连续状态方程
假设我们有一个连续时间系统的状态方程:
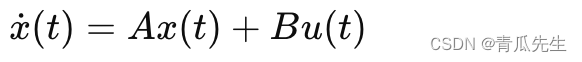
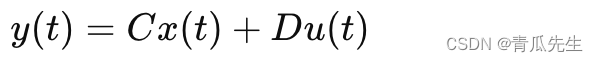
其中:
- x(t) 是状态向量
- u(t) 是输入向量
- y(t) 是输出向量
- A 是状态矩阵
- B 是输入矩阵
- C 是输出矩阵
- D 是直通矩阵
离散化方法
1. 前向欧拉法
这篇关于连续状态方程的离散化例子的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!