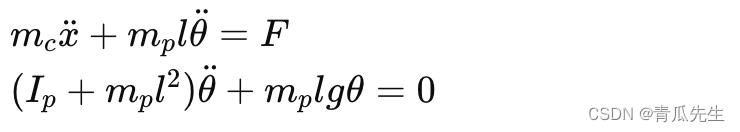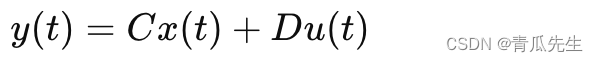状态方程ABCD矩阵如何确定 确定状态空间表示中的状态矩阵A、输入矩阵 B、输出矩阵C 和直通矩阵D，需要从系统的动力学方程出发，并将其转换为状态方程的形式。我们可以通过一个具体的物理系统（如倒立摆系统）来说明这一过程 例子：倒立摆系统 系统描述 考虑一个倒立摆系统，其中一个质量 m 被安装在一个长度为 l 的杆的末端。摆的底部固定在一个可移动的推车上。系统的状态变量包括推车的位置 x、推

连续状态方程的离散化 在控制系统中，连续状态方程的离散化是一个重要的步骤，用于将连续时间系统转换为离散时间系统，以便在数字控制器中实现。这通常涉及将连续时间的微分方程转换为离散时间的差分方程。常用的离散化方法 前向欧拉法（Forward Euler）简单易实现，但精度较低后向欧拉法（Backward Euler）相对稳定，但计算复杂度较高双线性变换（Tustin 变换）在精度和稳定性之间取得了

偶然看到的，原文：你看见蝴蝶翅膀上的数学公式了吗？——哆嗒数学网 看到matlab代码代码就像用麦酱改写一下试试。。 原matlab代码： f=@(t,x)[-8/3*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)];t_final=100;x0=[0;0;1e-10];[t,x]=ode45(f,[0,t_final],x0

当初学了信号与系统，微分方程，极点零点这些感觉还是很有用的。还有状态方程，输出方程。这些学了之后再看卡尔曼滤波都好些。中科院考信号与系统是有道理的。 来分析动态系统等等什么的，是有用的。   动态系统基本就是微分方程，你也可以写成积分方程，但是一般都两边求导成微分方程进行求解。   我现在很想重新拿起灰虎的书。   还有方浩的算子法。

题目：点击打开链接 题目大意：V个村庄，P个邮局，邮局建在村庄上，求一种建法，让V个村庄到最近邮局的距离最小 dp[i][j]:表示在1~i个村庄中建j个邮局时的路径最小值  m[i][j]:表示从i到j只建立一个邮局的路径的最小值 若从第i个村庄到第j个村庄只选取一个作为邮局的话则选择第(i+j)/2个 一开始我没懂，直到自己画了个图，假设把在5建的邮局移到4，则其他村庄的距离变化如图