蓝桥杯软件赛Java研究生组/A组）第二章基础算法-第三节：倍增

本文主要是介绍蓝桥杯软件赛Java研究生组/A组）第二章基础算法-第三节：倍增，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一：概述

倍增算法：是一种优化算法，通常应用在某些需要高效计算指数幂的场景。它基于分治的思想，通过反复求平方来实现快速计算指数幂的目的。通常应用在最近公共祖先问题、二分查找等等

二：典型题目

（1）题目一（快速幂）

倍增算法最经典的应用就是快速幂，快速幂算法是一种高效计算大整数幂的方法。如下快速幂计算$a^b$

• 当$b$为偶数时

$$a^b=a^{\frac{b}{2}}\ast a^{\frac{b}{2}}=(a^2{)}^{\frac{b}{2}}$$

• **当$b$为奇数时

$$a^b=a\ast a^{\frac{b}{2}}\ast a^{\frac{b}{2}}=a\ast (a^2{)}^{\frac{b}{2}}$$

**$\frac{b}{2}$向下取整，迭代求解，直到$b$为0为止

public static long qmi(long a, long b, long p) {long res = 1;  // 初始化结果为 1while (b > 0) {  // 当指数 b 大于 0 时执行循环if (b & 1 == 1) {  // 判断指数 b 的最低位是否为 1res = res * a % p;  // 如果最低位为 1，则将底数 a 的当前幂乘到结果中，并取模 p}a = a * a % p;  // 底数 a 自乘，相当于计算 a^2, a^4, a^8, ...b >>= 1;  // 将指数 b 右移一位，相当于将指数减半}return res;  // 返回结果
}

例如计算$2^{13}$

• $res=2,a=2^2,b=6$

• $res=2,a=2^4,b=3$

• $res=2^5,a=2^8,b=1$

• $res=2^{13},a=2^{16},b=0$

• 倍增一般会和其他算法结合使用

（2）题目二（ST表求区间最值）

思路：见ST表第二节：ST表

int[] arr; // 给定的array
int n = arr.length;// 预处理log数组，log[i]表示不大于i的最大二进制幂的指数
int[] log = new int[n+1];
log[1] = 0;
for(int i = 2; i <= n; i++) {
log[i] = log[i/2] + 1;
}// 初始化ST表，st[i][j]表示从位置i开始，长度为2^J的区间的最值
int[][] st = new int[n][log[n]+1];
for(int i = 0; i < n; i++) {
st[i][0] = arr[i]; // 长度为1的区间的最值就是其本身
}// 动态规划填表
for(int j = 1; j <= log[n]; j++) {
for(int i = 0; i + (1<<j) <=n; i++) {
st[i][j] = Math.max(st[i][j-1], st[i+(1<<(j-1))][j-1]);
}
}// 查找区间[L,R]的最值
int k = log[R-L+1];
// 这两个区间为：[L, L+2^k-1]和[R-2^K+1,R]return Math.max(st[L, k], st[R-(1<<j)+1][k])

（3）题目三（最近公共祖先）

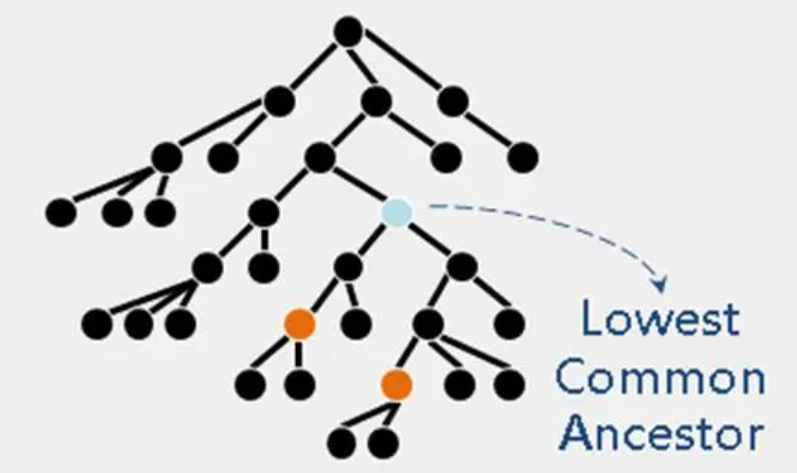
void dfs(int x, int u) {dep[x] = dep[u] + 1;// 设置当前节点的深度father[x][0] = u; // 直接父节点// 倍增法处理向上父节点for(int i = 1; i <= 20; i++) {father[x][i] = father[father[x][i-1]][i-1];}// 递归for(int y: list[x]) {if (y != u)dfs(y, x)}
}int lca(int x, int y) {// 确保x是更深的节点if (dep[x] < dep[y]) {swap(x, y);}// x向上跳，使x和y在同一深度for(int i = 20; i >= 0; i--) {if(dep[father[x][i]]>=dep[y]) {x = father[x][i];}}// 如果x和y相等，则找到了lcaif (x == y)return x;// 否则，同时开始向上跳，寻找for(int i = 20; i >= 0; i--) {if(father[x][i] != father[y][i]) {x = father[x][i];y = father[y][i];}}// 返回return father[x][0];
}int n; // 节点数量
List<Integer>[] list = new List[n+1]; // 邻接表
for(int i = 0; i <= n; i++) {list[i] = new ArrayList<>();
}
int[] dep = new int[n+1]; // 每个节点的深度
int[][] father = new int[n+1][21]; // 倍增法，father[x][i]存储x的2^i父节点// 深度搜索，初始化dep数组和father数组
dfs(1, 0);
// 求解x和y的lca
lca(x, y)

这篇关于蓝桥杯软件赛Java研究生组/A组）第二章基础算法-第三节：倍增的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---