MOOC 数据结构 | 7. 图（中）

本文主要是介绍MOOC 数据结构 | 7. 图（中），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最短路径问题

最短路径问题的抽象

在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径
- 这条路径就是两点之间的最短路径（Shortest Path）
- 第一个顶点为源点（Source）
- 最后一个顶点为终点（Destination）

问题分类

单源最短路径问题：从某固定源点触发，求其到所有其他顶点的最短路径、

□ （有向) 无权图

□ （有向) 有权图

多源最短路径问题

无权图的单源最短路算法

按照递增(非递减）的顺序找出各个顶点的最短路

BFS!

该过程是从v3开始，先访问的是v3的邻接点，之后每次都是访问上一个顶点的邻接点。这个过程和BFS类似，但又不完全相同。

void BFS(Vertex S)
{
~~visited[S] = true;~~
Enqueue(S, Q);
while(!IsEmpty(Q)) {
V = Dequeue(Q);
for ( V的每个邻接点W)
if (~~!visited[W]~~) {
~~visited[W] = true;~~
Enqueue(W, S);
}
}
}

void Unweighted(Vertex S)
{
Enqueue(S,Q);
while(!IsEmpty(Q)) {
V = Dequeue(Q); //distp[V]已经获取了
for(V的每个邻接点W)
if(dist[W] == -1) { //W没有被访问过
dist[W] = dist[V] + 1; //dist[W]的距离就是上一个顶点V + 1
path[W] = V; //S到W的必经点，就是W的前一个顶点V
Enqueue(W,Q);
}
}
} ${\color{Red} T=O(\left | V \right | + \left | E \right |)}$

在计算最短距离时，不需要visited[ ]，但是需要记录距离,dist数组初始化为一个负数或无意义的其他数，则当dist中的数等于该数时，则表示该顶点没有被访问过：（定义如下两个个数组）

dist[W] = S到W的距离

dist[S] = 0

path[W] = S到W的路径上经过的某顶点

Unweighted函数中记录path数组的作用：如要打印S到W的路径，先看path[W]为多少，它一定是前一个顶点，再看path[V]，就是V前一个顶点；于是可以顺着path数组一个一个向前推，推到源点，得到W到S的路径，将反向推的路径压入堆栈（堆栈起反序的作用），再从S开始一个一个出栈，就得到了S到W的路径。

时间复杂度：(假设用的邻接表 ) ${\color{Red} T=O(\left | V \right | + \left | E \right |)}$ ，因为在算法执行过程中，每个顶点Enqueue一次，Dequeue一次，所以涉及到2V，for是将每条边(E)访问一次。

那么究竟整个算法是怎么工作的呢？

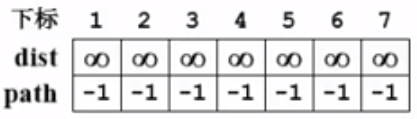
首先对数组dist和path进行初始化，都初始化为-1：

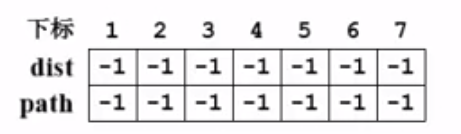
取图中的v3为源点，那么dist[3] = 0：

以上完成了初始化。接下来开始调用Unweighted函数：

1、因为源点为v3，所以调用Unweighted(3)：

根据Unweighted函数的执行过程，v3先入队：

然后执行while循环，判断队列是否为空，不为空，就将队列中的元素v3出队：

然后检查v3的邻接点（v1和v6），先看v1即dist[1] == -1？发现是的，于是dist[1] = dist[3] + 1 = 1, path[1] = 3，并将v1入队：

接着考虑下一个邻接点v6，v6也没有被访问过，所以更新dist[6]和path[6]，并将v6入队：

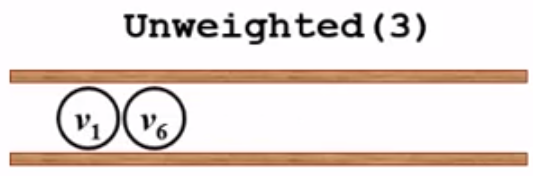
到此，对v3完成了操作。for循环结束，回到while循环继续执行。

2、此时队列不为空，要出队v1，

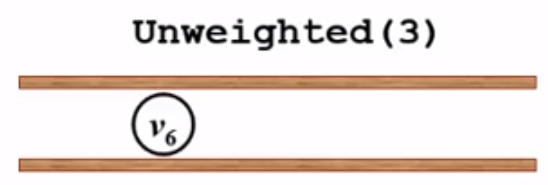
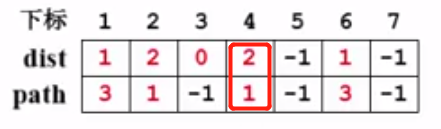
考察v1的邻接点（v2，v4），先看v2没有被访问过，于是更新dist[2] = dist[1] + 1 = 2和path[2] = 1，并将v2入队：

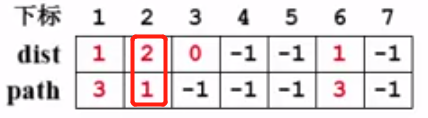(其中的dist[2] = 2的意思是v2到v3的最短距离是2，v2到v3的最短距离是经过v1完成的。）

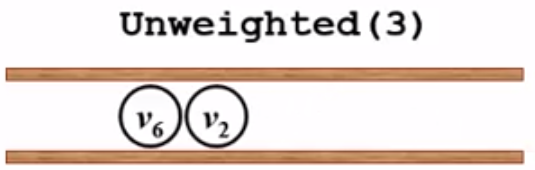
接下来考虑v4，类似地过程-更新dist[4] = dist[1] + 1 = 2，path[4] = 1，v4入队：

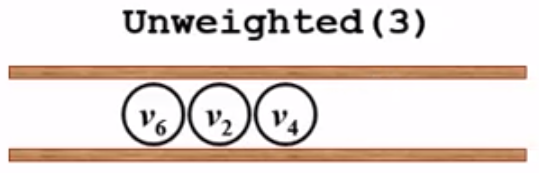
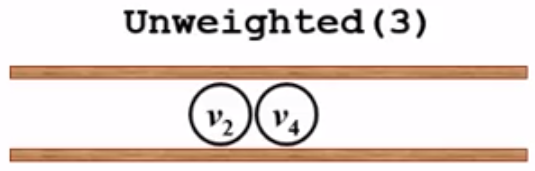
3、又回到while循环，此时队列不为空，于是标记一下v6，v6出队，而v6没有邻接点，所以for循环不会执行，直接又回到while循环。

4、队列不为空，v2出队，

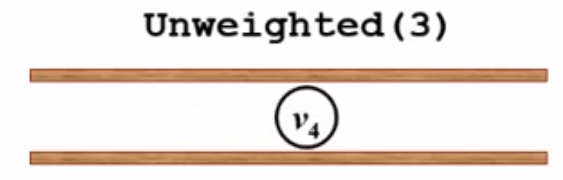
v2的邻接点有两个v4和v5,而v4的dist[4] = 2，所以v4已经得到了它的最短距离，就不需要改变了；继续看一下v5，dist[5] = -1，所以更新dist[5] = dist[2] + 1，path[5] = 2, v5进队：

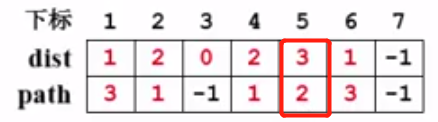
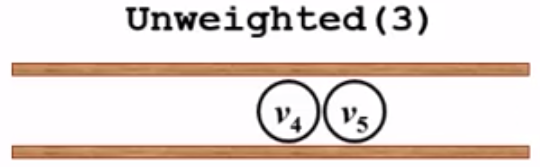
5、队列不为空，出队v4，v4有四个邻接点：v3，v5，v6，v7。其中v3，v5，v6都已经被访问过。只有v7没有被访问过，根据v4的距离向外扩展一步，更新dist[7]和path[7]，并将v7入队：

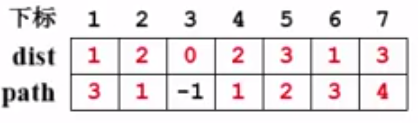
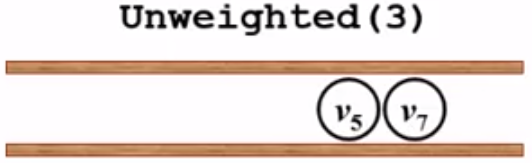
6、标记一下v5，出队v5，v5只有一个邻接点v7，而v7已经被被访问过，所以什么都不做，回去到while循环

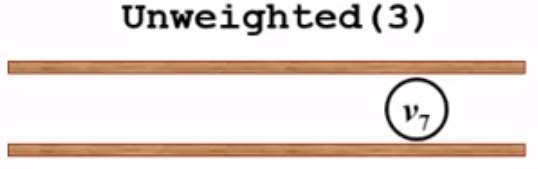
7、出队v7，而其他顶点都被访问过，再回到while循环

8、此时队列为空，所以程序结束。

dist数组中存储的是每一个顶点到v3的最短距离。

如果要求输出v3到v7的最短路径，做法是：

（1）从path[7]开始，发现path[7] = 4, 意思是最短路径是从v4到达的v7；

（2）再追踪path[4]，而path[4] = 1，意思是最短路径是从v1到到达的v4；

（3）跟踪path[1]，path[1]= 3,意思是最短路径是从v3到到达的v1；

（4）跟踪path[3]，发现path[3] = -1, 小于0，意味着v3就是源点。

（5）所以v3到v7的最短路径就是v3->v1->v4->v7

源码

/* 邻接表存储 - 无权图的单源最短路算法 *//* dist[]和path[]全部初始化为-1 */
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{Queue Q;Vertex V;PtrToAdjVNode W;Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */dist[S] = 0; /* 初始化源点 */AddQ (Q, S);while( !IsEmpty(Q) ){V = DeleteQ(Q);for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */if ( dist[W->AdjV]==-1 ) { /* 若W->AdjV未被访问过 */dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */AddQ(Q, W->AdjV);}} /* while结束*/
}

有权图的单源最短路算法

1、

（v1选做源点，v6选做终点）

（最短路径是v1->v4->v7->v6）

可以发现有权图的最短路径不一定是经过的顶点数最少的路径。

2、

（v5为源点，v4为终点，而权重表示路上的花费，那么-10表示不但不花费，还会得到钱）

要求v5到v4花销最小，那么沿着v5->v4->v2->v5这个路径不断绕圈，就能得到无穷大的钱（每一次都会有2 +3 -10 = -5，即5元的收入）。

如果图里有负值圈，那么算法就会挂掉。后续的讲解不考虑这种情况。

有权图最短路算法也是：按照递增的顺序找出各个顶点的最短路

解决有权图最短路算法有一个名称：

Dijkstra算法

令S = {源点s + 已经确定了最短路径的顶点 $v_i$ }
对任一未收录的顶点v，定义dist[v] 为s到v的最短路径长度，但该路径仅经过S中的顶点。即路径{ $s\rightarrow (v_i \epsilon S)\rightarrow v$ }的最小长度
若路径是按照递增(非递减）的顺序生成的，则
- 真正的最短路必须只经过S中的顶点
- 每次从未收录的顶点中选一个dist最小的收录（贪心）
- 增加一个v进入S，可能影响另一个w的dist值！ ---(如果v加入到S后，w的dist值变小，那么v一定在路径上，v到w一定有一条直接的边，即w一定是v的邻接点，v加入后能影响的就是它的邻接点。)
  - dist[w] = min{ dist[w] , dist[v] + <v,w>的权重}

算法框架

void Dijkstra(Vertex s)
{while(1) {V = 未收录顶点中dist最小者;if(这样的V不存在) //全部被收录break;collected[V] = true;for(V的每个邻接点W) if(collected[W] == false) {if(dist[V] + E<v,w> < dist[W]) {dist[W] = dist[V] + E<v,w>;path[W] = V;}}}
}
/*不能解决有负边的情况*/

这个算法的初始化：
1、dist[s] = 0
2、与s直接相连的初始化为权重
3、与s没有直接相连的初始化为+∞ （因为dist[V] + E<v,w> < dist[W] 才能进行更新）

时间复杂度

Dijstra算法的时间复杂度取决于是如何解决“dist[V] + E<v,w> < dist[W]”，同时也会确定“dist[W] = dist[V] + E<v,w>;”的更新方法。

方法1：直接扫描所有未收录顶点 -- O(|V|)
- T = O(|V|² + |E|) ----------- 对于稠密图(E = V²)效果好
方法2：将dist存在最小堆中 -- O(log|V|)
- 更新dist[w] 的值 -- O(log|V|)
- T = O(|V| log|V| + |E| log|V|） = O(|E| log|V|) ----对于稀疏图(E和V是相同数量级)效果好

算法流程

void Dijkstra(Vertex s)
{while(1) {V = 未收录顶点中dist最小者;if(这样的V不存在) //全部被收录break;collected[V] = true;for(V的每个邻接点W) if(collected[W] == false) {if(dist[V] + E<v,w> < dist[W]) {dist[W] = dist[V] + E<v,w>;path[W] = V;}}}
}

1、调用Dijstra算法之前，要进行初始化：

这个例子中选择v1作为源点，于是相应的，dist[1] = 0，同时v1的邻接点（v1和v4）到源点的最短距离就是边的权重，于是v2到源点的距离更新为2，path[2] = 1；邻接点v4，dist[4] = 1，path[4] = 1。

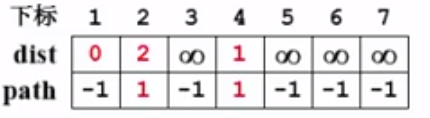
至此，初始化完成。

2、开始执行Dijstra算法：

传入v1，接着要从未收录的顶点中选择dist最小的，无论使用扫描还是最小堆，v1因为是源点，不算；发现v4最小，所以V = v4，collcted[4] = true，表示访问过。

v4的邻接点：v3，v5，v6，v7。

先看v3，v3还没被收录，判断dist[3] = +∞，而dist[V] + E<v,w> = dist[4] + E<4,3> = 1 + 2 =3，是小于+∞的，所以这条路径是当前从v1到v3的最短路。更新dist[3] = 3, path[3] = 4。

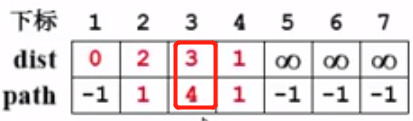
再来看v5，同v3的过程：

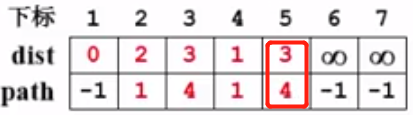
同样处理v6和v7：

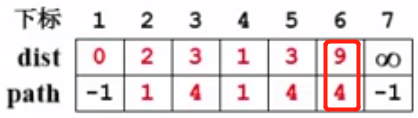
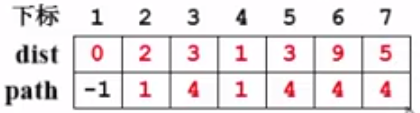
至此，v4的邻接点就处理完毕了。接下来进入下一次循环。

3、未收录顶点中dist最小者，现在是v2,所以标记v2，V = 2，collected[2] = true，对v2的邻接点v4和v5进行处理。

v4：已经被访问过，所以不做处理；

v5：dist[V] + E<v,w> = dist[2] + E<2,5> = 2 + 10 =12 大于dist[W] =dist[5] = 3。所以保持v5的值，不做处理。

至此，v2的邻接点就处理完毕了。进入下一次循环

4、未收录的顶点中dist最小者，这次有两个候选：v3和v5，随便挑一个，选择v3，collected[3] = true。

v3的邻接点：v1和v6。

先看v1：已经访问过。

再看v6：当前dist[6] = 9，是从v1->v4->v6; 那么从v3走会怎样呢？从v1到v3（v1->v4->v3）是3，v3->v6是5，所以整个路径的长度为8，比现在的9要小一点。即不等式dist[V] + E<v,w> = dist[3] + E<3,6> = 3+ 5 =8 < dist[6] = 9，所以更新dist[6]和path[6]:

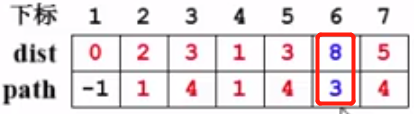
至此，结束了对v3的处理。

5、继续来找未收录顶点中dist最小的，现在是v5，collected[5] = true。

v5的邻接点只有v7。

当前dist[7] = 5；而dist[5] + E<5,7> = 3 + 6 = 9大于5，所以不等式不成立，不做处理。

6、在未收录的结点中还有v6和v7，现在v7的dist较小，所以collected[7] = true。

而v7唯一的邻接点就是v6。

现在dist[6] = 8，而dist[7] + E<7,6> = 5 + 1 = 6小于8，所以不等式成立，更新dist[6]和path[6]：

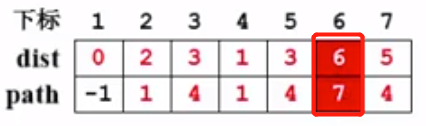
7、还剩v6没有被收录，collected[6] = true。因为v6没有邻接点，所以不做处理。

8、再找没有被收录的顶点，发现不存在，所以break结束程序。

如果要问v1到v6的最短路径是哪条，处理过程同无向图的处理过程：

（1）从v6开始，发现v7是它的上一个顶点，即最短路径是v7->v6；

（2）跟踪path[7] = 4，即最短路径是从v4->v7；

（3）跟踪path[4] = 1,即是从v1->v4;

（4）跟踪path[1] = -1，即v1是源点。

（5）所以最短路径就是v1->v4->v7->v6。

源码

* 邻接矩阵存储 - 有权图的单源最短路算法 */Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */Vertex MinV, V;int MinDist = INFINITY;for (V=0; V<Graph->Nv; V++) {if ( collected[V]==false && dist[V]<MinDist) {/* 若V未被收录，且dist[V]更小 */MinDist = dist[V]; /* 更新最小距离 */MinV = V; /* 更新对应顶点 */}}if (MinDist < INFINITY) /* 若找到最小dist */return MinV; /* 返回对应的顶点下标 */else return ERROR;  /* 若这样的顶点不存在，返回错误标记 */
}bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{int collected[MaxVertexNum];Vertex V, W;/* 初始化：此处默认邻接矩阵中不存在的边用INFINITY表示 */for ( V=0; V<Graph->Nv; V++ ) {dist[V] = Graph->G[S][V];if ( dist[V]<INFINITY )path[V] = S;elsepath[V] = -1;collected[V] = false;}/* 先将起点收入集合 */dist[S] = 0;collected[S] = true;while (1) {/* V = 未被收录顶点中dist最小者 */V = FindMinDist( Graph, dist, collected );if ( V==ERROR ) /* 若这样的V不存在 */break;      /* 算法结束 */collected[V] = true;  /* 收录V */for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W *//* 若W是V的邻接点并且未被收录 */if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {if ( Graph->G[V][W]<0 ) /* 若有负边 */return false; /* 不能正确解决，返回错误标记 *//* 若收录V使得dist[W]变小 */if ( dist[V]+Graph->G[V][W] < dist[W] ) {dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */path[W] = V; /* 更新S到W的路径 */}}} /* while结束*/return true; /* 算法执行完毕，返回正确标记 */
}

多源最短路算法

方法1：直接将单源最短路算法调用|V|遍
- T = O(|V|³ + |E| x |V|) ------对于稀疏图效果好
方法2：
- T = O(|V|³）------对于稠密图效果好

Floyd算法

$D^{k}[i][j] =$ 路径 $\left \{ i\rightarrow \left \{ l \leq k \right \} \rightarrow j\right \}$ 的最小长度
$D^{0},D^{1},...,D^{|V|-1}[i][j]$ 即给出了 i 到 j 的真正最短距离
最初的是什么？（即初始矩阵）
- 答：定义为邻接矩阵，对角线全是0；i和j之间如果有边，D[i][j]就定义为这条边的权重；没有直接的边相连的时候，D[i][j]初始化为+∞
当已经完成，递推到时：
- 或者k∉最短路径 $\left \{ i\rightarrow \left \{ l \leq k \right \} \rightarrow j\right \}$ ，则 $D^{k} = D^{k-1}$
- 或者k∈最短路径 $\left \{ i\rightarrow \left \{ l \leq k \right \} \rightarrow j\right \}$ ，则该路径必定由两段最短路径组成： $D^{k}[i][j] = D^{k-1}[i][k] + D^{k-1}[k][j]$

算法程序

void Floyd()
{for(i = 0; i < N; i++)for(j = 0; j < N; j++) {D[i][j] = G[i][j];path[i][j] = -1;}for(k = 0;k < N;k++) for(i = 0; i < N; i++)for(j = 0; j < N; j++)if(D[i][k] + D[k][j] < D[i][j]) {D[i][j] = D[i][k] + D[k][j];path[i][j] = k;}}

如果要打印i到j的最短路径，那么这个最短路径一定是由"i到k的最短路径 + k + k到j的最短路径"。所以可以递归地打印i到k的路径，把path[i][j]的值打印出来，再递归地打印k到j的路径。

时间复杂度

三重循环，T = O(N³）

源码

/* 邻接矩阵存储 - 多源最短路算法 */bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{Vertex i, j, k;/* 初始化 */for ( i=0; i<Graph->Nv; i++ )for( j=0; j<Graph->Nv; j++ ) {D[i][j] = Graph->G[i][j];path[i][j] = -1;}for( k=0; k<Graph->Nv; k++ )for( i=0; i<Graph->Nv; i++ )for( j=0; j<Graph->Nv; j++ )if( D[i][k] + D[k][j] < D[i][j] ) {D[i][j] = D[i][k] + D[k][j];if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */return false; /* 不能正确解决，返回错误标记 */path[i][j] = k;}return true; /* 算法执行完毕，返回正确标记 */
}

这篇关于MOOC 数据结构 | 7. 图（中）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！