MOOC 数据结构 | 4. 树（中）

2024-06-06 19:08
文章标签 数据结构 mooc

本文主要是介绍MOOC 数据结构 | 4. 树（中），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 什么是二叉搜索树

查找问题：

  • 静态查找与动态查找
  • 针对动态查找，数据如何组织？

二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：

  1. 非空左子树的所有键值小于其根结点的键值。
  2. 非空右子树的所有键值大于其根结点的键值。
  3. 左、右子树都是二叉搜索树。

：不是二叉搜索树，对于结点10来说，其右子树应该比10大。

：是二叉搜索树。

：是二叉搜索树。

2. 二叉搜索树操作的特别函数

2.1 二叉搜索树的查找操作：Find

  • 查找从根结点开始，如果树为空，返回NULL
  • 若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：
  1. 若X小于根结点键值，只需在左子树中继续搜索；
  2. 如果X大于根结点的键值，在右子树中进行继续搜索；
  3. 若两者比较结果是相等，搜索完成，返回指向此结点的指针。

Position Find(ElementType X, BinTree BST)
{if (!BST) return NULL;  /*查找失败*/if(X > BST->Data)return Find(X, BST->Right);  /*在右子树中继续查找*/else if (X < BST->Data)return Find(X, BST->Left);   /*在左子树中继续查找*/else /*X == BST->Data*/return BST;  /*查找成功，返回结点的找到结点的地址*/
}

递归实现的效率较低，且都是“尾递归”（尾递归就是在程序要返回的时候进行递归），从编译角度来讲，“尾递归”都可以用循环来实现。

□ 由于非递归函数的执行效率高，可将“尾递归”函数改为迭代函数

Position Find(ElementType X, BinTree BST)
{ while( BST ) {if(X > BST->Data)   BST = BST->Right;   /*向右子树中移动，继续查找*/else if (X < BST->Data)BST = BST->Left;    /*向左子树中移动，继续查找*/else   /*X == BST->Data*/return BST;   /*查找成功，返回结点的找到结点的地址*/}return NULL; /*查找失败*/ 
}

查找效率决定于树的高度  ---- 树不要往一边倒，只有左子树或右子树，所有结点链成一条链，高度就是n - 1。所以就会引入后面讲的平衡二叉树。

2.2  查找最大和最小元素

□ 最大元素一定是在树的最右分枝的端结点上

□ 最小元素一定是在树的最左分枝的端结点上

//查找最大元素的递归函数
Position FindMax(BinTree BST)
{if (!BST)  return NULL;else if(!BST->Right)return BST;else return FindMax(BST->Right);
}//查找最大元素的迭代函数：
Position FindMax(BinTree BST)
{if(BST){while(BST->Right)BST = BST->Right;  /*沿右分支继续查找，直到右子树为空*/}return BST;
}
//查找最小元素的递归函数：
Position FindMin(BinTree BST)
{if (!BST) return NULL;   /*空的二叉搜索树，返回NULL*/else if (!BST->Left)return BST;  /*找到最左叶结点并返回*/elsereturn FindMin(BST->Left);  /*沿左分支继续查找*/
}
//查找最小元素的迭代函数
Position FindMin(BinTree BST)
{if( BST ){while(BST->Left)BST = BST->Left;}return BST;
}

2.3 二叉搜索树的插入

【分析】关键是要找到元素应该插入的位置（要保证插入完毕后这棵树还是二叉搜索树），可以采用与Find类似的方法。

1. 要插入35，先与根结点进行比较（35 > 30），所以就往右走。

2.与41进行比较（35 < 41），所以就往左边走。

3. 与33比较（35 > 33），就往右走，发现右边是空的，于是就进行插入。

4. 插入35。

二叉搜索树的插入算法：

BinTree Insert(ElementType X, BinTree BST)
{if (!BST){/*若原树为空，生成并返回一个结点的二叉搜索树*/BST = malloc(sizeof(struct TreeNode));BST->Data = X;BST->Left = BST->Right = NULL;}else /*开始找要插入元素的位置*/{if(X < BST->Data)BST->Left = Insert(X, BST->Left); /*递归插入左子树*/else if (X > BST->Data)BST->Right = Insert(X, BST->Right);  /*递归插入右子树*//*else X已经存在，什么都不做*/}return BST;
}

上面的if ( !BST )分支执行的时机：BST指向33结点时，再进行递归，BST->Right = NULL，就申请空间构造一个结点并返回。

即是BST->Right = Insert(X, BST->Right); 中insert结果返回了，返回的结果就赋值给了BST->Right，也就是：

【例】以一年十二个月的英文缩写为键值，按从一月到十二月顺序输入，即输入序列为(Jan, Feb, Mar, Apr, May, Jun, July, Aug, Sep, Oct, Nov, Dec)   

这里的大小指键值的英文字典序。

2.4 二叉搜索树的删除

□ 考虑三种情况：

  • ①要删除的是叶结点：直接删除，并再修改其父结点指针---置为NULL

【例】删除35

先要找到35，然后再删除，最后将33的右结点置为NULL

  • ②要删除的结点只有一个孩子结点：将其父结点的指针指向要删除结点的孩子结点

【例】删除33

先要找到33（查找过程），然后将35挂在41的左边即可：

--->  

  • ③要删除的结点有左、右两棵子树：用另一结点替代被删除结点：右子树的最小元素 或者 左子树的最大元素

【例】删除41

（1）取右子树中的最小元素替代

-->  

(2) 取左子树中的最大元素替代

-->

无论左子树的最大值还是右子树的最小值，都只有一个儿子。

BinTree Delete(ElementType X, BinTree BST)
{Position Tmp;if (!BST) printf("要删除的元素未找到");else if (X < BST->Data)BST->Left = Delete(X, BST->Left);   /*左子树递归删除，Delete返回的是删除后的左子树的根结点地址，然后赋值给Left*/else if (X > BST->Data)BST->Right = Delete(X, BST->Right); /*右子树递归删除*/else  /*找到要删除的结点*/if (BST->Left && BST->Right)  /*被删除结点有左右两个子结点*/{Tmp = FindMin(BST->Right);  /*在右子树中找最小元素填充删除结点*/BST->Data = Tmp->Data;BST->Right = Delete(BST->Data, BST->Right); /*在删除结点的右子树中删除最小元素*/}else  /*被删除结点有一个或无子结点*/{Tmp = BST;if (!BST->Left)  /*有右孩子或无子结点*/BST = BST->Right;else if (!BST->Right)  /*有左孩子或无子结点*/BST = BST->Left;free(Tmp);}return BST;
}

3. 什么是平衡二叉树

【例】搜索树结点不同插入次序，将导致不同的深度和平均查找长度ASL

按照“字典顺序”比较大小

"平衡因子"（Balance Factor，简称BF）：BF(T）= {\color{Blue} h_L-h_R}，其中h_L和h_R分别为T的左、右子树的高度。

(AVL是提出该概念的科学家名字的缩写）

1. （对于结点4来说，左右子树的高度差为0，是平衡的；但是对于结点3来说，左子树高度为2，右子树高度为0，所以高度差为2，是不平衡的。所以这棵树不是平衡树）。

2. 

3. （对于结点7来说，左右子树的高度差为2，所以不是平衡二叉树）

3.1 平衡二叉树的高度能达到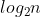log_2n吗？

设n_h高度为h的平衡二叉树的最少结点数（此处的高度为边的条数）。结点数最少时：

所以当高度为h的时候，结点数最少无非是下面两种情况：

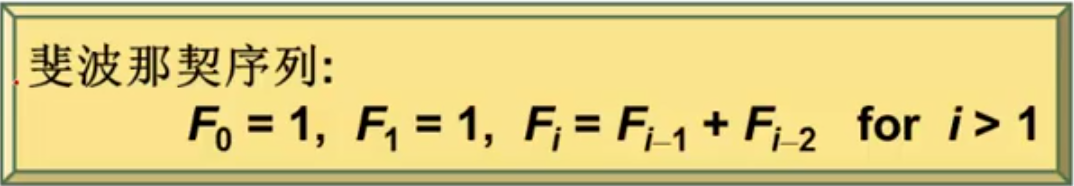
通过与斐波那契序列的关系比较：

可以得出n_h与h是指数关系。进一步得出结论：

4.平衡二叉树的调整

4.1 RR旋转

插入顺序：Mar、May、Nov

1、一开始只有Mar，Mar结点的平衡因子为0

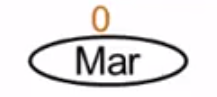
2、来了May，

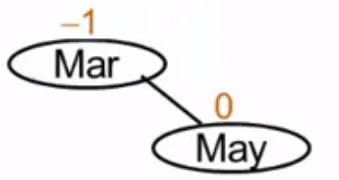
3、来了Nov

可以看到Mar结点的平衡因子为-2，所以这不是一棵平衡二叉树。因此就要调整：

概括一下，是如下的这种模式：

 

一开始是一棵平衡二叉树，在B的右子树上又插入了一个结点，所以A结点就不平衡了，因为插入的结点在A的右子树的右子树上，所以进行RR旋转，将B放到A的位置，A链接到B的左边，A_L还是链接在A的左子树上，而因为还是一棵二叉搜索树，B_L比B小，比A大，所以链接到A的右边。

实例1：如下树上插入结点15

这就导致了结点5不平衡，二者的关系是破坏者在被破坏者的右子树的右子树上，所以进行RR旋转：

视频讲解过程：链接：https://pan.baidu.com/s/11gV-yFijp2ivB714flTLHw  提取码：s6eu 
 

实例2：插入结点13

       

破坏者也是在被破坏者的右子树的右子树上，所以也是RR旋转：

4.2 LL旋转

、

插入结点Apr之后，Mar结点不平衡了，破坏者在被破坏者的左子树的左子树上，所以，进行对Apr、Aug和Mar结点进行LL旋转。可以看到，旋转并不一定是发生在根结点上。

 

在A结点的左子树的左子树上插入了一个结点（可能在左边，可能在右边），导致了结点A不平衡，于是进行LL调整，将B结点置为根结点，被破坏者A作为右子树，B_R比B大，比A小，所以链接在A的左边。

4.3 LR旋转

原来有一棵平衡树：

插入结点Jan：

结点May不平衡了，破坏者（Jan）在被破坏者（May）的左子树的右子树上，所以进行LR旋转：

基本方法：重点关注May、Aug和Mar三个结点，将这三个结点调平衡。三者中，中间的值时Mar，所以这三个结点调成这样的状态：

4.4  RL旋转

插入结点Feb：

Aug结点的平衡性被破坏了，破坏者(Feb)在被破坏者(Aug)的右子树的左子树上，所以进行RL旋转：

基本模式就是把Aug、Jan和Dec三个结点进行调整：

四种模式如何判别，就看插入者把哪个结点破坏了，插入者与被破坏者之间的关系。

例子：

插入结点June：

破坏者（June）在被破坏者(Mar)的左子树的右子树上，所以进行LR旋转，即调整Mar、Dec和Jan三个结点：

再插入Oct：

破坏了结点May的平衡性，破坏者（Oct）在被破坏者(May）的右子树的右子树上，所以进行RR旋转：

再插入结点Sept:

是平衡的，虽然树结构没有变化，但是平衡因子是要变化的。

5. 小白专场：是否同一棵二叉搜索树

5.1 题目

04-树4 是否同一棵二叉搜索树 (25 分)

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式:

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。

简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式:

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例:

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例:

Yes
No
No

5.2 题意理解

□ 给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。

     ☆例如，按照序列{2, 1 ,3}和{2， 3， 1}插入初始为空的二叉搜索树，都得到一样的结果。

       

□问题：对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

对于输入样例：3 1 4 2 和 3 4 1 2 生成的二叉搜索树相同，所以输出Yes。

3 2 4 1 这个输入序列对应的二叉搜索树和 3 1 4 2 对应的二叉搜索树不同，所以输出No。

5.3 求解思路

两个序列是否对应相同搜索树的判别

1、分别建两棵搜索树的判别方法

          根据两个序列分别建树，再判别树是否一样（根、左子树、右子树是不是一样，递归）

2、不建树的判别方法

两个序列的第一个数都是3，所以两棵树的根结点都是3，根据根结点3，可以将序列后面的数分为两堆--比3大，比3小，顺序还是按照原来的顺序。比较两个左子树是否一样，两个右子树是否一样。所以，这两棵搜索树是一样的：

来看另一组数据：

‘

显然，左子树不同（一个左子树根结点是1，一个左子树根结点是2），（采用递归）。

3、建一棵树，再判别其他序列是否与该树一致

  1. 搜索树表示
  2. 建搜索树T
  3. 判别一序列是否与搜索树T一致

5.3.1 搜索树表示

typedef struct TreeNode *Tree;
struct TreeNode
{int v;Tree Left, Right;int flag;   /*判别一个序列是否与树一致，结点访问标记*/
};

5.3.2 程序框架搭建

               

5.3.3 如何建搜索树

 

构造新结点：

    

插入结点：

   

代码：

Tree NewNode(int V)
{Tree T = (Tree)malloc(sizeof(struct TreeNode));T->v = V;T->Left = T->Right = NULL;T->flag = 0; //没被访问过的结点flag = 0,被访问过的结点flag = 1 return T;
}Tree Insert(Tree T, int V)
{if(!T)T = NewNode(V);else {if (V > T->v)T->Right = Insert(T->Right, V);else T->Left = Insert(T->Left, V);}return T;
}Tree NewNode(int V)
{Tree T = (Tree)malloc(sizeof(struct TreeNode));T->v = V;T->Left = T->Right = NULL;T->flag = 0; //没被访问过的结点flag = 0,被访问过的结点flag = 1 return T;
}Tree Insert(Tree T, int V)
{if(!T)T = NewNode(V);else {if (V > T->v)T->Right = Insert(T->Right, V);else T->Left = Insert(T->Left, V);}return T;
}

5.3.3 如何判别

对于上面的例子，比较过程：

序列（3 2 4 1）

①先看3，是T的根结点，将flag标记为1；

②接下来找2，为了找2，要从3开始找，比较过程就是树中的3 -> 1 ->2，3此前碰到过，而1没有碰到过。因此可以判定，序列与树不一致。

 

bug在于比如序列3 2 4 1，比较到1的时候发现与T不一致，此时就直接return，然后进入下一个序列的比较，该序列中的4 1 会被当做下一个序列的数。所以发现不一致的时候不能立即return，要把这个序列后面的数都读完。

另外两个小的函数ResetT和FreeTree：

void ResetT(Tree T)  /*清除T中各结点的flag标记*/
{if(T->Left)ResetT(T->Left);if(T->Right)Reset(T->Right);T->flag = 0;
}void FreeTree(Tree T)  /*释放T的空间*/
{if (T->Left)FreeTree(T->Left);if(T->Right)FreeTree(T->Right);free(T);
}

5.3.4 完整代码

#include <stdio.h>
#include <stdlib.h>typedef struct TreeNode *Tree;
struct TreeNode
{int v;Tree Left, Right;int flag;   /*判别一个序列是否与树一致，结点访问标记*/
};Tree NewNode(int V)
{Tree T = (Tree)malloc(sizeof(struct TreeNode));T->v = V;T->Left = T->Right = NULL;T->flag = 0; //没被访问过的结点flag = 0,被访问过的结点flag = 1return T;
}Tree Insert(Tree T, int V)
{if(!T)T = NewNode(V);else{if (V > T->v)T->Right = Insert(T->Right, V);elseT->Left = Insert(T->Left, V);}return T;
}Tree MakeTree(int N)
{Tree T;int i, V;scanf("%d",&V);  //读入第一个数T = NewNode(V);  //为这个数构造一个结点，T中只包含了一个结点for(i = 1; i < N; i++){scanf("%d", &V);T = Insert(T, V);  //当前读入的数插入到结点中}return T;
}int check(Tree T, int V)
{if(T->flag){if(V < T->v)return check(T->Left, V);else if ( V > T->v)return check(T->Right, V);elsereturn 0; //序列中有重复出现的数，也作为不一致处理}else{if ( V == T->v){T->flag = 1;return 1;}elsereturn 0;}
}int Judge(Tree T, int N)
{int i, V, flag = 0;  /*flag：0表示目前还一致，1表示已经不一致*/scanf("%d", &V);if (V != T->v)   //判断树根是否相同flag = 1;elseT->flag = 1; //标记该结点已经访问过for(i = 1; i < N; i++){scanf("%d", &V);if((!flag) && (!check(T, V)))  //如果flag = 1，即已经不一致了，就不用check了，直接继续读下一个flag = 1;}if(flag)return 0;elsereturn 1;
}void ResetT(Tree T)  /*清除T中各结点的flag标记*/
{if(T->Left)ResetT(T->Left);if(T->Right)ResetT(T->Right);T->flag = 0;
}void FreeTree(Tree T)  /*释放T的空间*/
{if (T->Left)FreeTree(T->Left);if(T->Right)FreeTree(T->Right);free(T);
}int main()
{int N,L,i;Tree T;scanf("%d", &N);while(N){scanf("%d", &L);T = MakeTree(N);for(i = 0; i < L;i++){if(Judge(T, N))printf("Yes\n");elseprintf("No\n");ResetT(T);}FreeTree(T); //一组数据处理完，要进入下一组数据前，要把当前的树Freescanf("%d", &N); //第二组输入}return 0;
}

PTA系统已关闭测试，输入样例测试Pass：

 

这篇关于MOOC 数据结构 | 4. 树（中）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1036976。

相关文章

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

8.3 交换排序 8.3.1 冒泡排序 【算法特点】 (1) 稳定排序。 (2) 可用于链式存储结构。 (3) 移动记录次数较多，算法平均时间性能比直接插入排序差。当初始记录无序，n较大时， 此算法不宜采用。 #include <stdio.h>#include <stdlib.h>#define MAXSIZE 26typedef int KeyType;typedef char In
阅读更多...
【408数据结构】散列 （哈希）知识点集合复习考点题目

【408数据结构】散列 （哈希）知识点集合复习考点题目

苏泽  “弃工从研”的路上很孤独，于是我记下了些许笔记相伴，希望能够帮助到大家    知识点 1. 散列查找 散列查找是一种高效的查找方法，它通过散列函数将关键字映射到数组的一个位置，从而实现快速查找。这种方法的时间复杂度平均为(
阅读更多...
浙大数据结构：树的定义与操作

浙大数据结构：树的定义与操作

四种遍历 #include<iostream>#include<queue>using namespace std;typedef struct treenode *BinTree;typedef BinTree position;typedef int ElementType;struct treenode{ElementType data;BinTree left;BinTre
阅读更多...
Python 内置的一些数据结构

Python 内置的一些数据结构

文章目录 1. 列表 (List)2. 元组 (Tuple)3. 字典 (Dictionary)4. 集合 (Set)5. 字符串 (String) Python 提供了几种内置的数据结构来存储和操作数据，每种都有其独特的特点和用途。下面是一些常用的数据结构及其简要说明： 1. 列表 (List) 列表是一种可变的有序集合，可以存放任意类型的数据。列表中的元素可以通过索
阅读更多...
浙大数据结构：04-树7 二叉搜索树的操作集

浙大数据结构：04-树7 二叉搜索树的操作集

这道题答案都在PPT上，所以先学会再写的话并不难。 1、BinTree Insert( BinTree BST, ElementType X ) 递归实现，小就进左子树，大就进右子树。 为空就新建结点插入。 BinTree Insert( BinTree BST, ElementType X ){if(!BST){BST=(BinTree)malloc(sizeof(struct TNo
阅读更多...
【数据结构入门】排序算法之交换排序与归并排序

【数据结构入门】排序算法之交换排序与归并排序

前言         在前一篇博客，我们学习了排序算法中的插入排序和选择排序，接下来我们将继续探索交换排序与归并排序，这两个排序都是重头戏，让我们接着往下看。  一、交换排序 1.1 冒泡排序 冒泡排序是一种简单的排序算法。 1.1.1 基本思想 它的基本思想是通过相邻元素的比较和交换，让较大的元素逐渐向右移动，从而将最大的元素移动到最右边。 动画演示： 1.1.2 具体步
阅读更多...
数据结构：线性表的顺序存储

数据结构：线性表的顺序存储

文章目录 🍊自我介绍🍊线性表的顺序存储介绍概述例子 🍊顺序表的存储类型设计设计思路类型设计 你的点赞评论就是对博主最大的鼓励 当然喜欢的小伙伴可以：点赞+关注+评论+收藏（一键四连）哦~ 🍊自我介绍   Hello,大家好，我是小珑也要变强（也是小珑），我是易编程·终身成长社群的一名“创始团队·嘉宾” 和“内容共创官” ,现在我来为大家介绍一下有关物联网-嵌入
阅读更多...
[数据结构]队列之顺序队列的类模板实现

[数据结构]队列之顺序队列的类模板实现

队列是一种限定存取位置的线性表，允许插入的一端叫做队尾（rear），允许删除的一端叫做队首（front）。 队列具有FIFO的性质 队列的存储表示也有两种方式：基于数组的，基于列表的。基于数组的叫做顺序队列，基于列表的叫做链式队列。 一下是基于动态数组的顺序队列的模板类的实现。 顺序队列的抽象基类如下所示：只提供了接口和显式的默认构造函数和析构函数，在派生类中调用。 #i
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2