MOOC 数据结构 | 1. 基本概念

本文主要是介绍MOOC 数据结构 | 1. 基本概念，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.什么是数据结构

1.1：如何在书架上摆放图书？

方法1：随便放
- 操作1：新书怎么插入？
  - 哪里有空放哪里，一步到位！
- 操作2：怎么查找某本指定的书？
  - ......累死
方法2：按照书名的拼音字母顺序排放
- 操作1：新书怎么插入？
  - 新进一本《阿Q正传》.... (每本都要往后错位）
- 操作2：怎么找到某本指定的书？
  - 二分查找！
方法3：把书架划分成几块区域，每块区域指定摆放某种类别的图书；在每种类别内，按照书名的拼音字母顺序摆放
- 操作1：新书怎么插入？
  - 先定类别，二分查找确定位置，移出空位
- 操作2：怎么找到某本指定的书？
  - 先定类别，再二分查找
- 问题：空间如何分配？类别应该分多细？
  - 各种类别的书的藏书量不一样，每一种类的书架事先分好吗？书架多了，就有空间始终空着浪费；书架少了，进新书就会不断要加新柜子
  - 类别如果分得比较粗，那么同一类里面的书就有很多，工作量还是很大；如果分得特别细，带来的副作用就是类别太多

这个例子要说明的是：解决问题方法的效率，跟数据的组织方式有关。

1.2：写程序实现一个函数printN，使得传入一个正整数为N的参数后，能顺序打印从1到N的全部正整数

该问题可以用两种方法实现：循环和递归。

void printN(int N) //循环实现
{int i;for(i = 1; i <= N; i++){printf("%d\n", i);}return;
}void printN(int N) //递归实现
{if(N){printN(N-1);printf("%d\n", N);}return;
}

令N = 100,1000,10000,100000，......

测试函数：

int main()
{int N;scanf("%d", &N);printN(N);return 0;
}

当N大到一定的值时，递归实现的cmd中仅会出现输入的值，而不会输出打印结果。因为递归函数把它能用的空间全部吃掉，还不够吃，所以它就爆掉了，还来不及打印任何数字，就非正常终止了。计算机是不愿意跑递归程序的，因为递归的程序对空间的占用有的时候可能是很恐怖的。（调用其他函数时要先保存当前状态，所以递归程序就在不断的保存当前状态）

这个例子要说明的是：解决问题方法的效率，跟空间的利用效率有关。

1.3：写程序计算给定多项式在给定点x处的值

最直观的做法：

//n表示多项式的阶数，a[]表示每项的系数， x为要求的定点
double f(int n, double a[], double x)
{int i;double p = a[0];for(i = 1; i <=n; i++){p += (a[i] * pow(x, i));}return p;
}

专业程序员是不会这么写的，那专业程序员是怎么处理的呢？

秦九韶巧妙地用了一下结合律：

写程序计算的时候，程序从里往外算，实现的标准程序：

double f(int n, double a[], double x)
{int i;double p = a[n];for (i = n; i > 0; i--){p = a[i-1] + x*p;}return p;
}

为什么第二个程序比第一个程序好呢？因为第一个程序慢得多，怎么测试呢？

C语言中提供了一个函数clock()。

clock()：捕捉从程序开始运行到clock()被调用时所耗费的时间。这个时间单位是clock tick，即“时钟打点”。

常数CLK_TCK：机器时钟每秒所走的时钟打点数。

这两个东西配合在一起，就可以算出一个函数跑了多少秒钟。

计算函数运行时间的模板：

#include <stdio.h>
#include <time.h> //clock()函数在time.h文件中，必须include time.h文件/*clock_t 是clock()函数返回的变量类型*/
clock_t start, stop;
/*记录被测函数运行时间，以秒为单位*/
double duration;int main()
{/*不在测试范围内的准备工作写在clock()调用之前*/start = clock(); /*开始计时*/MyFunction();/*被测函数加在这里*/stop = clock();  /*停止计时*/duration = ((double)(stop - start))/CLK_TCK;/*其他不在测试范围的处理写在后面，例如输入duration的值*/return 0;
}

现在写程序计算给定多项式在给定点x=1.1处的值 $f(1.1)$ .

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "polynomial.h"/*clock_t 是clock()函数返回的变量类型*/
clock_t start, stop;
/*记录被测函数运行时间，以秒为单位*/
double duration;#define MAXN 10 /*多项式最大系数，即多项式阶数+1*/int main()
{int i;double a[MAXN];for(i = 0; i < MAXN; i++) a[i] = (double)i;/*不在测试范围内的准备工作写在clock()调用之前*/start = clock(); /*开始计时*/f1(MAXN-1, a, 1.1);/*被测函数加在这里*/stop = clock();  /*停止计时*/duration = ((double)(stop - start))/CLK_TCK;/*其他不在测试范围的处理写在后面，例如输入duration的值*/printf("ticks1 = %f\n", (double)(stop - start));printf("duration1= %6.2e\n", duration);start = clock(); /*开始计时*/f2(MAXN-1, a, 1.1);/*被测函数加在这里*/stop = clock();  /*停止计时*/duration = ((double)(stop - start))/CLK_TCK;/*其他不在测试范围的处理写在后面，例如输入duration的值*/printf("ticks2 = %f\n", (double)(stop - start));printf("duration2= %6.2e\n", duration);return 0;
}

运行结果：

结果相同，且全为0是因为这两个函数跑得实在太快了，运行时间不到一个tick，所以clock函数根本捕捉不到区别。

那么如何测出不到1tick的程序运行时间？答案：重复！

如果函数跑一次太快，跑得不到一个tick，就让被测函数重复运行充分多次，使得测出的总的时钟打点间隔充分长，最后计算被测函数平均每次运行的时间即可！

所以修改之前的code：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "polynomial.h"clock_t start, stop;double duration;#define MAXN 10 /*多项式最大系数，即多项式阶数+1*/
#define MAXK 1e7 /*被测函数最大重复调用次数*/int main()
{int i;double a[MAXN];for(i = 0; i < MAXN; i++) a[i] = (double)i;start = clock();for (i = 0; i < MAXK; i++) /*重复调用函数以获得充分多的时间间隔*/f1(MAXN-1, a, 1.1);stop = clock();duration = ((double)(stop - start))/CLK_TCK/MAXK;printf("ticks1 = %f\n", (double)(stop - start));printf("duration1= %6.2e\n", duration);start = clock();for (i = 0; i < MAXK; i++) /*重复调用函数以获得充分多的时间间隔*/f2(MAXN-1, a, 1.1);stop = clock();duration = ((double)(stop - start))/CLK_TCK/MAXK;printf("ticks2 = %f\n", (double)(stop - start));printf("duration2= %6.2e\n", duration);return 0;
}

运行结果：

可以看到第一个算法比第二个算法慢了一个数量级。上述程序中仅涉及到了加减乘除，机器做加减法的速度比乘除法快很多，此处的加减法操作可以忽略不计，所以就是具体要看做了多少次乘法。

第一个程序执行的乘法次数为（n²+n）÷2：

double f1(int n, double a[], double x)
{int i;double p = a[0];for(i = 1; i <=n; i++){//pow操作会执行i-1次乘法，前面还有一次乘法操作，所以每次循环会执行i次乘法//所以一共要执行乘法的次数为：1+2+3+......+n = （n²+n）/2次p += (a[i] * pow(x, i)); }return p;
}

第二个程序执行乘法的次数为n：

double f2(int n, double a[], double x)
{int i;double p = a[n];for (i = n; i > 0; i--){p = a[i-1] + x*p; //每次循环执行1次乘法，所以一共执行n次乘法}return p;
}

这个例子要说明的是：解决问题方法的效率，跟算法的巧妙程度有关。

1.4 所以到底什么是数据结构？？？

数据对象在计算机中的组织方式
- 逻辑结构（一对一：线性；一对多：树；多对多：图）
- 物理存储结构（逻辑结构在机器的内存怎么存放的：连续放（数组）还是隔开放（链表））
数据对象必定与一系列加在其上的操作相关联
完成这些操作所用的方法就是算法

抽象数据类型（Abstract Data Type）来描述数据结构。其中涉及到两个概念：

数据类型
- 数据对象集
- 数据结合相关联的操作集
抽象：描述数据类型的方法不依赖于具体实现
- 与存储数据的机器无关
- 与数据存储的物理结构无关
- 与实现操作的算法和编程语言无关

只描述数据对象集合相关操作集“是什么”，并不涉及“如何做到”的问题。

1.5：“矩阵”的抽象数据类型定义

之所以叫做“抽象”，是因为如下几点：

a元素不关心具体类型（float？int？double？）
ElementType：函数返回值的类型不确定
MxN矩阵存储方式不关心：二维数组？一维数组？十字链表？
Add操作具体实现方式不关心：先按行加？先按列加？什么语言？
......

2. 什么是算法

2.1 定义

算法（Algorithm）
- 一个有限指令集
- 接受一些输入（有些情况下不需要输入）
- 产生输出
- 一定在有限步骤之后终止
- 每一条指令必须
  - 有充分明确的目标，不可以有歧义
  - 计算机能处理的范围之内
  - 描述应不依赖于任何一种计算机语言以及具体的实现手段

2.2 什么是好的算法？

衡量算法的指标：

空间复杂度S(n)----------根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限，造成程序非正常中断。
时间复杂度T(n)----------根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。

比如此前的PrintN的递归程序在输入数据规模很大的时候，程序非正常终止，是因为程序在调用其他函数的时候会先保存当前程序的状态（变量等），所以递归程序就会随着输入数据规模的增大而使用更多的内存空间，所以最后爆掉，程序非正常终止。（如下是PrintN(100000）程序空间占用情况

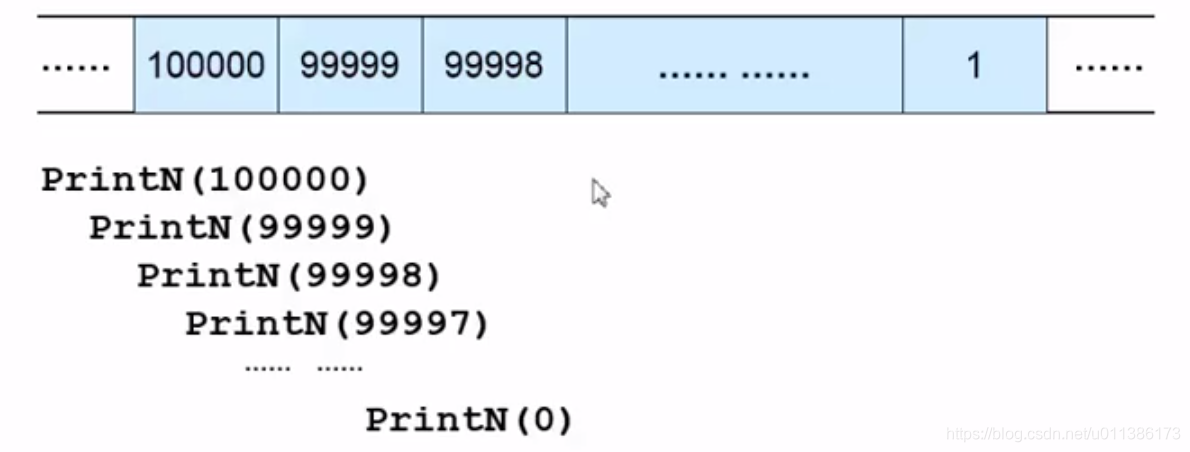
在分析一般算法的效率时，经常关注下面两种复杂度

最坏情况复杂度 $T_{worst}(n)$
平均复杂度 $T_{avg}(n)$

但是平均复杂度比较难搞定，所以我们更关注的是最坏时间复杂度。

2.3 复杂度的渐进表示法

不对算法做精确的分析，只需要知道粗略的增长趋势即可。

$T(n) = O(f(n))$ 表示存在常数 $C> 0,n_{0}> 0$ 使得当 $n\geq n_{0}$ 时有 $T(n)\leq C \cdot f(n)$ --> $f(n)$ 是 $T(n)$ 的某种上界
$T(n)=\Omega (g(n))$ 表示存在常数 $C> 0,n_{0}> 0$ 使得当 $n\geq n_{0}$ 时有 $T(n)\geq C\cdot g(n)$ --> $g(n)$ 是 $T(n)$ 的某种下界
$T(n)=\Theta (h(n))$ 表示同时有 $T(n)=O(h(n))$ 和 $T(n)=\Omega (h(n))$ --> $h(n)$ 既是上界也是下界

下方是一些图表增加一下对不同复杂度的感性理解。

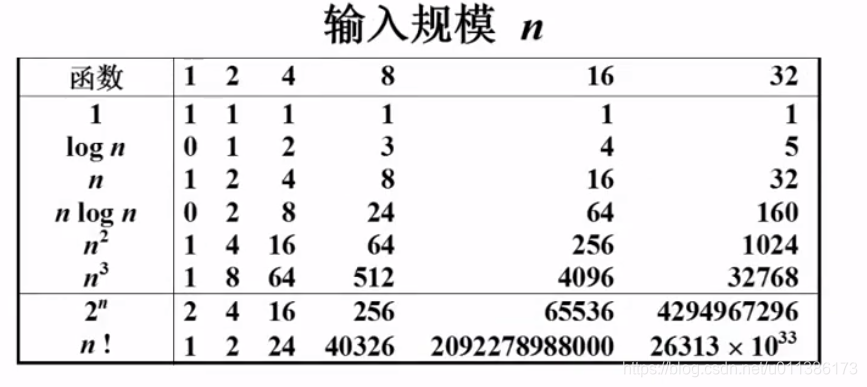
(说明：第一行为规模n，第一列为函数； $log n$ 是以10为底，以2为底还是以e为底其实是不要紧的，不管以什么为底它都只是差了一个常数倍而已）

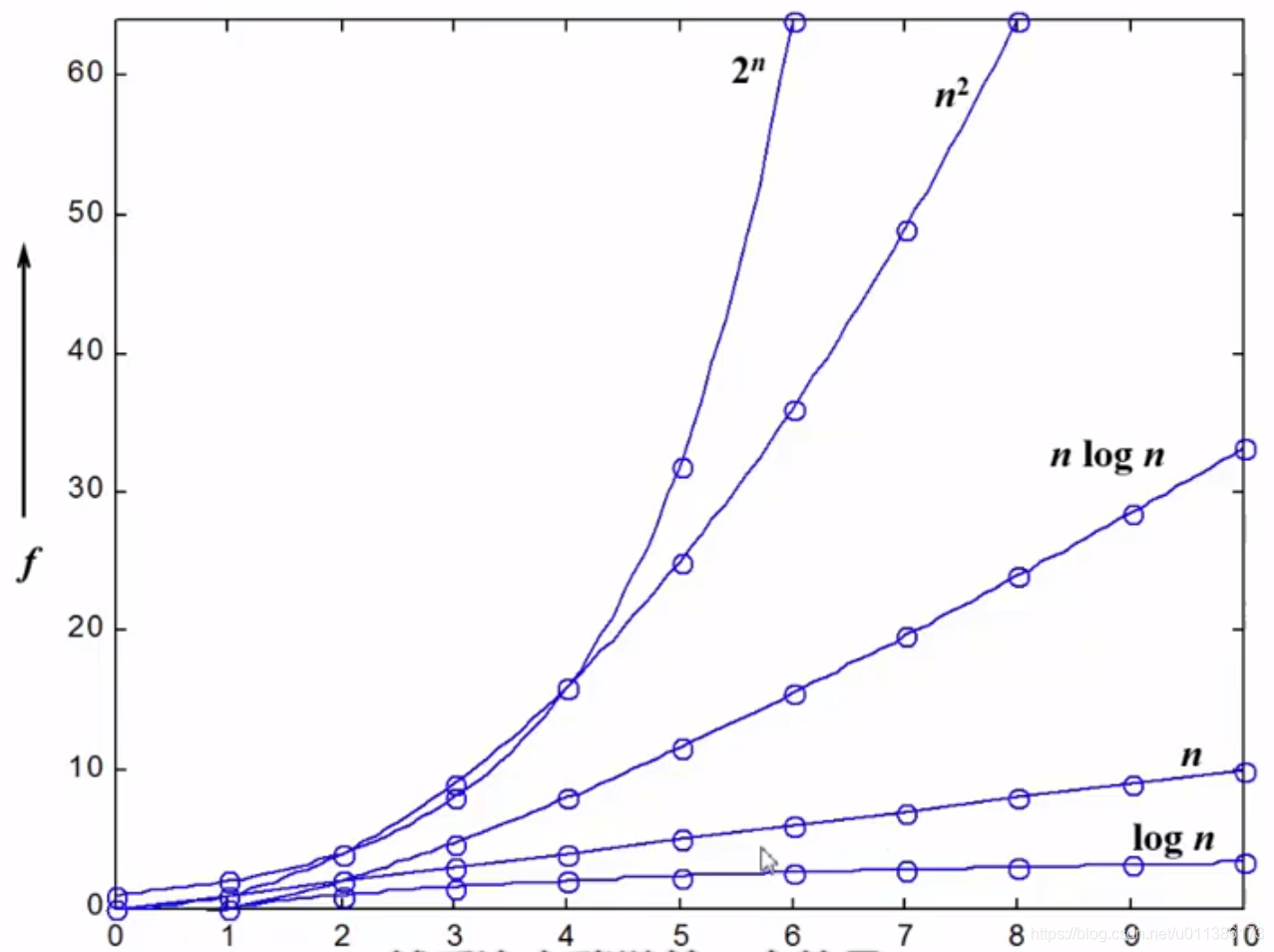
(如果看到某个算法的时间复杂度是 $n^{2}$ ，就要下意识想想能不能把时间复杂度降为 $nlogn$ 。假设规模是一百万，那么 $n^{2}$ 就是一百万乘一百万，而 $nlogn$ 是一百万乘以一个很小的数）

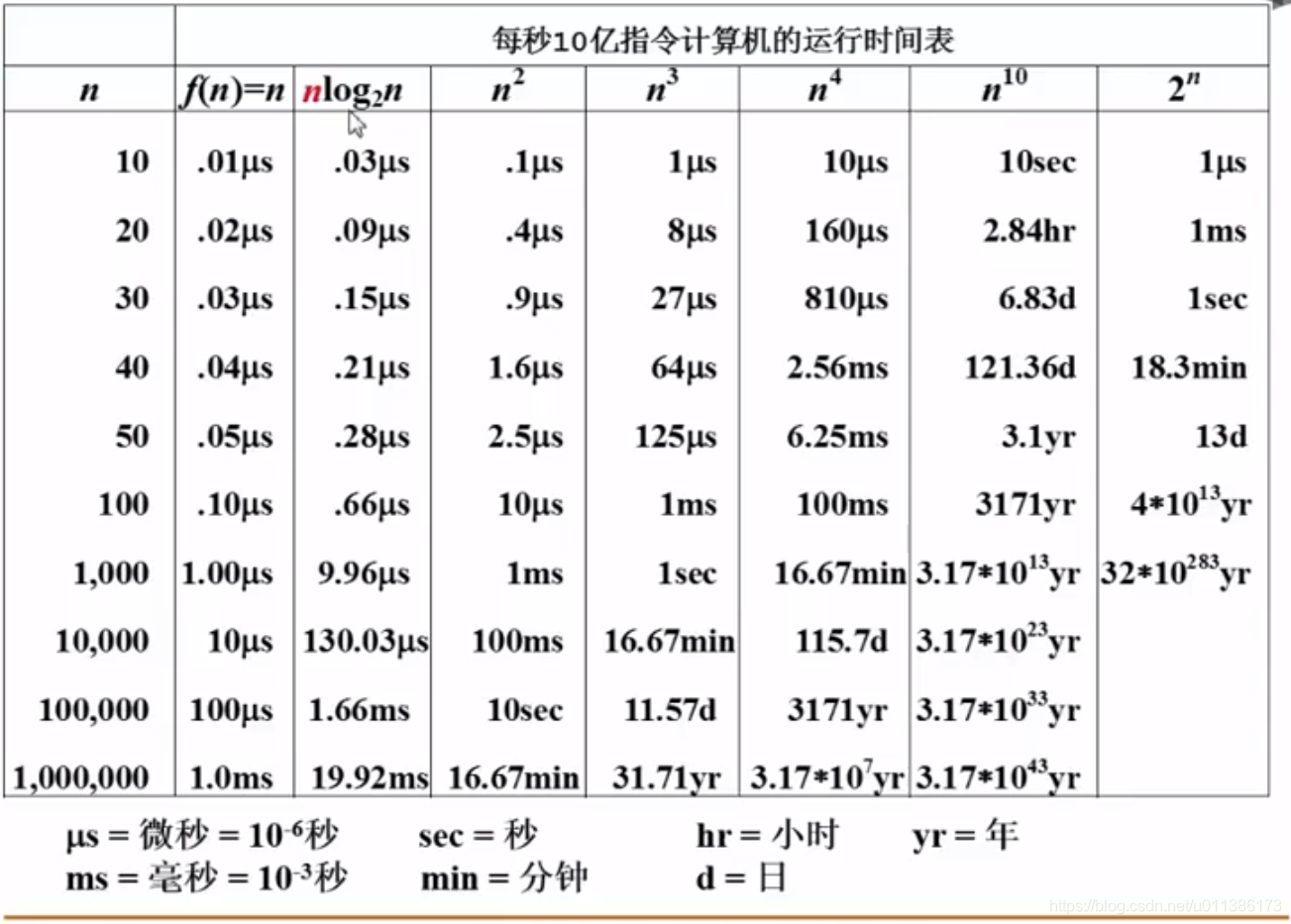
2.4 复杂度分析小窍门

若两段算法分别有复杂度和，则
- $T_{1}(n) + T_{2}(n) = max(O(f_{1}(n)), O(f_{2}(n)))$ -->两段算法拼在一起，总时间就是两段的和，上界就是两个上界中比较大的那个
- $T_{1}(n)\times T_{2}(n) = O(f_{1}(n)\times f_{2}(n))$ -->两段算法嵌套起来时，两个复杂度要相乘的时候，上界为它们上界的乘积
若 $T(n)$ 是关于n的k阶多项式，那么 $T(n)=\Theta(n^{k})$ -->时间复杂度为最高阶
一个for循环的时间复杂度等于循环次数乘以循环体代码的复杂度
if-else结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者中最大

3. 应用实例：最大子列和问题

给定N个整数的序列 $\left \{ {A_{1}, A_{2}, ..., A_{N}} \right \}$ ，求函数的最大值。

3.1 算法1：暴力求解，O(n³）

思路：算出所有连续子列的和，从中找到最大的那个

int MaxSubseqSum1(int A[], int N)
{int ThisSum, MaxSum = 0;int i, j, k;for (i = 0; i < N; i++) /*i是子列左端位置*/{for (j = i; j < N; j++) /*j是子列右端位置*/{ThisSum = 0; /*ThisSum是从A[i]到A[j]的子列和*/for(k = i; k <= j; k++) ThisSum += A[k];if(ThisSum > MaxSum) /*如果刚得到的这个子列和更大*/MaxSum = ThisSum; /*则更新结果*/} /*j循环结束*/}/*i循环结束*/return MaxSum;
}

算法的时间复杂度为 $T(n) = O(N^{3})$ 。

这个方法很笨在于，每次j增大的时候，都要从头开始加，实际上只需要在j-1的基础上再加一个元素就可以了，所以k循环是不需要的。

3.2 算法2 : O(n²）

int MaxSubseqSum2(int A[], int N)
{int ThisSum, MaxSum = 0;int i, j;for (i = 0; i < N; i++) /*i是子列左端位置*/{ThisSum = 0; /*ThisSum是从A[i]到A[j]的子列和*/for (j = i; j < N; j++) /*j是子列右端位置*/{ThisSum += A[j]; /*对于相同的i，不同的j，只要在j-1次循环的基础上累加1项即可*/if (ThisSum > MaxSum) /*如果刚得到的这个子列和更大*/MaxSum = ThisSum; /*则更新结果*/}/*j循环结束*/}/*i循环结束*/return MaxSum;
}

算法的时间复杂度为 $T(n)=O(N^{2})$ 。

相比算法1，已经有很大的改善了。但是如前文我们提到的，当看到算法时间复杂度为 $n^{2}$ 时，应该考虑是否能降为 $nlogn$ ，所以就有了算法3。

3.3 算法3：分而治之， O(nlogn)

大体思路：把一个比较大的问题切分成小的块，然后分头去解决它们，最后再把结果合并起来。

算法思路：

把数组从中间一分为二，然后递归地去解决左右两边的问题（
1. ）递归地解决左边的问题，会得到左边的一个最大子列和；
2. ）递归地解决右边的问题，会得到右边的一个最大子列和；
3. ）跨越边界的最大子列和

找到这三个结果后，那么最后的结果一定是这三个数中间最大的那一个。

切分数组叫做“分”，最后的合成叫做“治”，总起来就叫做“分而治之”。

实例：

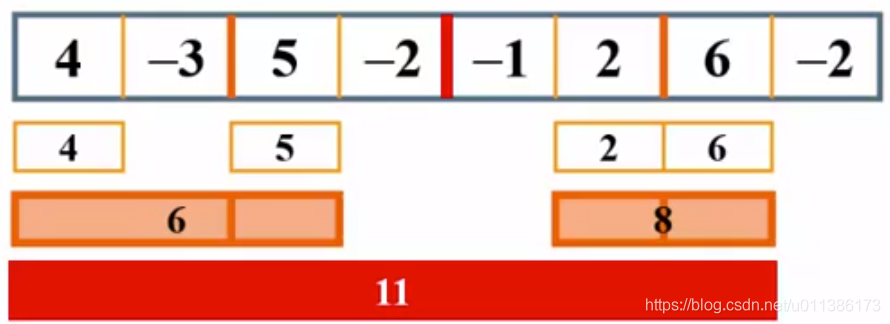
首先，假设数组中有8个元素，如上图所示，我们先沿红色的线从中间分开，得到两部分，发现可以进一步的划分，直到使用黄色的线划分完毕。
首先看4，-3，我们可以看出最大的值为4，这里我们记下最大值为4；然后看5，-2，记下最大值5。同样的道理可以得到最大值2，6。
下一步，我们来看跨越分割线的最大值，首先是4，-3，5，-2这4个数。从-3开始向左，得到最大的值（1）要加到4；然后向右，得到最大的值为5，这样得到跨越边界的最大值为6（即4+(-3)+5）。比较红线左侧得到的最大值4、5、6，得到最大值为6。同理我们可以得到右侧的最大值为8.
同理继续向下，跨越红色的最大值为11（即6 + （-2） + （-1）+ 8），这样得到所有子空间的最大值为11。

算法代码：

int max3Num(int a, int b, int c)
{int maxNum = -1;if (a > b) maxNum = a;else maxNum = b;if (c > maxNum) maxNum = c;return maxNum;
}int divideAndConquer(int List[], int left, int right)
{/*分治法求List[left]到List[right]最大子列和*/int maxLeftSum; //存放左子问题的解int maxLeftBorderSum; //存放左边跨边界的结果int maxRightSum; //存放右子问题的解int maxRightBorderSum; //存放右边跨边界的结果int leftBorderSum; //存放做左子问题跨边界的解int rightBorderSum; //存放右子问题跨边界的解if(left == right) //递归终止条件，子列只有1个数字{if(List[left] > 0) return List[left];else return 0;}int mid = (left + right) / 2;/*递归求得两边子列的最大和*/maxLeftSum = divideAndConquer(List, left, mid);maxRightSum = divideAndConquer(List, mid+1, right);/*求解跨分界线的最大子列和*/maxLeftBorderSum = 0;leftBorderSum = 0;int i;for(i = mid; i >= left; i--) /*从中线向左扫描*/{leftBorderSum += List[i];if (leftBorderSum > maxLeftBorderSum)maxLeftBorderSum = leftBorderSum;} /*左边扫描结束*/maxRightBorderSum = 0;rightBorderSum = 0;int j;for (j = mid+1; j <= right; j++) /*从中线向右扫描*/{rightBorderSum += List[j];if (rightBorderSum > maxRightBorderSum)maxRightBorderSum = rightBorderSum;}/*右边扫描结束*/printf("maxLeftSum=%d, maxRightSum=%d, maxLeftBorderSum=%d,maxRightBorderSum=%d, maxLeftBorderSum + maxRightBorderSum=%d\n",maxLeftSum, maxRightSum, maxLeftBorderSum,maxRightBorderSum,maxLeftBorderSum + maxRightBorderSum);int result = max3Num(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum);printf("The final result = %d\n", result);return result;
}

传入的数组为{4, -3, 5, -2, -1, 2, 6, -2}，打印出的信息：

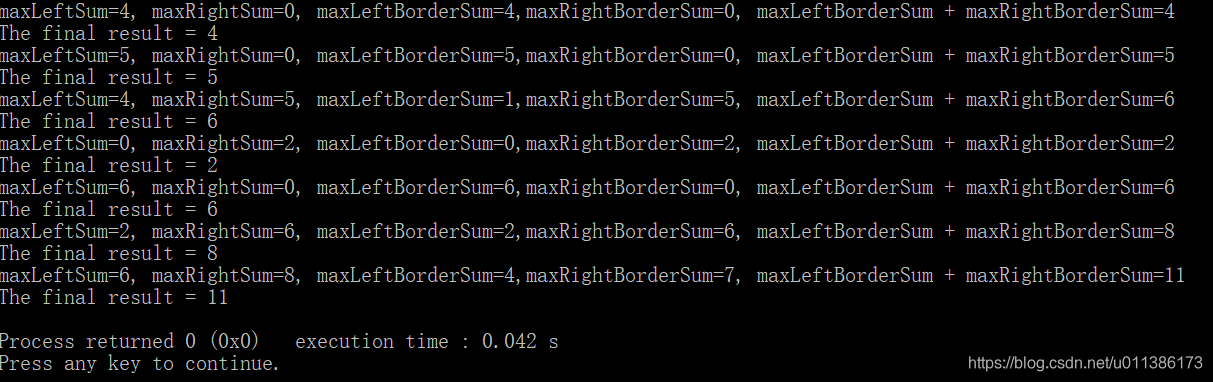
一共7次，恰好可以对应到上面分析的每一步，最终结果为11。

该算法的算法时间复杂度计算过程：假设问题规模为N，从中间一分为二，那么：

左边子问题的规模为 $T(N/2)$ ，
右边子问题的规模也为 $T(N/2)$ ，
而计算跨分界的问题的过程是从中间开始，往左边扫描，然后往右边扫描，每一个元素都被扫描了一次，所以得到该结果的复杂度应是N的常数倍 $O(N)$

因此到的一个 $T(N)$ 的递推公式：

$T(N) = 2T(N/2) + c\cdot N$ , $T(1) = O(1)$

$=2[2T(N/2^{2}) + c \cdot N/2] + c\cdot N$

$=2^{k}O(1) + c\cdot k N$ 其中 $N/2^{k} = 1$ (所以 $2^{^{k}} = N, k = logN$ )

$= O(N) + O(NlogN)$ （两个时间复杂度相加时，取复杂度大的）

$= O(NlogN)$

即是说分而治之算法的时间复杂度为 $O(NlogN)$ 。但是这并不是最快的算法，还有一个更快的算法，叫做“在线处理”算法。

3.4 算法4：在线处理，O(n)

int MaxSubseqSum4(int A[], int N)
{int thisSum, maxSum;int i;thisSum = maxSum = 0;for(i = 0; i < N; i++){thisSum += A[i]; /*向右累加*/if (thisSum > maxSum)maxSum = thisSum; /*发现更大和则更新当前结果*/else if (thisSum < 0) /*如果当前子列和为负*/thisSum = 0;  /*则不可能使后面的部分和增大，抛弃之*/}return maxSum;
}

测试数组：{-1, 3, -2, 4, -6, 1, 6, -1}，运行结果为7。

“在线”的意思是指每输入一个数据就进行即时处理，在任何一个地方终止输入，算法都能正确给出当前的解。

如下是四个算法在某个机器上运行时间比较：

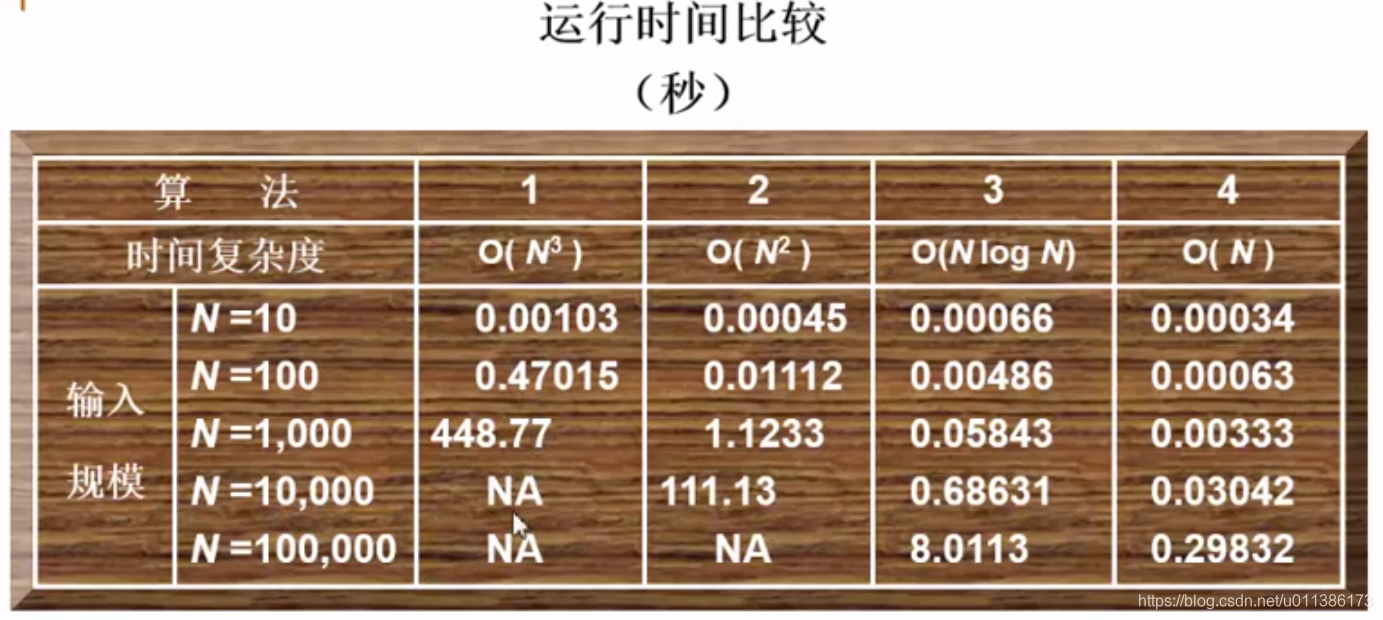
这个时间不包括输入输出的时间。

4. PAT测验

题目1：01-复杂度1 最大子列和问题 (20 分)

01-复杂度1 最大子列和问题 (20 分)

给定K个整数组成的序列{ N1, N2, ..., NK }，“连续子列”被定义为{ Ni, Ni+1, ..., Nj }，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

数据1：与样例等价，测试基本正确性；
数据2：102个随机整数；
数据3：103个随机整数；
数据4：104个随机整数；
数据5：105个随机整数；

输入格式:

输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。

输出格式:

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例:

6
-2 11 -4 13 -5 -2

输出样例:

时间限制: 50000 ms

内存限制: 64 MB

代码长度限制: 16 KB

方法1：(在线处理）

#include <stdio.h>
#include <stdlib.h>
int maxSubseqSum(int a[], int n);int main()
{int n;scanf("%d", &n);int index;int a[n];int positiveCount = 0;for (index = 0; index < n; index++){scanf("%d", &a[index]);if (a[index] < 0)positiveCount++;}int result;if(positiveCount == n)result = 0;elseresult = maxSubseqSum(a, n);printf("%d\n", result);return 0;
}int maxSubseqSum(int a[], int n)
{int i;int currentSum = 0;int maxSum = 0;for (i = 0; i < n; i++){currentSum += a[i];if (currentSum > maxSum)maxSum = currentSum;else if (currentSum < 0)currentSum = 0;}return maxSum;
}

运行结果：

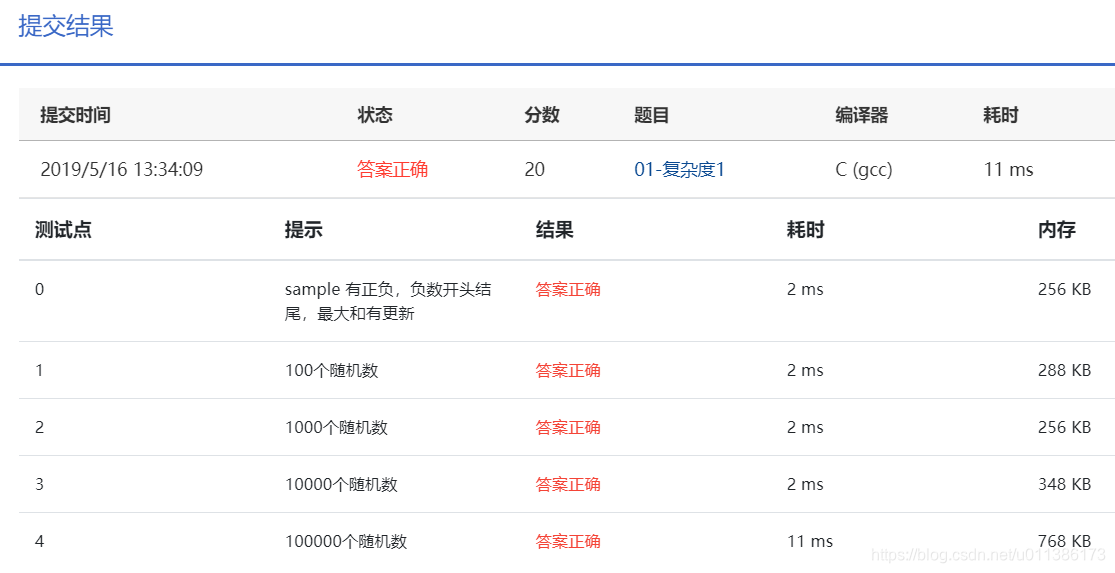
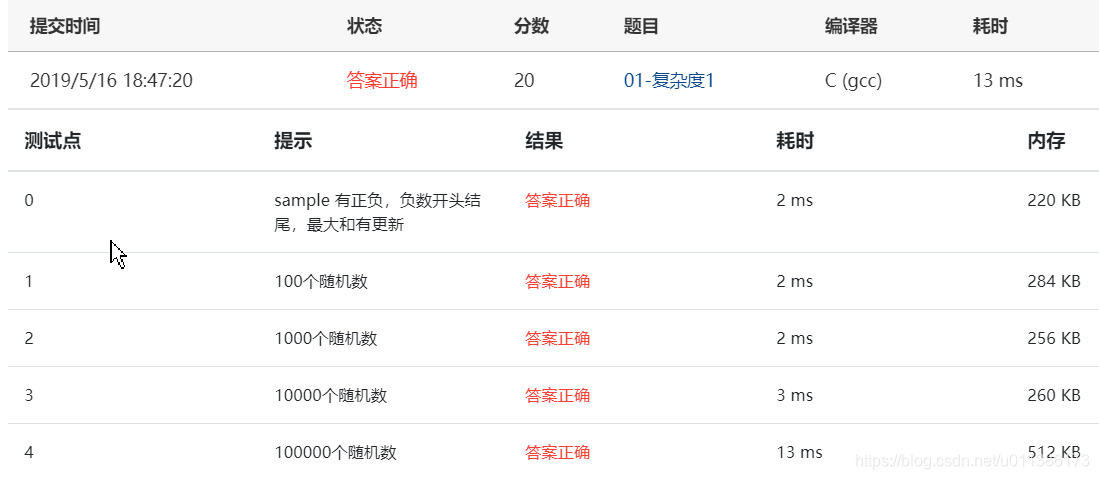
方法2：(分而治之）

#include <stdio.h>int max3Num(int a, int b, int c)
{return a > b ? a > c ? a : c : b > c ? b : c;
}int divideAndConquer(int a[], int left, int right)
{if (left == right){if (a[left] > 0) return a[left];return 0;}int mid = (left + right)/2;int maxLeftSum = divideAndConquer(a, left, mid);int maxRightSum = divideAndConquer(a, mid+1, right);int maxLeftBorderSum = 0;int leftBorderSum = 0;int i;for(i = mid; i >= left; i--){leftBorderSum += a[i];if (leftBorderSum > maxLeftBorderSum)maxLeftBorderSum = leftBorderSum;}int maxRightBorderSum = 0;int rightBorderSum = 0;int j;for (j = mid+1; j <= right; j++){rightBorderSum += a[j];if(rightBorderSum > maxRightBorderSum)maxRightBorderSum = rightBorderSum;}return max3Num(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum);
}int maxSubseqSum2(int a[], int n)
{return divideAndConquer(a, 0, n-1);
}int main()
{int n;if(scanf("%d", &n) != 1) return 0;int index;int a[n];int positiveCount = 0;for (index = 0; index < n; index++){if (scanf("%d", &a[index]) != 1) return 0;if (a[index] < 0)positiveCount++;}int result;if(positiveCount == n)result = 0;elseresult = maxSubseqSum2(a, n);printf("%d\n", result);return 0;
}

运行结果：

另外有个值得注意的地方，当没有判断scanf的返回值时，即仅写为：

scanf("%d", &n);

PAT会提示如下警告信息：

a.c: In function ‘main’:
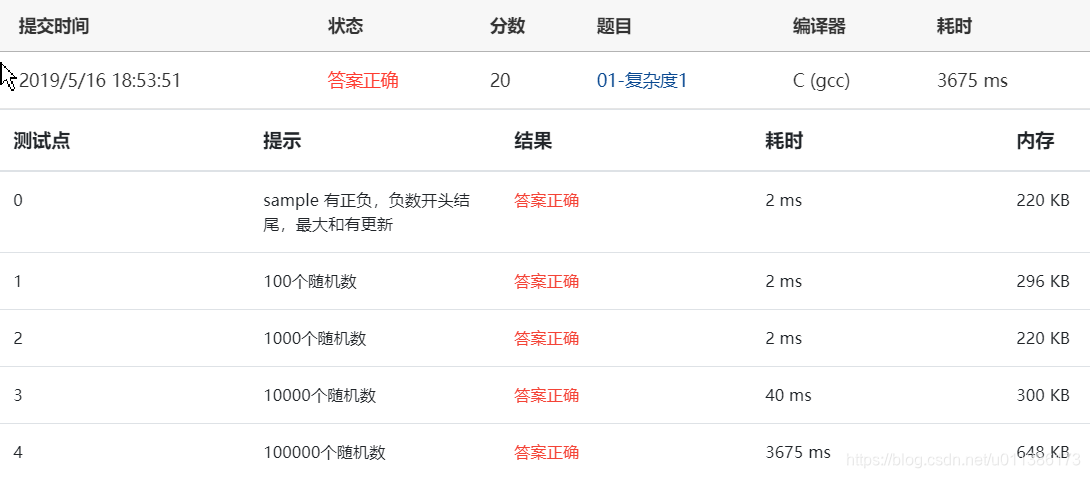
a.c:51:5: warning: ignoring return value of ‘scanf’, declared with attribute warn_unused_result [-Wunused-result]scanf("%d", &n);^~~~~~~~~~~~~~~

方法3：暴力求解O(n²）

#include <stdio.h>int maxSubseqSum3(int a[], int n)
{int i, j;int currentSum = 0;int maxSum = 0;for(i = 0; i < n; i++){currentSum = 0;for(j = i; j < n; j++){currentSum += a[j];if(currentSum > maxSum)maxSum = currentSum;}}return maxSum;
}int main()
{int n;if(scanf("%d", &n) != 1) return 0;int index;int a[n];int positiveCount = 0;for (index = 0; index < n; index++){if (scanf("%d", &a[index]) != 1) return 0;if (a[index] < 0)positiveCount++;}int result;if(positiveCount == n)result = 0;elseresult = maxSubseqSum3(a, n);printf("%d\n", result);return 0;
}

运行结果：

题目2：01-复杂度2 Maximum Subsequence Sum (25 分)

Given a sequence of K integers { N1, N2, ..., NK }. A continuous subsequence is defined to be { Ni, Ni+1, ..., Nj } where 1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.

Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.

Input Specification:

Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.

Output Specification:

For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case意思是子序列不唯一的时候，输出下标较小的一组). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.

Sample Input:

-10 1 2 3 4 -5 -23 3 7 -21

Sample Output:

10 1 4

时间限制: 200 ms

内存限制: 64 MB

代码长度限制: 16 KB

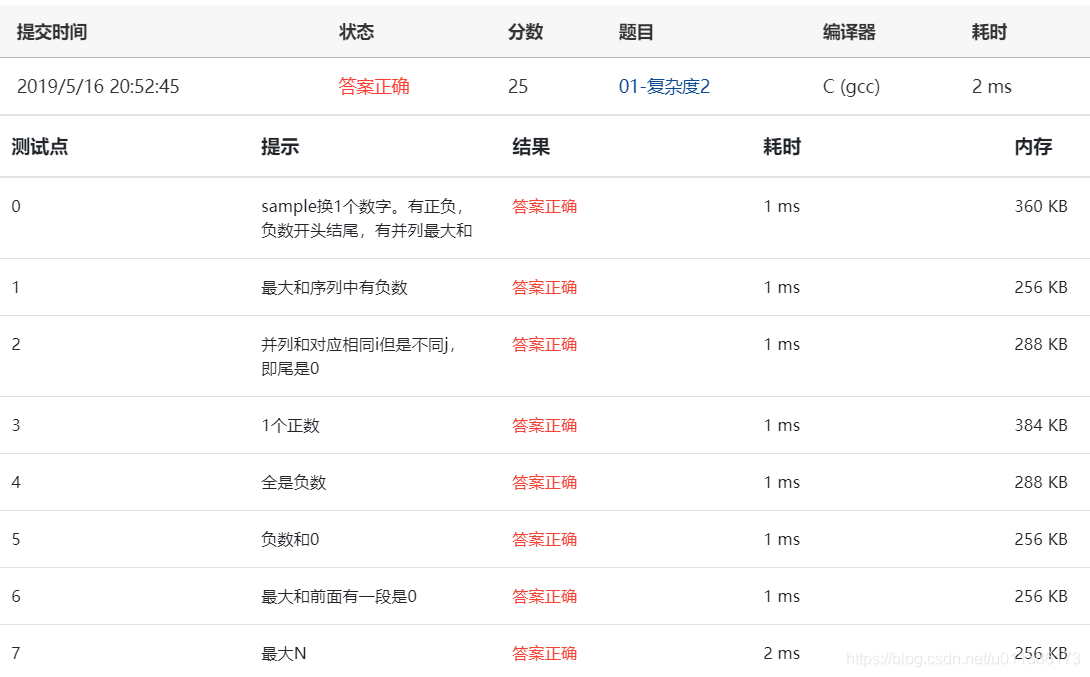
方法1：在线处理

#include <stdio.h>void maxSubseqSum(int a[], int n)
{int i;int curSum = 0;int maxSum = 0;int startPos = 0;int endPos = 0;int tmpStartPos = 0;for(i = 0; i < n; i++){curSum += a[i];if(curSum > maxSum || curSum == maxSum && maxSum ==0) //包含了数组为负数和0的情况{maxSum = curSum;startPos = tmpStartPos;endPos = i;}else if (curSum < 0){curSum = 0;tmpStartPos = i+1;}}printf("%d %d %d\n", maxSum, a[startPos], a[endPos]);
}int main()
{int n;if(scanf("%d", &n) != 1) return 0;int index;int a[n];int isAllNegative = 1;for (index = 0; index < n; index++){if (scanf("%d", &a[index]) != 1) return 0;if (a[index] >= 0)isAllNegative = 0;}if(isAllNegative)printf("0 %d %d", a[0], a[n-1]);elsemaxSubseqSum(a,n);return 0;
}

运行结果：

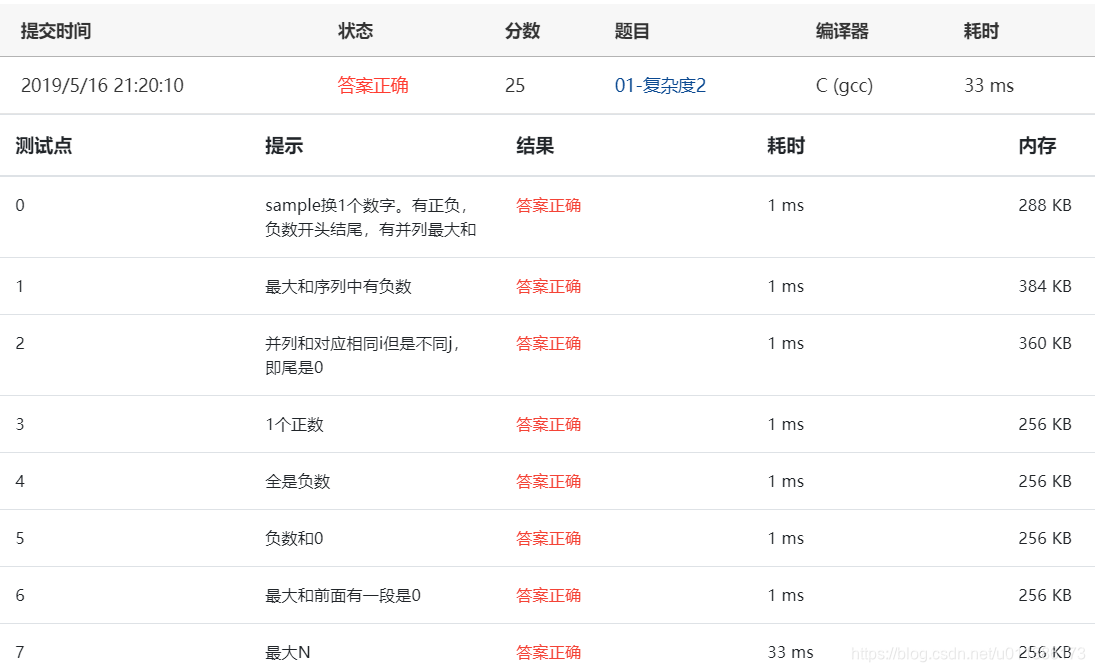
方法2：暴力求解O(n²)

#include <stdio.h>void maxSubseqSumWithNum(int a[], int n)
{int i, j;int currentSum = 0;int maxSum = 0;int startPos = n-1;int endPos = n-1;for(i = n-1; i >=0; i--){currentSum = 0;for(j = i; j >=0; j--){currentSum += a[j];if(currentSum >= maxSum){maxSum = currentSum;endPos = i;startPos = j;}}}printf("%d %d %d", maxSum, a[startPos], a[endPos]);//return maxSum;
}int main()
{int n;if(scanf("%d", &n) != 1) return 0;int index;int a[n];int isAllNegative = 1;for (index = 0; index < n; index++){if (scanf("%d", &a[index]) != 1) return 0;if (a[index] >= 0)isAllNegative = 0;}if(isAllNegative)printf("0 %d %d", a[0], a[n-1]);elsemaxSubseqSumWithNum(a,n);return 0;
}

运行结果：

题目3：01-复杂度3 二分查找 (20 分)

题目描述

本题要求实现二分查找算法。

时间限制: 100 ms内存限制: 64 MB代码长度限制: 16 KB

函数接口定义：

Position BinarySearch( List L, ElementType X );

其中List结构定义如下：

typedef int Position;
typedef struct LNode *List;
struct LNode {ElementType Data[MAXSIZE];Position Last; /* 保存线性表中最后一个元素的位置 */
};

L是用户传入的一个线性表，其中ElementType元素可以通过>、==、<进行比较，并且题目保证传入的数据是递增有序的。函数BinarySearch要查找X在Data中的位置，即数组下标（注意：元素从下标1开始存储）。找到则返回下标，否则返回一个特殊的失败标记NotFound。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 10
#define NotFound 0
typedef int ElementType;typedef int Position;
typedef struct LNode *List;
struct LNode {ElementType Data[MAXSIZE];Position Last; /* 保存线性表中最后一个元素的位置 */
};List ReadInput(); /* 裁判实现，细节不表。元素从下标1开始存储 */
Position BinarySearch( List L, ElementType X );int main()
{List L;ElementType X;Position P;L = ReadInput();scanf("%d", &X);P = BinarySearch( L, X );printf("%d\n", P);return 0;
}/* 你的代码将被嵌在这里 */

输入样例1：

5
12 31 55 89 101
31

输出样例1：

输入样例2：

3
26 78 233
31

输出样例2：

代码：

Position BinarySearch( List L, ElementType X )
{Position low = 1;Position high = L->Last;Position mid = 0;while(low <= high){if(X == L->Data[low])return low;if(X == L->Data[high])return high;/*使用(low+high)/2会有整数溢出的问题（问题会出现在当low+high的结果大于表达式结果类型所能表示的最大值时，这样，产生溢出后再/2是不会产生正确结果的，而low+((high-low)/2)不存在这个问题 */mid =low + (high - low)/2; if (X > L->Data[mid]) //继续在R[mid+1..high]中查找low = mid + 1;else if (X < L->Data[mid])high = mid - 1; //继续在R[low..mid-1]中查找elsereturn mid; //查找成功返回}return NotFound; //当所查找区间内没有结果，查找失败
}

运行结果