【基础算法】(03) 十二种排序算法（第三篇）

本文主要是介绍【基础算法】(03) 十二种排序算法（第三篇），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【基础算法】(03) 十二种排序算法（第三篇）

Auther: Thomas Shen
E-mail: Thomas.shen3904@qq.com
Date: 2017/10/21
All Copyrights reserved !

---

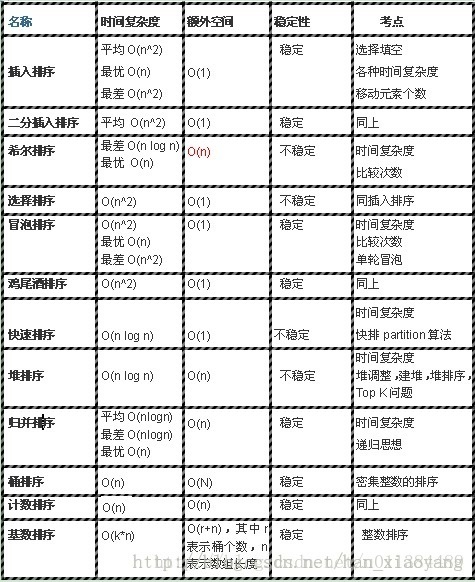
1. 篇述：

本系列总结了常用的十二种排序算法，每个算法都包括算法原理, 代码实现, 面试例题 三部分。

其中本文是排序算法系列的第三篇，介绍了：

• 9. 交换排序—快速排序（Quick Sort）,
• 10. 归并排序（Merge Sort）,

---

2. 直接插入排序 (Straight Insertion Sort)：

3. 二分插入排序 （Binary insert sort)：

4. 希尔排序 （Shell’s Sort）：

5. 选择排序—简单选择排序（Simple Selection Sort）：

6. 选择排序—堆排序（Heap Sort）：

7. 交换排序—冒泡排序（Bubble Sort）：

8. 鸡尾酒排序/双向冒泡排序：

参见第一、二篇；

---

9. 交换排序—快速排序（Quick Sort）：

快速排序基本思想是通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

9.1 原理简介：

快速排序使用分治法来把一个串（list）分为两个子串行（sub-lists）。

步骤为：

1. 从数列中挑出一个元素，称为 “基准”（pivot）;
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n^2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

最差时间复杂度 O(n^2)
最优时间复杂度 O(n log n)
平均时间复杂度 O(n log n)
最差空间复杂度 : 根据实现的方式不同而不同

快速排序是通常被认为在同数量级（O(nlog2n)）的排序方法中平均性能最好的。但若初始序列按关键码有序或基本有序时，快排序反而蜕化为冒泡排序。

为改进之，通常以“三者取中法”来选取基准记录，即将排序区间的两个端点与中点三个记录关键码居中的调整为支点记录。快速排序是一个不稳定的排序方法。

9.2 代码实现：

9.2.1 版本一：
我们选取数组的第一个元素作为主元，每一轮都是和第一个元素比较大小，通过交换，分成大于和小于它的前后两部分，再递归处理。

/************************************************** 函数功能：对数组快速排序                        函数参数：指向整型数组arr的首指针arr；           整型变量left和right左右边界的下标    函数返回值：空                                   
/**************************************************/  
void QuickSort(int *arr, int left, int right)  
{  int i,j;  if(left<right){  i=left;j=right;  //准备以本次最左边的元素值为标准进行划分，先保存其值arr[0]=arr[i];   do {  while(arr[j]>arr[0] && i<j)   j--;  //从右向左找第1个小于标准值的位置j  if(i<j) {   //找到了，位置为jarr[i] = arr[j];  i++;  }           //将第j个元素置于左端并重置i  while(arr[i]<arr[0] && i<j)  i++;      //从左向右找第1个大于标准值的位置i  if(i<j){//找到了，位置为iarr[j] = arr[i];  j--;  }//将第i个元素置于右端并重置j  }while(i!=j);  //将标准值放入它的最终位置,本次划分结束 arr[i] = arr[0]; //对标准值左半部递归调用本函数quicksort(arr, left, i-1); //对标准值右半部递归调用本函数   quicksort(arr, i+1, right);  }  
}  

9.2.2 版本二：
随机选基准数的快排 :

//使用引用，完成两数交换  
void Swap(int& a , int& b)  
{  int temp = a; a = b; b = temp;  
} //取区间内随机数的函数  
int Rand(int low, int high)  
{  int size = hgh - low + 1;  return  low + rand()%size;   
} //快排的partition算法，这里的基准数是随机选取的  
int RandPartition(int* data, int low , int high)  
{      swap(data[rand(low,high)], data[low]);int key = data[low];  int i = low;  for(int j=low+1; j<=high; j++)  {  if(data[j]<=key)  {  i = i+1;  swap(data[i], data[j]);  }              }   swap(data[i],data[low]);  return i;  
}//递归完成快速排序  
void QuickSort(int* data, int low, int high)  
{  if(low<high)  {  int k = RandPartition(data,low,high);  QuickSort(data,low,k-1);  QuickSort(data,k+1,high);  }  
}  

9.3 快速排序的改进：
在本改进算法中,只对长度大于k的子序列递归调用快速排序,让原序列基本有序，然后再对整个基本有序序列用插入排序算法排序。实践证明，改进后的算法时间复杂度有所降低，且当k取值为 8 左右时,改进算法的性能最佳。算法思想如下：

void print(int a[], int n){  for(int j= 0; j<n; j++){  cout<<a[j] <<"  ";  }  cout<<endl;  
}  void swap(int *a, int *b)  
{  int tmp = *a;  *a = *b;  *b = tmp;  
}  int partition(int a[], int low, int high)  
{  int privotKey = a[low];                 //基准元素  while(low < high){                   //从表的两端交替地向中间扫描  while(low < high  && a[high] >= privotKey) --high; //从high 所指位置向前搜索，至多到low+1 位置。将比基准元素小的交换到低端  swap(&a[low], &a[high]);  while(low < high  && a[low] <= privotKey ) ++low;  swap(&a[low], &a[high]);  }  print(a,10);  return low;  
}  void qsort_improve(int r[ ],int low,int high, int k){  if( high -low > k ) { //长度大于k时递归, k为指定的数  int pivot = partition(r, low, high); // 调用的Partition算法保持不变  qsort_improve(r, low, pivot - 1,k);  qsort_improve(r, pivot + 1, high,k);  }   
}   
void quickSort(int r[], int n, int k){  qsort_improve(r,0,n,k);//先调用改进算法Qsort使之基本有序  //再用插入排序对基本有序序列排序  for(int i=1; i<=n;i ++){  int tmp = r[i];   int j=i-1;  while(tmp < r[j]){  r[j+1]=r[j]; j=j-1;   }  r[j+1] = tmp;  }   
}int main(){  int a[10] = {3,1,5,7,2,4,9,6,10,8};  cout<<"初始值：";  print(a,10);  quickSort(a,9,4);  cout<<"结果：";  print(a,10);  }  

9.4 面试例题：
9.4.1 例题1：
最小的k个数，输入n个整数，找出其中最下的k个数，例如输入4、5、1、6、2、7、3、8、1、2，输出最下的4个数，则输出1、1、2、2。

当然，博主也知道这题可以建大小为k的大顶堆，然后用堆的方法解决。
但是这个题目可也以仿照快速排序，运用partition函数进行求解，不过我们完整的快速排序分割后要递归地对前后两段继续进行分割，而这里我们需要做的是判定分割的位置，然后再确定对前段还是后段进行分割，所以只对单侧分割即可。

代码如下：

void GetLeastNumbers_by_partition(int* input, int n, int* output, int k)  
{  if(input == NULL || output == NULL || k > n || n <= 0 || k <= 0)  return;  int start = 0;  int end = n - 1;  int index = Partition(input, n, start, end);  while(index != k - 1)  {  if(index > k - 1)  {  end = index - 1;  index = Partition(input, n, start, end);  }  else  {  start = index + 1;  index = Partition(input, n, start, end);  }  }  for(int i = 0; i < k; ++i)  output[i] = input[i];  
}  

9.4.2 例题2：
判断数组中出现超过一半的数字。

当然，这道题很多人都见过，而且最通用的一种解法是数对对消的思路。这里只是再给大家提供一种思路，快排partition的方法在很多地方都能使用，比如这题。我们也可以选择合适的判定条件进行递归。

代码如下：

bool g_bInputInvalid = false;  
bool CheckInvalidArray(int* numbers, int length)  
{  g_bInputInvalid = false;  if(numbers == NULL && length <= 0)  g_bInputInvalid = true;  return g_bInputInvalid;  
}  
bool CheckMoreThanHalf(int* numbers, int length, int number)  
{  int times = 0;  for(int i = 0; i < length; ++i)  {  if(numbers[i] == number)  times++;  }  bool isMoreThanHalf = true;  if(times * 2 <= length)  {  g_bInputInvalid = true;  isMoreThanHalf = false;  }  return isMoreThanHalf;  
}  
int MoreThanHalfNum_Solution1(int* numbers, int length)  
{  if(CheckInvalidArray(numbers, length))  return 0;  int middle = length >> 1;  int start = 0;  int end = length - 1;  int index = Partition(numbers, length, start, end);  while(index != middle)  {  if(index > middle)  {  end = index - 1;  index = Partition(numbers, length, start, end);  }  else  {  start = index + 1;  index = Partition(numbers, length, start, end);  }  }  int result = numbers[middle];  if(!CheckMoreThanHalf(numbers, length, result))  result = 0;  return result;  
}  

9.4.3 例题3：
有一个由大小写组成的字符串，现在需要对他进行修改，将其中的所有小写字母排在大写字母的前面(不要求保持原顺序)。

这题可能大家都能想到的方法是：设置首尾两个指针，首指针向后移动寻找大写字母，尾指针向前移动需找小写字母，找到后都停下，交换。之后继续移动，直至相遇。这种方法在这里我就不做讨论写代码了。

代码如下：

#include <iostream>  
using namespace std;  
void Proc( char *str )  
{  int i = 0;  int j = 0;  //移动指针i, 使其指向第一个大写字母  while( str[i] != '\0' && str[i] >= 'a' && str[i] <= 'z' )       i++;  if( str[i] != '\0' )  {  //指针j遍历未处理的部分，找到第一个小写字母  for( j=i; str[j] != '\0'; j++ )  {  if( str[j] >= 'a' && str[j] <= 'z' )  {  char tmp = str[i];  str[i] = str[j];  str[j] = tmp;  i++;  }  }  }  
}  
int main()  
{  char data[] = "SONGjianGoodBest";  Proc( data );  return 0;  
}  

---

10. 归并排序（Merge Sort）：

10.1 原理简介：

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

归并排序具体算法描述如下(递归版本)：

1. Divide: 把长度为n的输入序列分成两个长度为n/2的子序列。
2. Conquer: 对这两个子序列分别采用归并排序。
3. Combine: 将两个排序好的子序列合并成一个最终的排序序列。

归并排序的效率是比较高的，设数列长为N，将数列分开成小数列一共要logN步，每步都是一个合并有序数列的过程，时间复杂度可以记为O(N)，故一共为O(N*logN)。因为归并排序每次都是在相邻的数据中进行操作，所以归并排序在O(N*logN)的几种排序方法（快速排序，归并排序，希尔排序，堆排序）也是效率比较高的。

10.2 代码实现：

//将有二个有序数列a[first...mid]和a[mid...last]合并。  
void MergeArray(int a[], int first, int mid, int last, int temp[])  
{  int i = first, j = mid + 1;  int m = mid,   n = last;  int k = 0;  while (i <= m && j <= n)  {  if (a[i] <= a[j])  temp[k++] = a[i++];  else  temp[k++] = a[j++];  }  while (i <= m)  temp[k++] = a[i++];  while (j <= n)  temp[k++] = a[j++];  for (i = 0; i < k; i++)  a[first + i] = temp[i];  
}

//递归地完成归并排序  
void MergeSort(int a[], int first, int last, int temp[])  
{  if (first < last)  {  int mid = (first + last) / 2;  mergesort(a, first, mid, temp);    //左边有序  mergesort(a, mid + 1, last, temp); //右边有序  mergearray(a, first, mid, last, temp); //再将二个有序数列合并  }  
}  

10.3 面试例题：
10.3.1 例题一：
输入一个数组，数组元素的大小在0->999.999.999的范围内，元素个数为0-500000范围。题目要求通过相邻的元素的交换，使得输入的数组变为有序，要求输出交换的次数。

这题求解的其实就是一个逆序对。我们回想一下归并排序的过程：
归并排序是用分治思想，分治模式在每一层递归上有三个步骤：

• 分解：将n个元素分成个含n/2个元素的子序列。
• 解决：用合并排序法对两个子序列递归的排序。
• 合并：合并两个已排序的子序列已得到排序结果。

在归并排序算法中稍作修改，就可以在n log n的时间内求逆序对。

将数组A[1…size]，划分为A[1…mid] 和 A[mid+1…size].那么逆序对数的个数为 f(1, size) = f(1, mid) + f(mid+1, size) + s(1, mid, size)，这里s(1, mid, size)代表左值在[1—mid]中，右值在[mid+1, size]中的逆序对数。由于两个子序列本身都已经排序，所以查找起来非常方便。

代码如下：

#include<iostream>  
#include<stdlib.h>  
using namespace std;  
void printArray(int arry[],int len)  
{  for(int i=0;i<len;i++)  cout<<arry[i]<<" ";  cout<<endl;  
}  
int MergeArray(int arry[],int start,int mid,int end,int temp[])//数组的归并操作  
{  //int leftLen=mid-start+1;//arry[start...mid]左半段长度  //int rightLlen=end-mid;//arry[mid+1...end]右半段长度  int i=mid;  int j=end;  int k=0;//临时数组末尾坐标  int count=0;  //设定两个指针ij分别指向两段有序数组的头元素，将小的那一个放入到临时数组中去。  while(i>=start&&j>mid)  {  if(arry[i]>arry[j])  {  temp[k++]=arry[i--];//从临时数组的最后一个位置开始排序  count+=j-mid;//因为arry[mid+1...j...end]是有序的，如果arry[i]>arry[j]，那么也大于arry[j]之前的元素，从a[mid+1...j]一共有j-(mid+1)+1=j-mid  }  else  {  temp[k++]=arry[j--];  }  }  cout<<"调用MergeArray时的count："<<count<<endl;  while(i>=start)//表示前半段数组中还有元素未放入临时数组  {  temp[k++]=arry[i--];  }  while(j>mid)  {  temp[k++]=arry[j--];  }  //将临时数组中的元素写回到原数组当中去。  for(i=0;i<k;i++)  arry[end-i]=temp[i];  printArray(arry,8);//输出进过一次归并以后的数组，用于理解整体过程  return count;  
}  
int InversePairsCore(int arry[],int start,int end,int temp[])  
{  int inversions = 0;    if(start<end)  {  int mid=(start+end)/2;  inversions+=InversePairsCore(arry,start,mid,temp);//找左半段的逆序对数目inversions+=InversePairsCore(arry,mid+1,end,temp);//找右半段的逆序对数目inversions+=MergeArray(arry,start,mid,end,temp);//在找完左右半段逆序对以后两段数组有序，然后找两段之间的逆序对。最小的逆序段只有一个元素。  }      return inversions;  
}  
int InversePairs(int arry[],int len)  
{  int *temp=new int[len];  int count=InversePairsCore(arry,0,len-1,temp);  delete[] temp;  return count;  
}  
void main()  
{  //int arry[]={7,5,6,4};  int arry[]={1,3,7,8,2,4,6,5};  int len=sizeof(arry)/sizeof(int);  //printArray(arry,len);  int count=InversePairs(arry,len);  //printArray(arry,len);  //cout<<count<<endl;  system("pause");  
} 

10.3.2 例题二：
归并一个左右两边分别排好序的数组，空间复杂度要求O(1)。

使用原地归并，能够让归并排序的空间复杂度降为O(1)，但是速度上会有一定程度的下降。

代码如下：

#include<iostream>  
#include<cmath>  
#include<cstdlib>  
#include<Windows.h>  
using namespace std;  
void insert_sort(int arr[],int n)  
{  for(int i=1;i<n;++i)  {  int val=arr[i];  int j=i-1;  while(arr[j]>val&&j>=0)  {  arr[j+1]=arr[j];  --j;  }  arr[j+1]=val;  }  
}  void aux_merge(int arr[],int n,int m,int aux[])  
{  for(int i=0;i<m;++i)  swap(aux[i],arr[n+i]);  int p=n-1,q=m-1;  int dst=n+m-1;  for(int i=0;i<n+m;++i)  {  if(p>=0)  {  if(q>=0)  {  if(arr[p]>aux[q])  {  swap(arr[p],arr[dst]);  p--;  }  else  {  swap(aux[q],arr[dst]);  q--;  }  }  else  break;  }  else  {  swap(aux[q],arr[dst]);  q--;  }  dst--;  }  
}  
void local_merge(int arr[],int n)  
{  int m=sqrt((float)n);  int k=n/m;  for(int i=0;i<m;++i)  swap(arr[k*m-m+i],arr[n/2/m*m+i]);  for(int i=0;i<k-2;++i)  {  int index=i;  for(int j=i+1;j<k-1;++j)  if(arr[j*m]<arr[index*m])  index=j;  if(index!=i)  for(int j=0;j<m;++j)  swap(arr[i*m+j],arr[index*m+j]);  }  for(int i=0;i<k-2;++i)  aux_merge(arr+i*m,m,m,arr+(k-1)*m);  int s=n%m+m;  insert_sort(arr+(n-2*s),2*s);  aux_merge(arr,n-2*s,s,arr+(k-1)*m);  insert_sort(arr+(k-1)*m,s);  }  
void local_merge_sort(int arr[],int n)  
{  if(n<=1)  return;  if(n<=10)  {  insert_sort(arr,n);  return;  }  local_merge_sort(arr,n/2);  local_merge_sort(arr+n/2,n-n/2);  local_merge(arr,n);  
}  
void merge_sort(int arr[],int temp[],int n)  
{  if(n<=1)  return;  if(n<=10)  {  insert_sort(arr,n);  return;  }  merge_sort(arr,temp,n/2);  merge_sort(arr+n/2,temp,n-n/2);  for(int i=0;i<n/2;++i)  temp[i]=arr[i];  for(int i=n/2;i<n;++i)  temp[n+n/2-i-1]=arr[i];  int left=0,right=n-1;  for(int i=0;i<n;++i)  if(temp[left]<temp[right])  arr[i]=temp[left++];  else  arr[i]=temp[right--];  
}  const int n=2000000;  
int arr1[n],arr2[n];  
int temp[n];  int main()  
{  for(int i=0;i<n;++i)  arr1[i]=arr2[i]=rand();  int begin=GetTickCount();  merge_sort(arr1,temp,n);  cout<<GetTickCount()-begin<<endl;  begin=GetTickCount();  local_merge_sort(arr2,n);  cout<<GetTickCount()-begin<<endl;  for(int i=0;i<n;++i)  if(arr1[i]!=arr2[i])  cout<<"ERROR"<<endl;  system("pause");  
}  

---

11. 桶排序 (Bucket sort)：

12. 计数排序 (Counting sort)：

13. 基数排序 (Radix Sort)：

参见第四篇；

---

14. 总结：

---

References. ：

• [ 1 ]. Coursera | Java程序设计 | PKU
• [ 2 ]. 转载自：八大排序算法
• [ 3 ]. 转载自：12种排序算法详解

这篇关于【基础算法】(03) 十二种排序算法（第三篇）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---