本文主要是介绍【Angew】:催化材料中贵金属的最大效率-原子分散表面铂,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

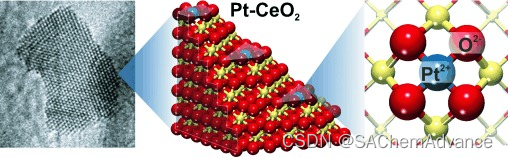
图形摘要:通过在纳米结构 CeO2的 {100}“纳米袋”中稳定表面 Pt2+物种(见图) ,可以制备具有最高贵金属分散度的Pt-CeO2材料。此类材料可以大大减少催化剂所需的贵金属量。
摘要:贵金属Pt是催化领域用途最广泛的元素,但它非常稀有,而且价格昂贵,限制了其大规模应用,例如在燃料电池技术中的应用。然而,传统催化剂仅使用 Pt 含量的一小部分,即位于催化剂表面的原子。为了最大限度地提高贵金属效率,贵金属应以原子形式分散,并仅位于材料的最外层表面层内。这种原子分散的 Pt 表面物种确实可以制备得具有极高的稳定性。使用 DFT 计算,我们确定了一种特定的结构元素,即二氧化铈“纳米袋”,它与 Pt2+的结合非常牢固,以至于可以承受烧结和本体扩散。在模型催化剂上,我们通过实验证实了理论预测的稳定性,并且在燃料电池催化中表现出高 Pt 效率的真实 Pt-CeO2纳米复合材料上,我们还确定了这些锚定位点。
减少对 Pt(和其他铂族金属,PGM)的需求的目标是催化研究的主要驱动力。有两种策略可以应对这一挑战:第一种是用新的、更便宜、更丰富的材料替代珍贵的贵金属。此策略被提出但到目前为止,许多不含贵金属的催化剂无法与昂贵的同类催化剂竞争。自从贵金属被用于非均相催化以来,人们一直遵循第二种简单直接的策略:其理念是尽可能高效地使用昂贵的金属。在这种情况下,最关键的参数是分散度,即暴露于反应物的金属原子的比例。负载在高表面积氧化物上的小PGM 纳米颗粒(NP)通常用于催化材料以实现高分散度。然而,在大多数反应中,真正活跃的仍然只是金属的一小部分。
我们应该如何设计一种“理想的催化材料”,以最大限度地利用贵金属成分?在这种理想的材料中,每一个单独的贵金属原子都应该能被反应物接触。换句话说,整个贵金属含量应该以原子的形式分散在催化材料的表面层。实际上,最近发现原子分散的铂(和金)微量存在于氧化铈上时具有催化活性。这类系统代表了一类新的催化剂——原子分散的负载金属催化剂。
然而,仅仅制备原子分散催化剂是不够的。在许多催化反应的苛刻条件下,两种现象常常导致催化剂的快速失活:颗粒的烧结和活性金属的体相扩散会减少表面原子的比例。因此,“理想的催化材料”还必须能够稳定活性金属原子,防止其发生聚集和体相扩散。换句话说,我们需要将原子分散的活性原子牢固地锚定在表面,使其能够抵抗聚集成纳米颗粒和向更深层扩散的趋势。
在此,研究者将理论与实验相结合,确定了一种满足这两个要求的原子分散 Pt 催化剂的目标结构。通过密度泛函理论 (DFT) 计算,我们确定了一种具有独特性质的结构元素:位于 CeO2纳米面方平面配位位点的表面 Pt2+离子。理论预测这种结构单元应该非常稳定,能够抵抗聚集成金属 Pt NP。此外,它只能在表面形成,从而防止 Pt 扩散到体内。通过超高真空 (UHV) 下的模型催化实验,我们表明这些 Pt2+中心确实存在于表面,并且确实具有预测的稳定性。在通过薄膜技术制备的真实二氧化铈纳米颗粒上,我们识别出相同的 Pt2+物质,并找到这些原子分散物质稳定的 {100} 纳米面。
在图1中,我们总结了DFT研究的结果。我们通过分析合适的氧化铈纳米颗粒,开始寻找“理想”的铂位点。最近,我们已经展示了氧化铈纳米结构对其表面特性的关键控制作用。我们确定了立方八面体Ce40O80纳米颗粒作为纳米结构氧化铈的代表模型(图1)。该纳米颗粒呈现出截断八面体的形状,具有氧终止的{111}和非常小的{100}纳米晶面。{100}纳米晶面对应于极性(100)表面,其稳定性显著低于氧化铈的(111)表面。然而,这些{100}纳米晶面在纳米结构氧化铈中是丰富的结构元素。正如我们将要展示的,它们在本研究中发挥了关键作用。
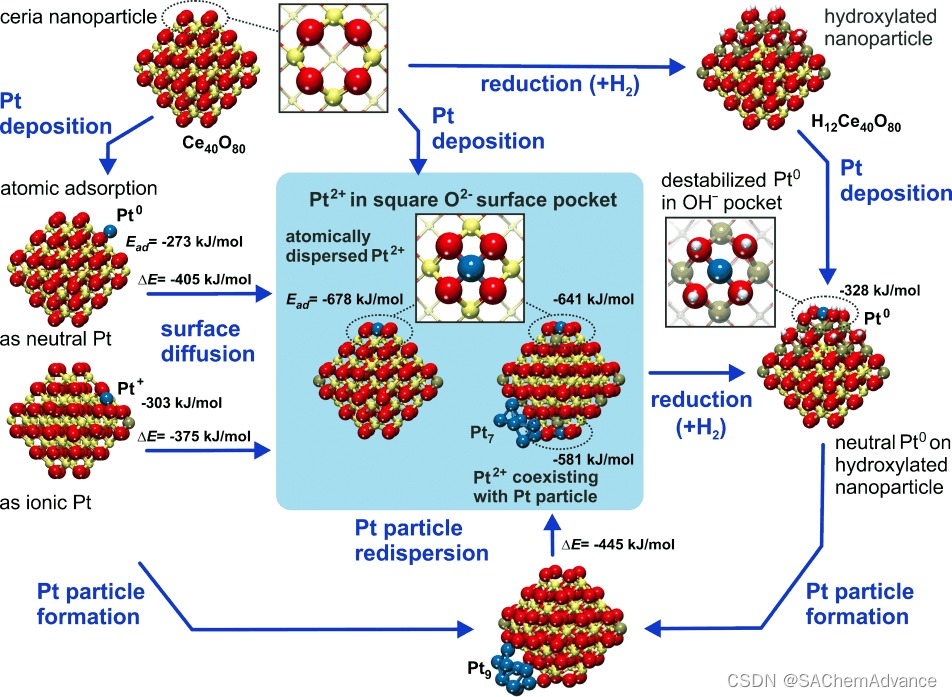
将原子 Pt 放置在 Ce40O80NP 的各个位置。我们发现{111} 面上存在中等强度的结合(吸附能为 −273 至 −303 kJ mol−1 ),分别产生 Pt0和 Pt+状态(有关详细信息,请参阅附件)。吸附能与在常规 CeO2 (111) 表面上计算出的吸附能相似(−256 kJ mol−1)。Pt的形式电荷态由吸附时还原的 Ce 阳离子数量决定,即Ce4+(4f0)→Ce3+ (4f1 )。
令人惊讶的是,吸附在{100}纳米晶面上的原子铂表现得完全不同。通过捐赠两个电子获得了2+状态,从而形成了两个Ce3+中心(图1)。最重要的是,吸附能非常大:Pt2+与氧化物的结合能高达678 kJ/mol。金属原子与氧化物表面的这种强烈相互作用表明形成了表面配位化合物,其中支撑物充当多齿配体。显然,具有四个O2−离子的“表面口袋”(最近邻距离为315–320 pm,见SI中的图S1a)提供了一个理想的“基质”来容纳Pt2+(d8)离子。实际上,我们的计算揭示了一个几乎平面四边形结构的形成,其中中央原子Pt2+仅比表面氧阴离子的平面高出11 pm。与Pt原子结合后,O2−正方形收缩到最近邻距离为289-290 pm,导致Pt–O距离为205 pm(图S1b)。这种收缩需要显著的结构柔性,而纳米颗粒很容易提供这种柔性。请注意,O终止的{100}晶面并不是纳米颗粒上唯一可以容纳平面四边形配位的Pt2+离子的位置。通过将纳米颗粒的一个角Ce原子替换为Pt原子并释放一个O原子,也会形成相同的局部PtO4结构(特征为Pt2+,图S1d)。我们注意到,在先前对实际催化剂的EXAFS(扩展X射线吸收精细结构)研究中,曾推测原子铂可能确实位于氧离子的平面四边形排列中。我们的DFT计算确定了这些位点的原子结构,并揭示了它们惊人的稳定性。
由于Pt2+离子在{100}“纳米孔隙”中的强锚定,产生了显著的后果。这些后果在图1中总结了。锚定的Pt2+离子的吸附能超过了块状Pt的内聚能(-564 kJ mol-1)。这有一个重要的结果:锚定的Pt2+在热力学上是稳定的,不会发生烧结,即不会形成金属Pt纳米粒子。因此,我们预计锚定的Pt2+能够承受高温退火。实际上,甚至有可能O2-纳米孔隙能够从支持的Pt颗粒中抽取Pt原子。我们通过DFT计算证明了这一路径的放热性(图1和图S2)。例如,在Ce40O80上的Pt9颗粒中,抽取两个Pt原子在能量上是有利的:该反应生成了位于{100}纳米面的两个Pt2+离子和四个新的Ce3+中心,并留下一个Pt7聚集体。然而,是否能够在实际中观察到这种重新分散过程,将取决于活化能和所应用的实验条件。
要理解固定的Pt2+可能的形成过程,有两个其他方面尤为重要。首先,我们必须问,分散的金属是否会作为Pt纳米粒子的成核点。如果是这样,Pt2+将很容易被共存的金属Pt覆盖。为了回答这个问题,我们研究了Pt2二聚体的形成,在常规CeO2(111)上,该过程是强烈放热的(369 kJ/mol)。相反,固定的Pt2+并不倾向于与另一个Pt原子形成键。没有发现对应于Pt–Pt2+/O4基团的局部最小值,在几何优化过程中,二聚体解离成Pt2+/O4复合物和吸附在附近的中性Pt原子。这一发现表明,固定的Pt2+物种实际上可以与金属Pt纳米粒子共存,而不会被多余的Pt掩埋。值得注意的是,CO与固定的Pt2+离子的相互作用非常弱(7 kJ/mol),这表明Pt2+几乎不受CO吸附的干扰。
第二个重要方面是氧化或还原氧化铈会如何影响锚定的Pt2+离子的稳定性。我们研究了Pt在Ce40O80的{100}纳米晶面上逐步还原的过程中吸附的情况,通过H原子的吸附(图1和图S3)。当多达八个O原子在Pt2+/O4复合物附近被氢化时(Pt/Ce40O72(OH)8),锚定的Pt2+的吸附能仅略微下降(约为-600 kJ/mol,见图S3)。然而,进一步的氢化(在Pt2+/O4基团附近氢化12个O原子,Pt/Ce40O68(OH)12)将Pt原子的吸附能降低到低于金属内聚能的水平;换句话说,锚定的Pt2+离子在热力学上变得不稳定,会形成Pt纳米颗粒。正如预期的那样,如此强烈的还原作用也导致Pt2+被还原为Pt0(图1、图S1c和图S3)。结果,两个Pt-O键被打破,平面四方结构丧失,吸附能降至-328 kJ/mol,这样的结合强度太弱,无法阻止Pt的聚集。确实,氧化的Pt在氧化铈上高度分散,在流动的H2中加热至600°C时会聚集。我们的模型现在提供了这种现象的微观图像,并阐明了其能量学。
概述的理论模型预测,在纳米结构的CeO2表面可以制备出非常稳定的原子分散的Pt2+物种。此外,我们目前的计算结果表明,O4纳米孔穴也能稳定许多其他金属防止聚集,例如Pd、Ni、Co和Cu。因此,这种类型的金属-载体相互作用似乎普遍促进了单金属原子催化剂的形成。
阳离子物种在高温下形成并停留在表面,能够抵抗烧结和扩散到主体。这一预测可以通过模型催化实验进行验证。在模型催化中,我们在“理想”条件下制备定义明确的表面,即从原子级清洁的单晶表面开始,在超高真空(UHV)条件下进行。这一策略允许逐步构建复杂表面,同时在任何阶段,这些模型都可以通过表面科学的光谱和显微方法进行研究。
研究者从一个有序且完全化学计量的 CeO2(111) 薄膜开始构建我们的模型系统,该薄膜在 Cu(111) 上制备(实验细节见SI)。在这种表面上蒸汽沉积活性金属是制备负载模型催化剂的标准方法。然而,在这种表面上沉积 Pt(如同其他贵金属)通常会导致大尺寸纳米颗粒的成核和生长。考虑到我们的 DFT 数据,这并不令人惊讶,因为理想且有序的 CeO2(111) 表面并不提供 {100} 纳米晶面来捕获金属离子。因此,他们探索了一种新的制备方法:在氧气氛中同时共沉积 Ce 和 Pt(实验细节见SI)。在所应用的条件下,已知 Ce 会形成 CeO2 纳米颗粒。我们预计,在这些颗粒生长过程中,Pt 应该会被掺入并以 Pt2+的形式被困在它们的 {100} 纳米晶面上。扫描隧道显微镜(STM)研究表明,这些表面显示出直径约为 3 nm、典型高度约为 0.4 nm 的三维岛的生长(图 2a)。确实,一些聚集体显示出具有晶面形状的迹象,这并不令人意外,表明 CeO2 纳米颗粒在 CeO2(111) 载体上具有外延生长。图 2b 显示了这些纳米颗粒的示意图。尽管主要由 {111} 晶面终止,但也可能暴露出小的 {100} 纳米晶面,从而可以容纳原子分散的 Pt2+。
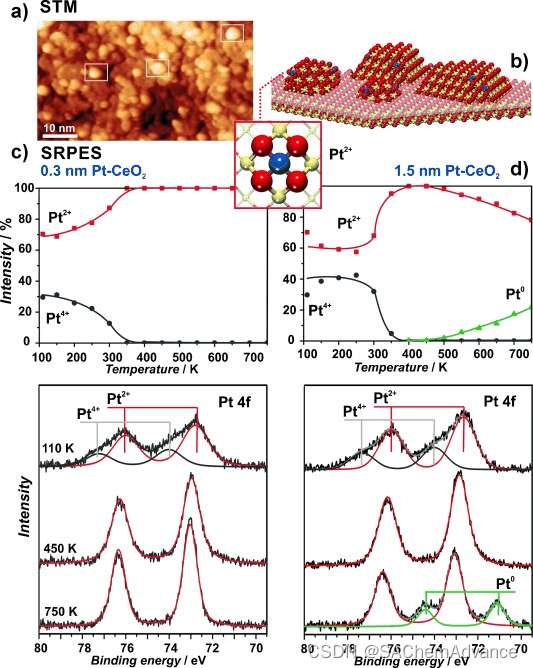
为了探究是否确实如此,我们进行了同步辐射光电子能谱(SRPES)实验(图2c)。事实上,在低温(110K)下沉积后,我们检测不到金属Pt,而仅检测到氧化态为+2和+4的离子Pt。加热时,Pt4+的信号迅速减弱,表明Pt4+离子相当不稳定(与DFT计算结果一致,见图S1d)。然而,Pt2+物种的表现符合理论预测。它们表现出卓越的热稳定性,甚至在我们模型表面可测试的最高温度(约750K)下仍保持稳定。注意,随着加热,Pt2+的信号甚至增加。鉴于光电子的平均自由程约为0.5nm(最大表面敏感度下拍摄的光谱),这一增加表明Pt2+物种并没有通过体扩散损失,而是迁移到了CeO2纳米颗粒的表面。通过图2d所示的第二次实验结果,证明了提供适当表面位点以锚定Pt的关键作用。在这种情况下,我们在相同条件下共同沉积了几层CeO2和Pt单分子层。加热后,Pt2+部分还原并烧结成金属纳米颗粒。显然,多层膜不能提供足够数量的表面{100}纳米口袋来锚定所有沉积的Pt。那些位于体内或不利晶面的原子由于结合力太弱,无法抵抗烧结成金属纳米颗粒的趋势。
虽然超高真空模型实验令人印象深刻地展示了表面锚定的Pt2+物种的稳定性,但这些实验无法制备足够大规模的材料以用于实际应用。然而,另一种薄膜沉积技术,即磁控溅射,可以实现这一点。尽管磁控溅射在催化剂制备中是一种相对非常规的技术,但它具有可扩展性,并且在技术过程中经常使用。最近,我们展示了通过磁控溅射可以制备高孔隙率涂层,这意味着它在催化领域具有很高的应用潜力。更有趣的是,通过共溅射,可以制备具有任意Pt:Ce比例的分散Pt-CeO2复合材料,直接类似于上面讨论的模型催化剂。我们还证明了Pt-CeO2涂层作为质子交换膜燃料电池技术中的电催化剂具有优越的贵金属效率。最近,我们比较了不同Pt负载量(0到10 μg Pt/cm²)的Pt-CeO2阳极(见SI)。性能最高的是含有2 μg Pt/cm²的催化剂,其中仅包含Pt2+离子。对于更高的负载量,Pt既存在于Pt2+状态也存在于Pt0状态,催化剂的性能较低(SI,图S5)。尽管详细的反应机制尚未确定,但我们的研究清楚地表明,当仅存在离子态铂时,Pt-CeO2电催化剂表现出非凡的活性。
在此,我们通过共溅射到石墨箔上制备 Pt-CeO2纳米材料,并通过 SRPES 和高分辨率透射电子显微镜 (HRTEM,图 3 ) 对这些材料进行表征。事实上,SRPES 显示 Pt 的氧化态为 +2 和 +4,与模型催化剂一样。请注意,光谱再次在低光子能量 (180 eV) 下采集,即具有高表面灵敏度。与体敏感的硬 X 射线光电子能谱 (HAXPES) 相比,确实表明 Pt2+物种优先位于表面。
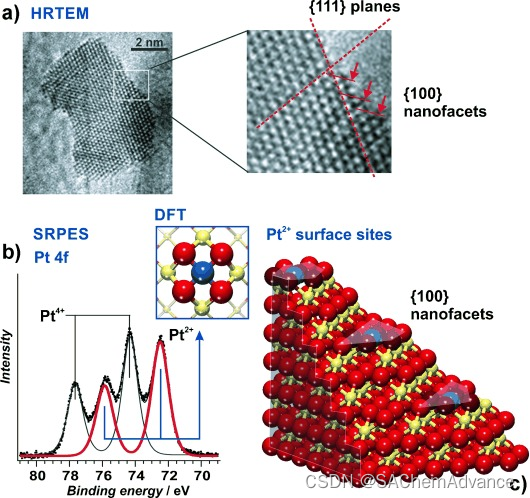
我们能否定位这些材料上锚定Pt2+物种的{100}纳米面?图3a显示了一个从4% Pt-CeO2催化剂表面截取的纳米颗粒的高分辨率透射电子显微镜(HRTEM)图像。该图像对应一个Pt-CeO2颗粒,其特征是交叉的{111}和{100} CeO2晶面。显然,该颗粒被大量小的{100}台阶装饰。图3c展示了这些面的结构模型及其排列。这些{100}纳米面具有锚定Pt2+中心所需的方形O4纳米孔。锚定的Pt2+的高吸附能可能作为额外的驱动力,在生长过程中稳定{100}纳米面,从而有助于Pt-CeO2纳米颗粒上这些有利结构元素的高密度。
总之,我们解决了如何最大限度地高效利用铂,这种在催化中最为多功能且最有价值的贵金属的问题。策略很简单:在我们理想的材料中,贵金属必须原子级分散并仅位于最外层表面。在这种材料的催化反应中,每一个铂原子都能被反应物接触到。挑战在于设计一种能够在反应条件下稳定原子级分散表面铂物种的支撑材料。通过DFT建模,我们确定了纳米结构的氧化铈上的一个结构元素,它有潜力构建这种材料。该结构元素是位于CeO2的{100}纳米晶面一个O2−离子方形孔中的Pt2+离子。理论预测这种结构单元中分散铂的吸附能足够大,可以抵抗热引起的聚集形成金属纳米颗粒以及铂向氧化铈体相的扩散损失。一旦制备好,这种表面锚定的Pt2+在即使是严苛条件下也应保持稳定。在精心控制的表面科学实验中,我们制备了具有表面锚定Pt2+的纳米结构氧化铈模型系统。在这个模型上,我们展示了Pt2+确实位于表面,并在高温下仍然完美稳定,没有还原、烧结或体相扩散现象。为了使这一结果更接近应用,我们通过磁控溅射制备了具有原子级分散铂的CeO2纳米材料。Pt-CeO2纳米材料显示出与模型实验中非常相似的离子态Pt2+表面物种。通过高分辨率电子显微镜,我们在这些材料上识别出大量承载锚定Pt2+物种的CeO2{100}纳米晶面。我们正在进行的基于这些Pt-CeO2纳米材料作为阳极催化剂的燃料电池测试显示,当铂仅以2+态存在时,表现出非常高的性能。
研究表明,原子级别的见解如何帮助在知识驱动的基础上设计贵金属高效材料。例如,原子分散的Pt-CeO2材料可能在减少未来应用中对关键材料的需求方面发挥关键作用。
这篇关于【Angew】:催化材料中贵金属的最大效率-原子分散表面铂的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!