本文主要是介绍回归现实:无需复杂假设即可轻松评估过程能力的简单方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Cpk 和 Ppk 等过程能力指标能够测量您的过程相对于客户规格要求的执行情况。我们先回顾一些能力分析基础知识,再深入了解另一个能力估计值 Cnpk,该估计值很可能在您的能力分析库中非常有用。
能力统计指标分析
能力统计指标使用单个数字,是一种无单位指标,用于评估过程能否满足指定要求以及确定需要改进的领域。为此,可以将此常用估计值视为“客户之声”与“过程之声”的比值。
我们可以轻松测量“客户之声”,即可接受公差或规格限制之间的距离。测量“过程之声”有点棘手,通常会假设测量值来自形状类似于钟形曲线的总体。它有一个方便的属性,大约是 6 个标准差宽,因此“过程之声”大约是标准差的 6 倍。
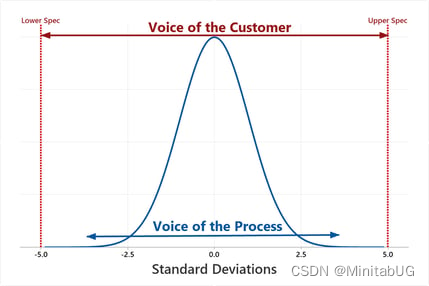
如果公差和过程分布长度相同,则“客户之声”与“过程之声”的比值大约等于 1.0。然而,理想情况下,为了确保尽可能减少缺陷,我们在规格与过程所达处之间有一个小缓冲区。因此,对于缺陷极少的过程,公差必须大于过程分布宽度,使它们的比值大于 1。事实上,Cpk 和 Ppk 等可接受能力统计指标的常见基准值为 1.33 和 1.67。
能力统计指标在实践中的应用
遗憾的是,实际情况通常比本教材中的示例更复杂。比如,有时只有一个规格限制,通常分布不集中在规格限制之间,导致可能需要以多种方式测量标准差。有关这些重要问题的更多信息,请参阅此讨论。此外,我们在考虑现实世界中的数据时,可能会发现,在很多情况下,数据不遵循正态分布曲线(钟形曲线)。
在能力分析情况下,数据分布形状是我们衡量过程分布方式的关键组成部分。如果数据明显偏离假设分布,则 Cpk 和 Ppk 等指标无法准确反映过程能力。庆幸的是,Minitab Statistical Software 包含一套稳健的非正态能力分析工具,能够帮助您处理这种恼人的非正态数据问题。
但是,如果已经尝试通过试错法处理正态分布不拟合问题,该怎么办? 换言之,当统计 > 质量工具 > 个体分布标识中的 Anderson-Darling p 值都低于 0.05 基准值时(表明提供的分布或变换都不合适),我们该怎么办?
当替代分布/变换不足时

我最近在与一家制造静脉输液医疗器械专用管的公司合作时就遇到了这种情况。该公司需要向美国食品药品监督管理局证明,他们的管达到了规定的抗拉强度要求。
下面是我从 Minitab Statistical Software 的“个体分布标识”中获得的结果。
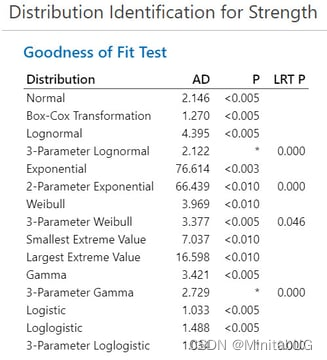
使用 Anderson-Darling 拟合优度检验时,若 p 值高于 0.05,通常表示在评估能力时,可以使用相应的分布或变换。但在该示例中,没有一种方法符合该标准。
我们来仔细研究一下这些数据,看看问题出在哪里。通过图形生成器(图形 > 图形生成器),可以在下方直方图中看到,其中一根样本管的抗拉强度低于要求,另一根管的强度高于要求。异常值是导致分布或变换在此类情况下无效的最常见原因。根据定义,极端异常值不符合数据的一般模式。
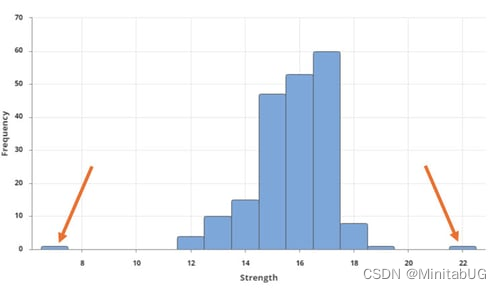
研究极端异常值并尝试了解引起极端异常值的原因非常重要。异常值可能是测量错误或数据输入错误,在这种情况下,它们并不能反映真实过程,应进行适当调整。如果它们是合理值,则首要任务应该是防止未来出现异常值并努力确保过程稳定,但可能仍需要进行能力估计,然后才能将产品投入市场。
用于评估能力的无分布解决方案
Minitab Statistical Software 22 版中最好的一个新功能是非参数能力分析。此分析功能可合理估计过程能力,而无需对分布进行更复杂的假设。要访问此实用功能,选择统计 > 质量工具 > 能力分析 > 非参数。

对于医疗管数据,可以看到,即使在有两个异常值的混乱情况下,过程仍然能够满足规格下限要求。可以像解读 Cpk 和 Ppk 等其他能力统计指标一样来解读非参数能力统计指标 Cnpk。在本例中,Cnpk = 1.39,超出了公司的能力目标 1.33。
分布假设对于能力分析至关重要,因为它们支持基于分析结果的计算、解释、推断和决策。然而,还需要了解的是,真实世界数据可能并不总是完全遵守这种假设。若在工具包中添加一种简单的无分布方法,即使真实世界数据不遵循任何已知分布模式,也能进行适当的能力估计。
这篇关于回归现实:无需复杂假设即可轻松评估过程能力的简单方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






