一文看懂如何增强LLM的长文本处理能力（包含代码和原理解析）

本文主要是介绍一文看懂如何增强LLM的长文本处理能力（包含代码和原理解析），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本篇博客是LLM中的RoPE位置编码代码解析与RoPE的性质分析（一）的续集，若对RoPE的性质不了解（比如远程衰减性、周期性与频率特性），建议先看LLM中的RoPE位置编码代码解析与RoPE的性质分析（一）

如何增强使用RoPE的LLM的处理长文本的能力

我们继续定义模型的训练长度为$L_{train}$，模型的测试长度为$L_{test}$，$L_{test}>L_{train}$，定义$s=\frac{L_{test}}{L_{train}}$为内插因子。

回忆一下RoPE的实现：
$$\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ..\\ q_{d-2}\\ q_{d-1}\end{array}\right]\ast \left[\begin{array}{c}cosm{\theta }_0\\ cosm{\theta }_0\\ cosm{\theta }_1\\ cosm{\theta }_1\\ ..\\ cosm{\theta }_{d/2-1}\\ cosm{\theta }_{d/2-1}\end{array}\right]+\left[\begin{array}{c}-q_1\\ q_0\\ -q_3\\ q_2\\ ..\\ -q_{d-1}\\ q_{d-2}\end{array}\right]\ast \left[\begin{array}{c}sinm{\theta }_0\\ sinm{\theta }_0\\ sinm{\theta }_1\\ sinm{\theta }_1\\ ..\\ sinm{\theta }_{d/2-1}\\ sinm{\theta }_{d/2-1}\end{array}\right](1)$$
在公式(1)中，$m$表示query向量的位置，同时cos函数与sin函数的输入均是$m{\theta }_i$，$i$表示分量。

在RoPE中，$m{\theta }_i$的定义是：
$$f(m,{\theta }_i)=m{\theta }_i=\frac{m}{bas{e}^{2i/d}}(2)$$

对于某个模型来说，$d$是固定的。

位置编码内插是早期对基于RoPE的LLM进行长文本能力扩展的方法。

PI（位置编码内插，Position Interpolation）

EXTENDING CONTEXT WINDOW OF LARGE LANGUAGE MODELS VIA POSITION INTERPOLATION

位置编码内插是指，将超过$L_{train}$的文本的position_id缩放到$[0,L_{train}-1]$。下图的第二行展示了位置编码内插后的效果，可以看到PI之后，原本两个点直接的距离变得更短了，压缩了局部token之间的分辨率，从而可能会造成局部失真。所以PI的方法需要一定量的额外训练，从而缓解失真问题（或者说是让模型适应比较拥挤的位置编码）。

transformers库对于PI的实现也是非常简单，可以看到，相比原始的RoPE，简单的将position_ids除了一个内插因子$s$。有相关论文表明，即使PI+后期fintune，最多也只能外推8倍的长度，再高性能便开始下降了。

class LlamaLinearScalingRotaryEmbedding(LlamaRotaryEmbedding):"""LlamaRotaryEmbedding extended with linear scaling. Credits to the Reddit user /u/kaiokendev"""def forward(self, x, position_ids):# difference to the original RoPE: a scaling factor is aplied to the position idsposition_ids = position_ids.float() / self.scaling_factorcos, sin = super().forward(x, position_ids)return cos, sin

进一步理解位置编码高频外推与低频内插的含义

PI方法简单粗暴，但也存在很多缺点：

• 从position_id的角度理解，就是如上文所说的降低了模型的分辨率，造成局部失真。
• 从LLM中的RoPE位置编码代码解析与RoPE的性质分析（一）中的高频低频角度理解，PI方法没有考虑到高频分量和低频分量的特性，统一的对所有分量进行了内插。好的RoEP扩展方法应当是做到：高频外推、低频内插。

在LLM中的RoPE位置编码代码解析与RoPE的性质分析（一）的最后，简单介绍过高频外推与低频内插。

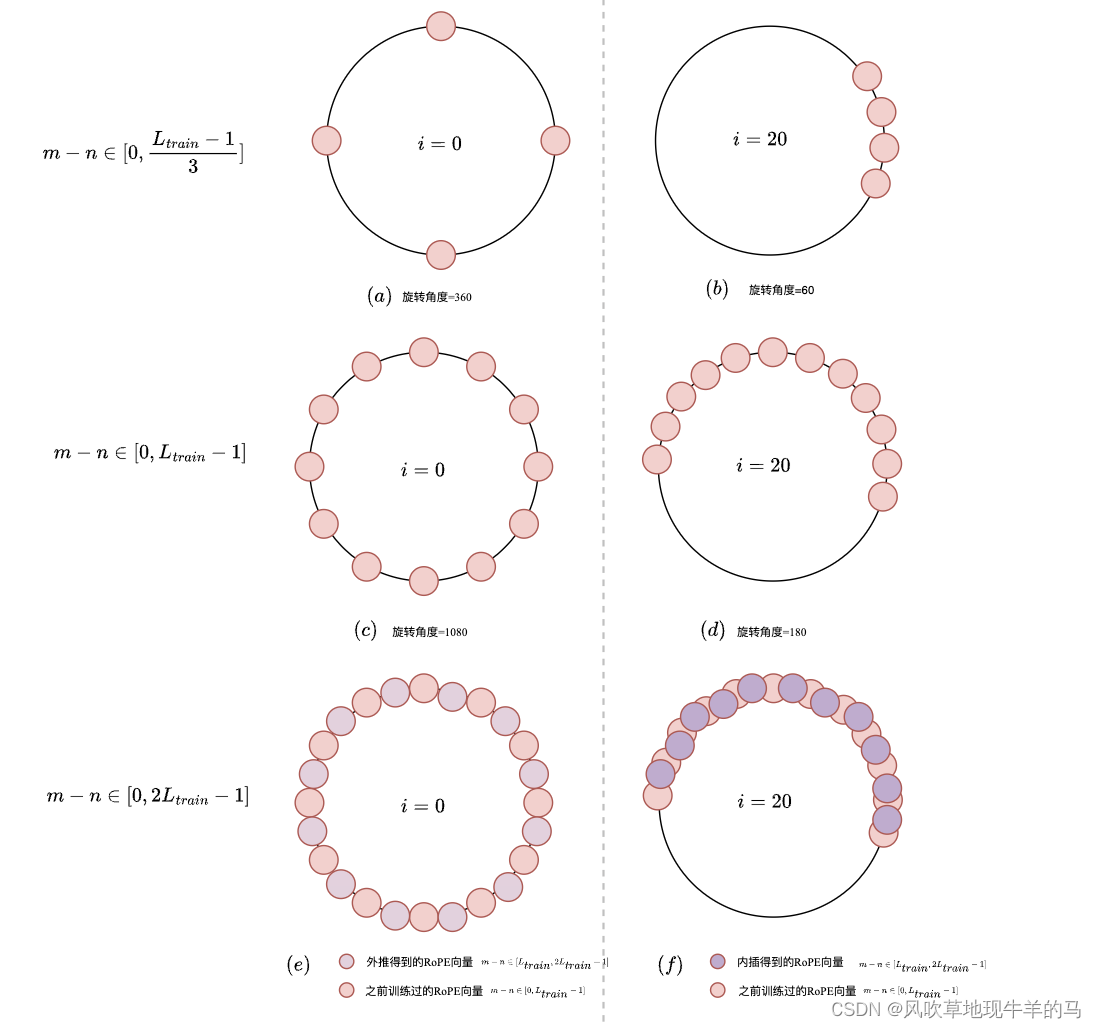
在上图中，我们说到第$i=0$组属于高频分量，此时整个圈上的每一段弧线都被训练过，所以可以直接外推（这里外推的含义就是当$m\in [L_{train},2L_{train}-1]$，不需要对$f(m,{\theta }_0)$做任何改动，可以直接扩展）。第$i=20$组属于低频分量，需要内插（这里内插的含义就是当$m\in [L_{train},2L_{train}-1]$时，需要缩放到$[0,L_{train}-1]$，此时$f$函数变为$f(m/s,{\theta }_{20}),这里缩放因子s=2$）。

也就是说，好的RoPE扩展方法，应该是当$m\in [L_{train},2L_{train}-1]$时：
$$f(m,{\theta }_i)=\{\begin{array}{rl}& f(m,{\theta }_i),i\in {\varphi }_{high}\\ & f(m/s,{\theta }_i),i\in {\varphi }_{low}\end{array}(3)$$
其中，${\varphi }_{high}$属于高频分量集合，${\varphi }_{low}$属于低频分量集合。可见PI的方法对低频分量做到了内插，但没有对高频分量做到外推。

那么对于低频分量来说，将$m/s$，本质上其实还是扩大了$base$参数，我们令

$$\frac{m}{{\widehat{base}}^{2i/d}}=\frac{m/s}{bas{e}^{2i/d}}(4)$$
解得，$\widehat{base}=s^{d/2i}base$，也就是将base参数扩大了$s^{d/2i}$倍。

ABF(增加base参数，Adjusted Base Frequency）

Effective Long-Context Scaling of Foundation Models

如何理解简单粗暴的修改base参数就可以增加模型的外推能力？

在实验中，我们发现，LLaMA3的base=10000，只能从8k直接外推到9k左右，而Qwen1.5的base=1000000，可以从32k直接外推到52k。

• 角度1：从远程衰减性的角度
  LLM中的RoPE位置编码代码解析与RoPE的性质分析（一）中提到，RoPE具有远程衰减性，当base参数较小时（比如10000），这时对于长文本来说，远程的token注意力就更减弱了，因此这篇文章中提出，可以直接将base参数从10000 增加到 500000，这样可以降低RoPE的远程衰减性。

• 角度2：从容量的角度
  如下图所示，左侧的图表示，用3维4进制的数，最多可以表示$[0-63]$，我们用$f(base=4,dim=3)$表示。
  假设现在需要表示$[0,124]$，应该如何做？当然可以继续按照4进制，将维数由3维扩展为4维。也可以有另外的方法，将进制改为5进制，这样可以在不增加维数的情况下，增加$f$的表示容量。$f(base=4,dim=3)$的容量是64，而$f(base=5,dim=3)$的容量是125。
  
  对于RoPE来说，增加base参数，相当于增加了RoPE的表示容量，所以在长度外推的时候，大的base参数，外推能力要好于小base参数的外推能力，并且，增加base参数，并不会改变相邻两个点的距离，所以不会有PI方法的局部失真问题，如论文中的图所示。
  

NTK-RoPE (NTK-aware)

https://www.reddit.com/r/LocalLLaMA/comments/14mrgpr/dynamically_scaled_rope_further_increases/

ABF的方法明显是对模型的长文本处理是有效果的，但是并没有给出一个具体计算扩大原本base的公式，NTK-RoPE给出了扩大base参数的公式：
$$f(m,{\theta }_i)=\frac{m}{(base\ast s^{d/(d-2)}{)}^{2i/d}}(5)$$
相比于公式（2），base参数被扩大了$s^{d/d-2}$倍。那么base参数为什么要扩大这么多倍？NTK-RoPE的作者提出，在推导的时候，先是保证了让最低频($i=d/2-1$)执行完整的内插。也就是有：
$$(base\ast k{)}^{-2i/d}=s\ast bas{e}^{-2i/d}$$
解得$k=s^{d/(d-2)}={\frac{L_{test}}{L_{train}}}^{d/(d-2)}$。在这种情况下，虽然NTK-RoPE对于每一个分量，都将base参数扩大了$s^{d/d-2}$倍，但是保证了最高频($i=0时，f(m,{\theta }_0)结果不变$)，从而实现了最高频外推（不插值），最低频($i=d//2-1$)插值，从而在免训练的情况下，效果超过了PI。

但是在微调情况下，PI的效果要好于NTK-RoPE，原因在于NTK-RoPE可能会出现越界值，缓解的办法是，调高$s$

代码实现如下：

class LlamaDynamicNTKScalingRotaryEmbedding(LlamaRotaryEmbedding):"""LlamaRotaryEmbedding extended with Dynamic NTK scaling. Credits to the Reddit users /u/bloc97 and /u/emozilla"""def forward(self, x, seq_len):# difference to the original RoPE: inv_freq is recomputed when the sequence length > original lengthposition_ids = torch.arange(seq_len, dtype=torch.int64).unsqueeze(0).to(x.device)# seq_len = torch.max(position_ids) + 1if seq_len > self.max_position_embeddings:base = self.base * ((self.scaling_factor * seq_len / self.max_position_embeddings) - (self.scaling_factor - 1)) ** (self.dim / (self.dim - 2))inv_freq = 1.0 / (base ** (torch.arange(0, self.dim, 2, dtype=torch.int64).float().to(x.device) / self.dim))self.register_buffer("inv_freq", inv_freq, persistent=False)  # TODO joao: this may break with compilationcos, sin = super().forward(x, position_ids)return cos, sin

目前所有的非Dynamic的长度扩展方法均会对$L_{train}$长度内的文本性能造成一定下降。为了避免外推的时候，影响$L_{train}$长度内的文本性能表现，上面的代码使用了Dynamic的方法。

Yarn (NTK-by-parts)

YaRN: Efficient Context Window Extension of Large Language Models
这篇论文写的很好，建议阅读。

NTK-RoPE的方法只保证了最高频分量外推和最低频分量内插。根据公式（3），应该是对高频分量集合${\varphi }_{high}$外推，对低频分量集合${\varphi }_{low}$内插。那么如何得到${\varphi }_{high}$和${\varphi }_{low}$？

这里需要额外引入一个概念，波长$\lambda$，我们定义RoPE embedding的第$i$组分量的波长计算公式：
$${\lambda }_i=\frac{2\pi }{{\theta }_i}=2\pi bas{e}^{2i/d}(6)$$
公式（6）描述了RoPE的第$i$组分量旋转360度（一圈）所走过的长度。Yarn论文的作者还发现，对于某些低频分量，其波长${\lambda }_i>L_{train}$，也就是如我们前面所讲的，在整个训练过程中，没有转够一圈，整个圈上只有一段弧线被训练过。对于高频分量来说，可能已经转了很多圈。所以我们还可以定义一个在$L_{train}$长度上的圈数：
$$r_i=\frac{L_{train}}{{\lambda }_i}$$
那么，我们可以定义两个超参数，${\beta }_{fast}$与${\beta }_{slow}$，分别表示筛选高频分量的阈值与筛选低频分量的阈值：

• 若$r_i>{\beta }_{fast}$，那么认为是高频分量，不需要内插。
• 若$r_i<{\beta }_{slow}$，那么认为是低频分量，需要内插。
• 若介于二者之间，则内插和外推均可。

若用公式来表达，那就是：

$$f(m,{\theta }_i)=\frac{m/s}{bas{e}^{2i/d}}(1-\alpha (r_i))+\frac{m}{bas{e}^{2i/d}}\alpha (r_i)(7)$$
其中：
$$\alpha (r_i)=\{\begin{array}{rl}& 1,r_i>{\beta }_{fast}\\ & 0,r_i<{\beta }_{slow}\\ & \frac{r_i-{\beta }_{slow}}{{\beta }_{fast}-{\beta }_{slow}},{\beta }_{slow}<=r_i<={\beta }_{fast}\end{array}(8)$$

1. 截止目前，其实都是NTK-by-parts的内容。
2. NTK-by-parts在微调和非微调的场景下，均取得了最好的性能。
3. 在论文中，作者发现对于LLaMA2来说，${\beta }_{fast}=32,{\beta }_{slow}=1$时，可以有最好的性能表现。

下图展示了LLaMA2-7B的不同分量对应的旋转圈数的变化曲线，${\beta }_{fast}=32,{\beta }_{slow}=1,i\in [0,2048)$。

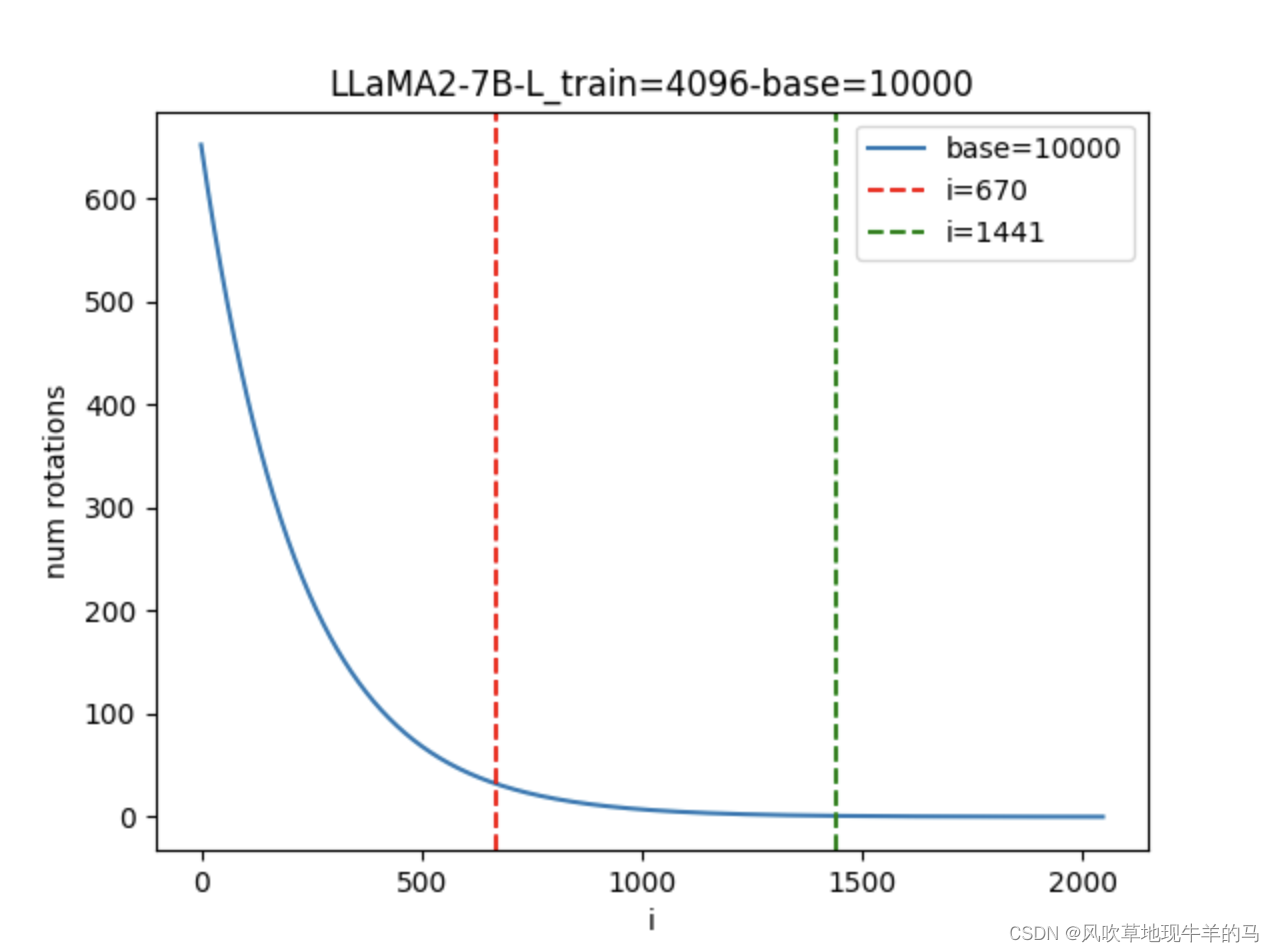
• $i=670$左侧的区域均直接外推，不进行插值
• $i=1441$右侧的区域进行内插
• 中间的区域外推和内插混合。

制图的代码如下

import torch
import math
import matplotlib.pyplot as pltdef find_correction_dim(num_rotations, dim, base=10000, max_position_embeddings=2048):return (dim * math.log(max_position_embeddings/(num_rotations * 2 * math.pi)))/(2 * math.log(base))# Find dim range bounds based on rotations
def find_correction_range(beta_fast, beta_slow, dim, base=10000, max_position_embeddings=2048):low = math.floor(find_correction_dim(beta_fast, dim, base, max_position_embeddings))high = math.ceil(find_correction_dim(beta_slow, dim, base, max_position_embeddings))return max(low, 0), min(high, dim-1)  # Clamp values just in casedim = 4096
max_pos_embeddings = 4096
base = 10000
inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2) / dim))# 波长
lambda_ = 2 * math.pi / inv_freq
# 旋转圈数
num_ros = max_pos_embeddings / lambda_x = torch.arange(dim//2).numpy()
y = num_ros.numpy()low_dim, high_dim = find_correction_range(beta_fast=32, beta_slow=1, dim=dim, base=base, max_position_embeddings=max_pos_embeddings)
print(low_dim)
print(high_dim)
print(num_ros[high_dim], num_ros[low_dim])plt.title(f'LLaMA2-7B-L_train={max_pos_embeddings}-base={base}')
plt.plot(x, y,  label=f"base={base}")
plt.axvline(x=low_dim, color="r", linestyle='--', label=f'i={low_dim}')
plt.axvline(x=high_dim, color="g", linestyle='--', label=f'i={high_dim}')
plt.legend()
plt.xlabel('i')
plt.ylabel('num rotations')
plt.show()

接下来应该是Yarn的版本了。Yarn是在NTK-by-parts的基础上，在计算attention score的时候，进行了一个温度系数的惩罚。
$$softmax(\frac{q_m{k}_n^T}{t\sqrt{d}})$$
由于RoPE的特性，直接将$q_m与k_n$除以$\sqrt{1/t}$，可以达到同样的效果。那么$\sqrt{1/t}$如何确定？Yarn论文作者取值为：
$$\sqrt{1/t}=0.1ln(s)+1$$

至此，Yarn的方法就结束了。
Yarn的代码如下：

class LlamaYaRNScaledRotaryEmbedding(LlamaRotaryEmbedding):def __init__(self,*args,original_max_position_embeddings=2048,extrapolation_factor=1,attn_factor=1,beta_fast=32,beta_slow=1,device=None,**kwargs):super().__init__(*args, **kwargs)self.original_max_position_embeddings = original_max_position_embeddingsself.extrapolation_factor = extrapolation_factorself.attn_factor = attn_factorself.beta_fast = beta_fastself.beta_slow = beta_slowself.yarn(device)def yarn(self, device):pos_freqs = self.base ** (torch.arange(0, self.dim, 2).float().to(device) / self.dim)inv_freq_extrapolation = 1.0 / pos_freqsinv_freq_interpolation = 1.0 / (self.scaling_factor * pos_freqs)# beta_fast和beta_slow表示分量旋转弧度的阈值，意思就是分量d的旋转弧度大于beat_fast，可以认为整个圈上的每个点都训练充分了，直接外推# 分量d的旋转弧度小于beta_slow，可以认为是整个圈上，只有一段弧线被训练过，需要内插low, high = find_correction_range(self.beta_fast, self.beta_slow, self.dim, self.base, self.original_max_position_embeddings)# 对应yarn论文的公式（13）inv_freq_mask = (1 - linear_ramp_mask(low, high, self.dim // 2).float().to(device)) * self.extrapolation_factor  # Get n-d rotational scaling corrected for extrapolationinv_freq = inv_freq_interpolation * (1 - inv_freq_mask) + inv_freq_extrapolation * inv_freq_maskself.register_buffer("inv_freq", inv_freq)self.mscale = float(get_mscale(self.scaling_factor) * self.attn_factor)   # Get n-d magnitude scaling corrected for interpolationdef forward(self, x, seq_len=None):# x: [bs, num_attention_heads, seq_len, head_size]# This `if` block is unlikely to be run after we build sin/cos in `__init__`. Keep the logic here just in case.cos, sin = super().forward(x, seq_len)cos = cos * self.mscalesin = sin * self.mscalereturn cos, sin

目前开源厂家如何增强LLM的长文本能力

Yi

根据Yi的技术报告，Yi的方案是：

1. 训练4k 预训练模型 ，base=10000
2. 修改base为10000000，max_position_embeddings=32768，在长文本（数据来源于书籍，长度可能是16k、32k）上少量训练，1-2Btoken就可收敛
3. 外推到200k（不用任何长度扩展技术？根据目前开源的checkpoint是这样的。）

InternLM

根据InternLM的技术报告，InterLM的方案是：

1. 训练4k 预训练模型，base=50000
2. 修改base=1000000，max_position_embeddings=32768，混合50%的32k数据继续训练。
3. 外推到200k

qwen1.5

qwen1.5没有技术报告，但是可以从config.json中看到，qwen1.5的max_position_embeddings=32768，达到了32k，base=1000000，方案可能和Yi、InternLM的类似。
在我们的测试下，qwen1.5直接外推可以到52k长度，yarn可以扩展到128k。

参考文献：
https://spaces.ac.cn/archives/9948/comment-page-2#comments
https://blog.csdn.net/PennyYu123/article/details/131717323
https://openreview.net/pdf?id=wHBfxhZu1u

这篇关于一文看懂如何增强LLM的长文本处理能力（包含代码和原理解析）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---