本文主要是介绍【动态规划】C++解决01背包问题(模板01背包、分割等和子集、目标和、最后一块石头的重量),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1. 前言
- 2. 算法题
- 2.1_【模板】01背包
- 2.2_分割等和子集
- 2.3_目标和
- 2.4_最后一块石头的重量II
1. 前言
关于 动态规划的理解 与例题,点击👇
【动态规划】C++解决斐波那契模型题目(三步问题、爬楼梯、解码方法…)
有了上面的经验,我们来解下面 01 背包问题
2. 算法题
2.1_【模板】01背包

思路
-
设置状态表示
- 对于此类背包问题,我们需要考虑的因素往往不止一个,状态表示会根据影响结果的因素而定
- dp[i][j]:从前i个物品进行选择,所选体积不超过j的最大价值
-
写状态转移方程
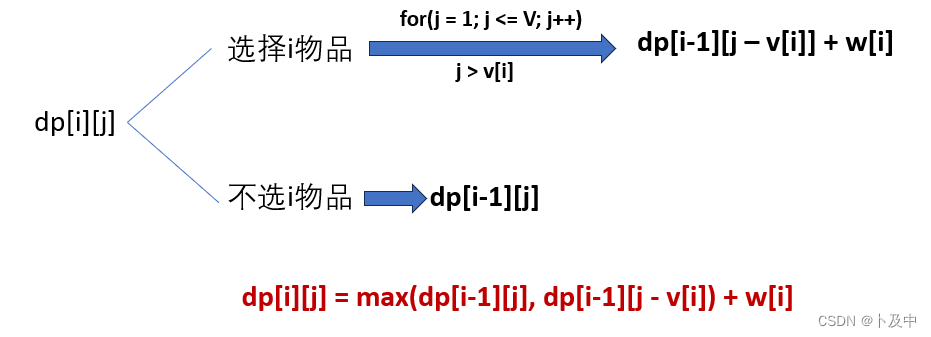
-
初始化
- 虚拟空间一行一列,并初始化为0(因为会用max更新dp值)
-
填表的顺序
- 从上向下 填表即可
-
返回值
- dp[n][V]
代码
#include <iostream>
#include <string>using namespace std;// 定义全局变量 自动初始化为0
const int N = 1001;
int w[N], v[N], n , V; // n个物品 体积为V
int dp[N][N]; // dp数组: 自动初始化为0// 01背包
int main()
{// 读数据cin >> n >> V;for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];// 第一问// dp[i][j]:从前i个物品进行选择,所选体积不超过j的最大价值for(int i = 1; i <= n; ++i)for(int j = 1; j <= V; ++j){dp[i][j] = dp[i-1][j]; // 不选i物品if(j >= v[i])dp[i][j] = max(dp[i][j], dp[i-1][j-v[i]] + w[i]); }cout << dp[n][V] << endl;// 第二问// 初始化dpfor(int j = 1; j <= V; ++j) dp[0][j] = -1; // -1表示无效选法// 填表for(int i = 1; i <= n; ++i)for(int j = 1; j <= V; ++j){dp[i][j] = dp[i-1][j]; // 不选i物品if(j >= v[i] && dp[i-1][j-v[i]] != -1)dp[i][j] = max(dp[i][j], dp[i-1][j-v[i]] + w[i]); }cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}2.2_分割等和子集

思路
- 题意分析
- 题目要求判断是否可以将数组分割成两个元素和相同的子集,即每个子集的元素和为sum(数组总和) / 2
- 我们可以对题目进行转化,即只要能在数组中找到子集使其和为sum/2,那么就一定有另一个和自己元素和相同的子集
- 即在数组中找到和为sum/2的元素选法个数,即01背包
-
设置状态表示
- 根据题目,要求判断是否可以将数组分割,所以dp表类型设置为bool
- dp[i][j]:以i为结尾的子数组中所有的选法中,是否有总和为j的
-
写状态转移方程
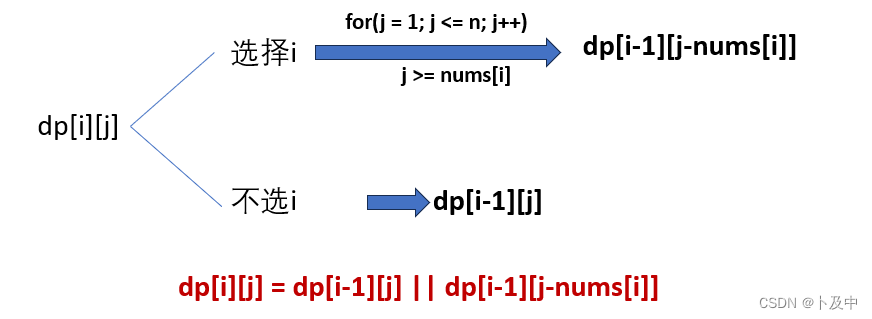
-
初始化
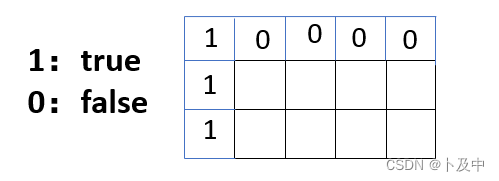
-
填表的顺序
- 从上向下填写每行
-
返回值
- dp[n][sum/2]
代码
class Solution {
public:bool canPartition(vector<int>& nums) {// 题目转化:找数,使和为sum/2int sum = 0, n = nums.size();for(auto num : nums) sum += num; // 数组和if(sum % 2 == 1) return false; // 奇数,不能分割int aim = sum / 2;// 创建dp数组:dp[i][j]: 以i为结尾的子数组中,总和是否为jvector<vector<bool>> dp(n+1, vector<bool>(aim+1));// 初始化 + 填表for(int i = 0; i <= n; ++i) dp[i][0] = true;for(int i = 1; i <= n; ++i)for(int j = 1; j <= aim; ++j){dp[i][j] = dp[i-1][j]; // 不选i位置数if(j >= nums[i-1]) // 映射下标dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];}return dp[n][aim];}
};
2.3_目标和

思路
- 题意分析
- 根据题目,即由x个正数与y个负数可以组成目标值target
- 那么有:x - y = target,x + y = sum(数组和)
- 则 x = (target + sum) / 2
- 此时题目可以理解成,从数组中选择数,数的总和为x,求总共的选法,即01背包:
- 设置状态表示
- dp[i][j]:以i为结尾的子数组中和为j的选法的个数
- 写状态转移方程
- 可以看出本题与上题的总体差别不大,根据状态表示的不同,状态转移方程和初始化进行简单改动:
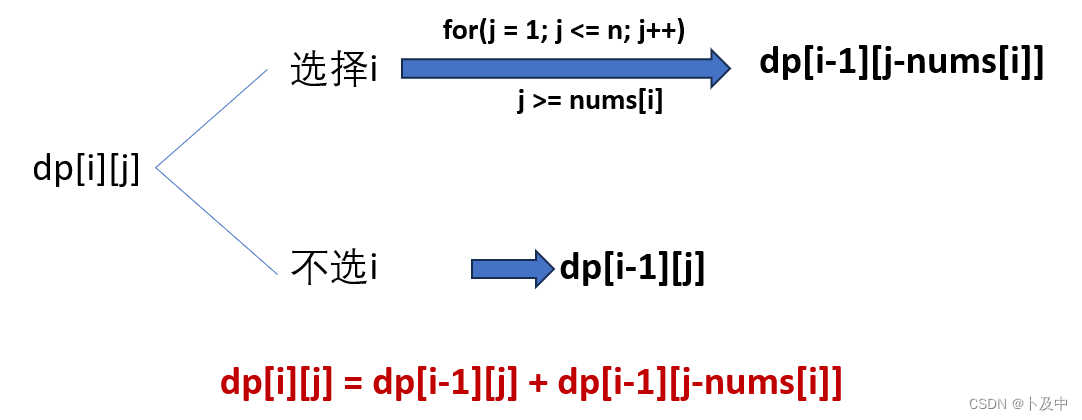
-
初始化
- 只需要初始化第一行,dp[0][0] = 0,dp[0][j] = 1(j >= 1)
-
填表的顺序
- 从上向下
-
返回值
- dp[n][aim]
代码
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {// 题目转化:从数组中选择一些数,使其和为目标值,求选法的个数int n = nums.size(), sum = 0; // 数组和for(auto x : nums) sum += x;// a: 正数和 b: 负数和(绝对值)// a + b = sum; a - b = targetint aim = (sum + target) / 2; if(aim < 0 || (sum + target) % 2 == 1) return 0; // 处理边界条件// 创建 + 初始化vector<vector<int>> dp(n+1, vector<int>(aim + 1));dp[0][0] = 1;for(int i = 1; i <= n; ++i)for(int j = 0; j <= aim; ++j){dp[i][j] = dp[i-1][j]; // 不选i位置数if(j >= nums[i-1]) dp[i][j] += dp[i-1][j-nums[i-1]];}return dp[n][aim];}
};
2.4_最后一块石头的重量II
思路
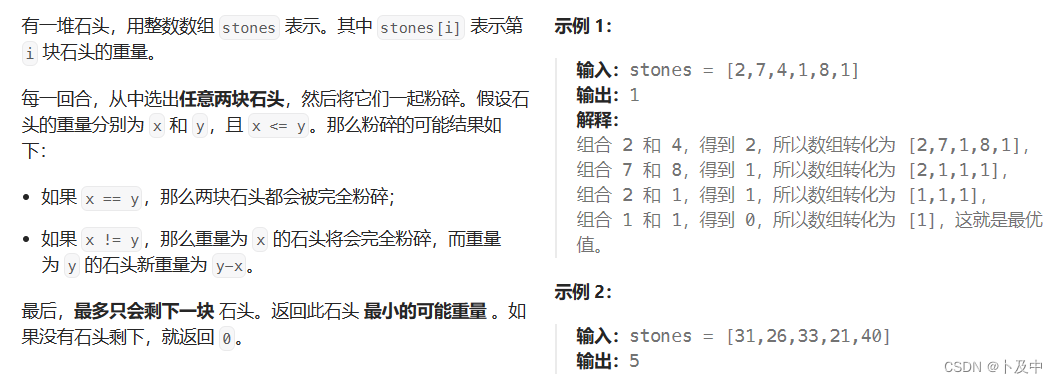
- 题意分析
- 观察题目,石头碰撞的过程实际就是,两个数相减的过程;
- 要想使最后的重量最小,只需要在数组中找到序列总和尽可能接近sum/2,此时与剩下的相减的值就是最小的
- 即转化为了01背包问题;
-
设置状态表示
- dp[i][j]:以i为结尾的子数组中,总和不大于j的最大和(<=j)
-
写状态转移方程
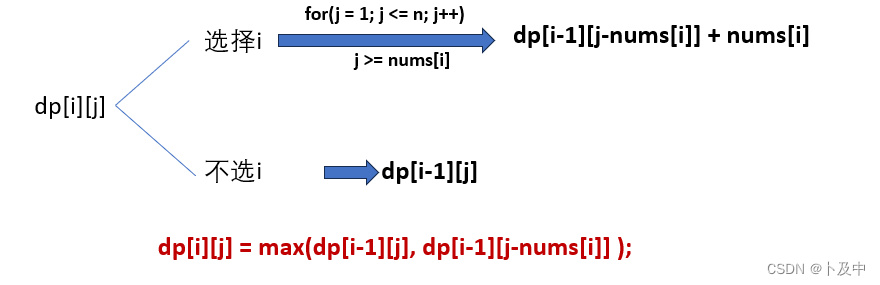
-
初始化
- 初始化第一行为0
-
填表的顺序
- 从上往下
-
返回值
- sum - (2*dp[n][sum / 2])
代码
int lastStoneWeightII(vector<int>& stones) {// 题目转化为: 在数组中选数,使其总和最接近sum/2int sum = 0, n = stones.size();for(auto x : stones) sum += x;int aim = sum / 2;// 创建dp数组: dp[i][j]:从前i个数中选数,使其和最接近j时的值vector<vector<int>> dp(n+1, vector<int>(aim+1));for(int i = 1; i <= n; ++i)for(int j = 0; j <= aim; ++j){dp[i][j] = dp[i-1][j]; // 不选i数if(j >= stones[i-1]) dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i-1]] + stones[i-1]);}return sum - 2*dp[n][aim];}
这篇关于【动态规划】C++解决01背包问题(模板01背包、分割等和子集、目标和、最后一块石头的重量)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



