本文主要是介绍秋招突击——算法打卡——6/3——复习{最低通行费、(状态压缩DP)小国王}——新做:{罗马数字转整数、最长公共前缀},希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 复习
- 背包模型——最低通行费
- 题目内容
- 实现代码
- (状态压缩DP)小国王
- 检查状态本身是否存在两个连续的1
- 计算所有的合法状态已经所有合法状态之间的转移
- 动态规划过程
- 新作
- 罗马数字转整数
- 个人实现
- 实现代码
- 参考做法
- 实现代码
- 最长公共前缀
- 个人实现
- 参考思路
- 总结
复习
背包模型——最低通行费
题目内容

实现代码
- 首先规定了步数是2n-1,相当于只能往右下那个方向出发,只能往下或者往右走
- 最小花费,那么f[i][j],就表示到达第i和j的格子中若干方案中最低的代码。
- 完全可以使用动态规划,但是边界条件确定还是有点问题,并不知道怎么弄。
- 真牛,我还不确定这样写对不对,结果跟参考代码写的一模一样。
- 就是从最初的那个单元格进行遍历,发现有一个单元格始终是空的,所以就对那个单元格进行赋值就行了,然后再往下继续便利赋值即可。
#include <iostream>
#include <algorithm>using namespace std;
const int N = 110;
int w[N][N],f[N][N];
int n;
int main(){cin>>n;// 记录矩阵信息for (int i = 1; i <= n ; ++i) {for (int j = 0; j <= n ; ++j) {cin>>w[i][j];}}// 根据状态转换方程进行变动 f[i][j] = max(f[i - 1][j],f[i][j - 1]) + w[i][j]for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {if (i == 1 && j == 1) f[i][j] = w[i][j];else f[i][j] = INT_MAX;if (i - 1 >= 0) f[i][j] = min(f[i][j],f[i -1][j]) + w[i][j];if (j - 1 >= 0) f[i][j] = min(f[i][j],f[i][j - 1]) + w[i][j];}}cout<<f[n][n]<< endl;
}
(状态压缩DP)小国王
- 上半场题解链接
- 上次讲到要验证状态是否合法,所以需要写一下状态合法的判定情况,然后在计算一下有哪些状态是合法,那些状态转换是合法的。
检查状态本身是否存在两个连续的1
- 实际上可以使用错位相与,不等于零就是错的
bool check(int state){// 检查是否存在连续的两个一,如果存在就是不合法for(int i = 0;i < n;i ++)if ((state >> i & 1) && (state >> i + 1 & 1))return false;return true;
}

- 可以改成如下形式
bool check(int state){// 检查是否存在连续的两个一,如果存在就是不合法return !(state & (state >> 1));
// for(int i = 0;i < n;i ++)
// if ((state >> i & 1) && (state >> (i + 1) & 1))
// return false;
// return true;
}
计算所有的合法状态已经所有合法状态之间的转移
- 这里每一行有n个格子,每一个格子是两种状态,相当于是2的n次方,所以移位运算就是乘以2倍数。遍历所有状态就是可以的。
- 这里判定两个状态是否是合法,需要好好画一下图,具体如下
- a:100101
- b:010000
- 按位或:110101,如果他出现相邻的1,就是不合格的状态,所以需要进行判定。
// 这里是遍历所有的情况,并将所有的状态保存起来for (int i = 0; i < 1 << n; ++i) {if (check(i)){state.push_back(i);id[i] = state.size() - 1; // 存储每一个合法状态的坐标cnt[i] = count(i); // 计算当前合法状态中1的个数,也就是国王的个数}}
// 这里是相邻两种状态能不能实现转移的判定条件,就是相同的位置不能为一,交叉位置不能为1.for (int i = 0; i < state.size(); ++i) {for (int j = 0; j < state.size(); ++j) {int a = state[i], b = state[j]; // 统计两个合法状态if ((a & b) == 0 && check(a | b)) // 不能有交集,并且不能有斜插head[a].push_back(b); // 保存a所有能够转移的合法的b的状态}}
动态规划过程
- 需要理解这个动态规划的坐标f[i][j][k]
- i:表示第i行
- j:表示总共放j个国王
- k:表示第k个状态
f[0][0][0] = 1;
// 这里是总共有n行,然后逐行进行遍历
for (int i = 1; i <= n + 1; ++i) {// 假设一开始是要求放j个国王for (int j = 0; j <= m ; ++j) {// 遍历当前位置所有的合法情况for (int a = 0; a < state.size(); ++a) {// 遍历当前位置的所有合法情况for (int b:head[a]) {int c = cnt[state[a]];if (j >= c){f[i][j][a] += f[i - 1][j - c][b];}}}}
}cout<<f[n + 1][m][0];
新作
罗马数字转整数
题目链接
个人实现
- 数字转罗马,就是中等,从罗马转数字,就是中等
- 正常进行遍历,遇到不同的数字进行不同的操作
- 特殊情况,如果右边的数字比左边的大,那就执行特殊情况,想减
实现代码
- 不知道如何往unordered_map中添加多个元素
方法一:std::unordered_map<std::string, int> umap;// 使用insert方法和initializer_list一次性添加多个元素umap.insert({{"one", 1},{"two", 2},{"three", 3}});方法二:std::unordered_map<std::string, int> umap = {{"one", 1},{"two", 2},{"three", 3}};
- string.at返回的是string还是char?
- 返回的是char型数据
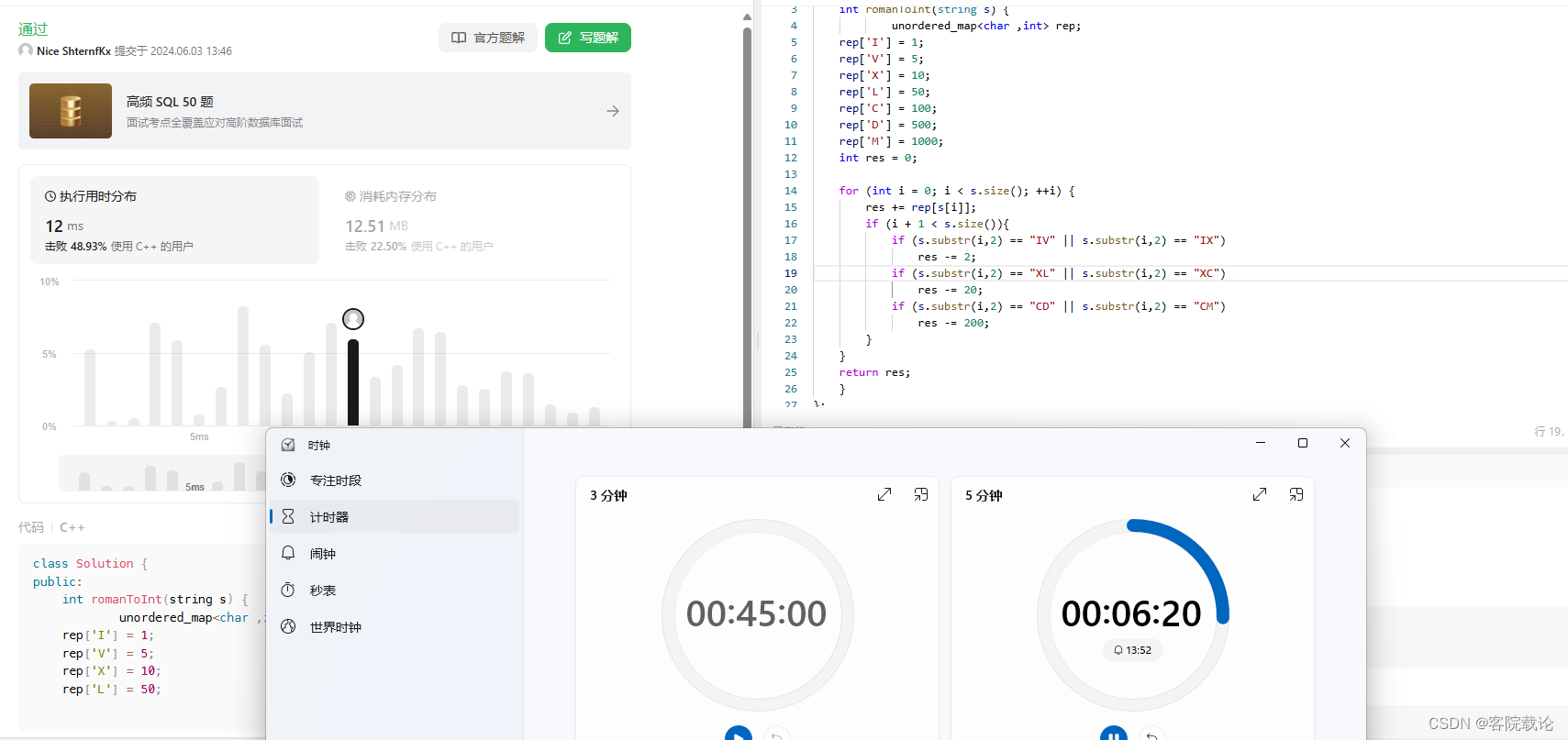
#include <iostream>
#include <string>
#include <unordered_map>using namespace std;int romanToInt(string s){unordered_map<char ,int> rep;rep['I'] = 1;rep['V'] = 5;rep['X'] = 10;rep['L'] = 50;rep['C'] = 100;rep['D'] = 500;rep['M'] = 1000;int res = 0;for (int i = 0; i < s.size(); ++i) {res += rep[s[i]];if (i + 1 < s.size()){if (s.substr(i,2) == "IV" || s.substr(i,2) == "IX")res -= 2;if (s.substr(i,2) == "Xl" || s.substr(i,2) == "XC")res -= 20;if (s.substr(i,2) == "CD" || s.substr(i,2) == "CM")res -= 200;}}return res;
}int main(){cout<<romanToInt("MMMXLV");
}
参考做法
- 这里是判定,当前数字是大于等于下一个数字,就是默认直接替换,如果小于,那就减去当前的数字,具体实现方式如下
实现代码
#include <iostream>
#include <string>
#include <unordered_map>using namespace std;int romanToInt(string s){unordered_map<char ,int> rep = {{'I',1},{'V',5},{'X',10},{'L',50},{'C',100},{'D',500},{'M',1000}};int res = 0;for (int i = 0; i < s.size(); ++i) {if (i + 1 < s.size() && s[i] < s[i + 1])res -= rep[i];else res += rep[i];}return res;
}int main(){cout<<romanToInt("MMMXLV");
}
最长公共前缀
题目链接
- 一看就知道是动态规划,那是最长公共子序列
个人实现
- 具体一看,这道题并不是动态规划,应该是简单版的,直接遍历就行了,具体实现代码如下
- 直接那第一个字符串,然后遍历第一个字符串的所有字符,然后和后续所有的字符串比较,相同跳过,不同直接突出,返回。如果是自然到末尾,就是需要加一。
class Solution {
public:string longestCommonPrefix(vector<string>& s) {if (s.size() == 1) return s[0];int r = 0;bool flag = true;for(int i = 0;i < s[0].size();i ++){r = i;for(int j = 1;j < s.size();j ++){if(i < s[j].size() && s[0][i] == s[j][i])continue;else{flag = false;break;}}if(!flag) break;}if (flag)return s[0].substr(0,r + 1);elsereturn s[0].substr(0,r);}
};
参考思路
- 思路是一样的,但是他的代码比我的简洁,是这样的,直接遍历所有的i,然后获取第一个字符串的i,然后在判定其他的,相同再加上去,不同的话,直接返回
class Solution {
public:string longestCommonPrefix(vector<string>& s) {if (s.size() == 1) return s[0];string r;for (int i = 0; ; ++i) {if (i >= s[0].size()) return r;char t = s[0][i];for (int j = 1; j < s.size(); ++j) {if (t != s[j][i]) return r;}r += t;}}
};

总结
- 今天这道题DP问题就花了很多时间,完全就没有必要,所以下次还是规定一下时间超过了,就明天再来。
- 今天两道简单题,还行。
这篇关于秋招突击——算法打卡——6/3——复习{最低通行费、(状态压缩DP)小国王}——新做:{罗马数字转整数、最长公共前缀}的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







