C语言Prim算法和Prim-Alternat找最小生成树

本文主要是介绍C语言Prim算法和Prim-Alternat找最小生成树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

- 1、用prim算法求最小生成树
- - C语言Prim算法实现
- 2、用Prim-Alternate算法求最小生成树
- - 3、C语言Prim-Alternate算法实现

1、用prim算法求最小生成树

绿色线会标记选过的边

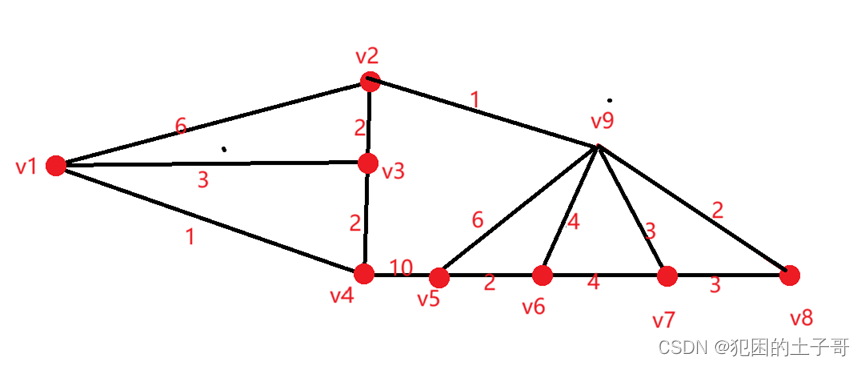
在这里插入图片描述

从v1当作起始点开始，可选择:
(v1,v2)权值为6
（v1,v3）权值为3
（v1，v4）权值为1
从中选择边（v1，v4），最小权值为1
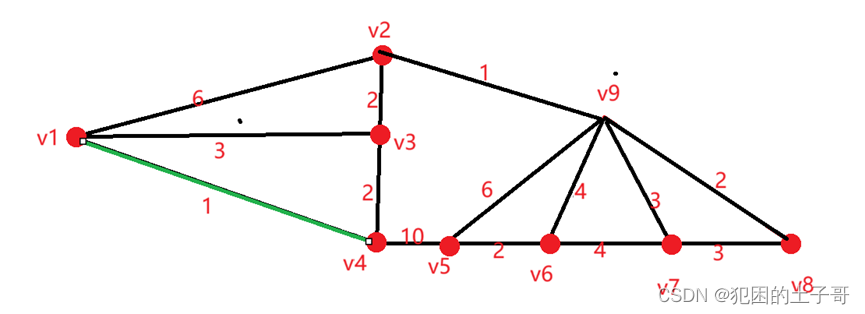
在这里插入图片描述

从v1和v4中选连接边，可选择的边有：
（v1，v2）权值为6
（v1,v3）权值为3
（v4，v3）权值为2
（v4，v5）权值为10
从中选择权值最小为2的边，（v4，v3）
在这里插入图片描述

v1，v4，v3已经被标记不能相互连接，避免产生回路，从v1、v4、v3中可选择的边有：
（v1，v2）权值为6
（v4，v5）权值为10
（v3，v2）权值为2
从中选择权值最小为2的边，（v3，v2）
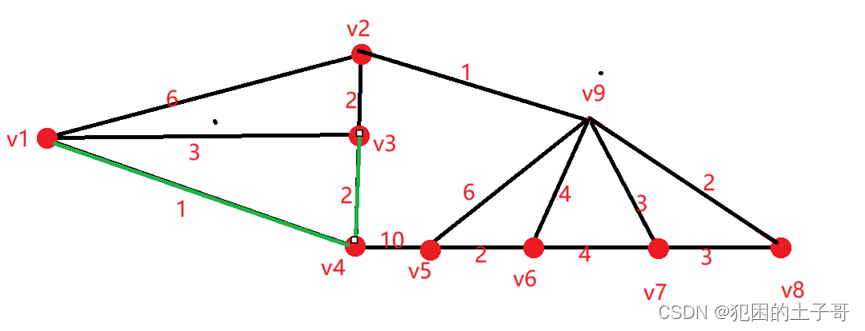
在这里插入图片描述

从v1,v4,v3,v2中可选择的边有：
（v2，v9）权值为1
（v4，v5）权值为10
从中选择权值最小1的边，（v2，v9）
在这里插入图片描述

从v1，v4，v3，v2，v9中可选边有：
（v4，v5）权值为10
（v9，v5）权值为 6
（v9，v6）权值为 4
（v9，v7）权值为 3
（v9，v8）权值为 2
从中选择权值最小2的边，（v9，v8）
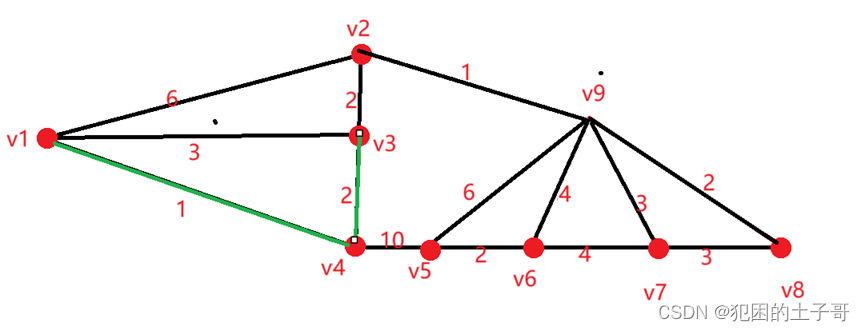
在这里插入图片描述

从v1，v4，v3，v2，v9，v8中可选边有：
（v4，v5）权值为10
（v9，v5）权值为 6
（v9，v6）权值为 4
（v9，v7）权值为 3
（v8，v7）权值为 3
从中有两条权值为3的边，任选一条（v8，v7）
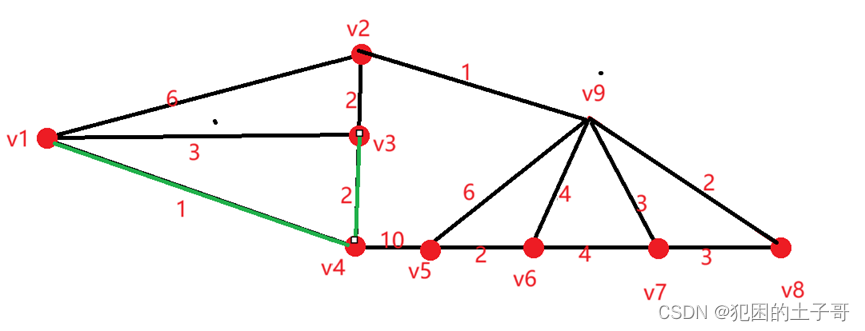
在这里插入图片描述

从v1，v4，v3，v2，v9，v8，v7中可选边有：
（v4，v5）权值为10
（v9，v5）权值为 6
（v9，v6）权值为 4
（v7，v6）权值为 4
从两条权值为4的边，任选一条（v7，v6）
在这里插入图片描述

从v1，v4，v3，v2，v9，v8，v7，v6中可选边有：
（v4，v5）权值为10
（v9，v5）权值为 6
（v6，v5）权值为 2
选择最小权值为2的边（v6，v5）
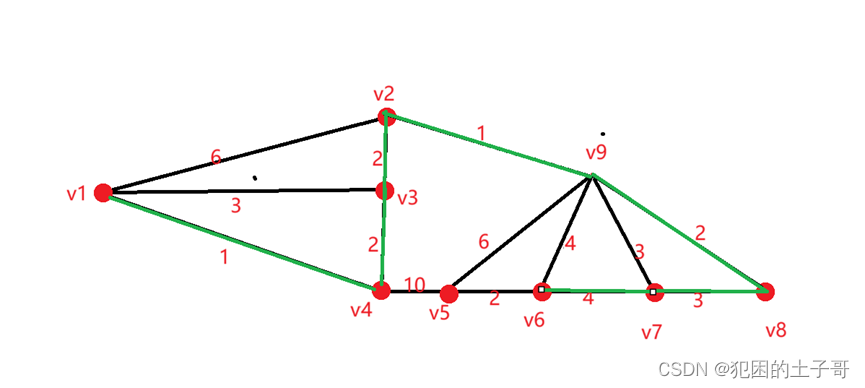
在这里插入图片描述

v1，v4，v3，v2，v9，v8，v7，v6，v5所有点被标记
最小生成树找到，总权值为17
在这里插入图片描述

C语言Prim算法实现

#include<stdio.h>
#define M 1000//M表示无穷用1000代替
//判断标记点的函数，避免产生回路
int Is(int arr[9], int flag)
{int i = 0;for (i = 0; i < 9; i++){if (arr[i] == flag)return 0;}return 1;
}
int main()
{//把上图权值对应值写成邻接阵int map[9][9] ={{M,6,3,1,M,M,M,M,M},{6,M,2,M,M,M,M,M,1},{3,2,M,2,M,M,M,M,M},{1,M,2,M,10,M,M,M,M},{M,M,M,10,M,2,M,M,6},{M,M,M,M,2,M,4,M,4},{M,M,M,M,M,4,M,3,3},{M,M,M,M,M,M,3,M,2},{M,1,M,M,6,4,3,2,M}};//存放被标记的点int arr[9] = { 1 };//设置初始点为V1，只有V1被标记//记录标记个数int count = 1;//存放权值总和int s = 0;//循环变量int i = 0;//记录最小权下标int index = 0;//记录最小权int min = M;//记录点int doc = 1;//循环部分：while (1){min = M;for (i = 0; i < count; i++){int j = 0;int c = arr[i] - 1;for (j = 0; j < 9; j++){if (map[c][j] <= min && Is(arr, j + 1)){doc = c + 1;min = map[c][j];index = j;}}}s += min;arr[count++] = index + 1;//打印printf("V%d --> V%d ", doc, index + 1);//所有点被标记，跳出循环if (count == 9)break;}printf("\n总权值为：%d\n", s);return 0;
}

运行结果:

在这里插入图片描述

2、用Prim-Alternate算法求最小生成树

Prim-Alternate算法是Prim算法的优化
Prim-Alternate算法是只找当前标记点和上一个标记点的邻边
被标记的点不能互相相连

3、C语言Prim-Alternate算法实现

//Prim-Alternate算法
#include<stdio.h>
#define M 1000//M表示无穷用1000代替
//判断标记点的函数，避免产生回路
int Is(int arr[9], int flag)
{int i = 0;for (i = 0; i < 9; i++){if (arr[i] == flag)return 0;}return 1;
}
int main()
{//把上图权值对应值写成邻接阵int map[9][9] ={{M,6,3,1,M,M,M,M,M},{6,M,2,M,M,M,M,M,1},{3,2,M,2,M,M,M,M,M},{1,M,2,M,10,M,M,M,M},{M,M,M,10,M,2,M,M,6},{M,M,M,M,2,M,4,M,4},{M,M,M,M,M,4,M,3,3},{M,M,M,M,M,M,3,M,2},{M,1,M,M,6,4,3,2,M}};//存放被标记的点int arr[9] = { 1 };//设置初始点为V1，V1被标记//记录标记个数int count = 1;//存放权值总和int s = 0;//循环变量int i = 0;//记录最小权下标int index = 0;//记录最小权int min = M;//记录点int doc = 1;int c = 0;//循环部分：while(1){min = M;
//每次循环只找两个标记点相邻的边for(i=count-2;i< count ;i++){ int j = 0;if (count == 1)c = arr[0] - 1;elsec = arr[i] - 1;for (j = 0; j < 9; j++){if (map[c][j] <= min && Is(arr, j + 1)){doc = c+1;min = map[c][j];index = j;}}}s += min;arr[count++] = index + 1;//打印printf("V%d --> V%d ",doc , index + 1);//所有点被标记，跳出循环if (count == 9)break;		}printf("\n总权值为：%d\n", s);return 0;
}