视觉SLAM位姿估计（总结）

本文主要是介绍视觉SLAM位姿估计（总结），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Overview

欢迎访问 持续更新：https://cgabc.xyz/posts/102a40b/

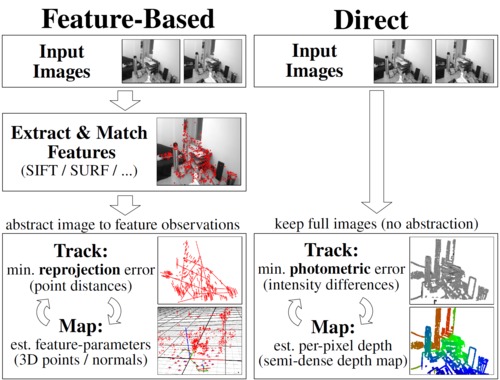
Features Based Method

2D-2D: Epipolar Geometry

2D-2D 对极几何主要涉及到基础矩阵、本质矩阵和单应性矩阵的求解，并从中恢复出旋转矩阵 $R$ 和平移向量 $t$ 。

计算机视觉对极几何之FEH

同时，还要根据匹配的特征点和计算出的相对位姿进行三角化，恢复出 3D空间点。

计算机视觉对极几何之Triangulate(三角化)

在单目视觉SLAM中，以上过程主要用于SLAM的初始化：计算第二关键帧的相对位姿（假设第一帧位姿为 $\quad 0]$ ），并计算初始Map。

OpenCV 中相关函数：

findFundamentalMat
findEssentialMat
findHomography
recoverPose
decomposeEssentialMat
triangulatePoints

相关参考代码：

vector<Point2f> pts1;
vector<Point2f> pts2;
for ( int i = 0; i < ( int ) matches.size(); i++ ) {pts1.push_back(keypoints_1[matches[i].queryIdx].pt);pts2.push_back(keypoints_2[matches[i].trainIdx].pt);
}Mat matF = findFundamentalMat(pts1, pts2, CV_FM_8POINT);double cx = K.at<double>(0,2);
double cy = K.at<double>(1,2);
double fx = K.at<double>(0,0);
Mat matE = findEssentialMat(pts1, pts2, fx, Point2d(cx,cy));Mat matH = findHomography(pts1, pts2, RANSAC, 3);recoverPose(matE, pts1, pts2, R, t, fx, Point2d(cx,cy));

3D-2D: PnP

Perspective-n-Point is the problem of estimating the pose of a calibrated camera given a set of n 3D points in the world and their corresponding 2D projections in the image. [Wikipedia]

PnP(Perspective-n-Point) 是求解3D到2D点对运动的方法，求解PnP问题目前主要有直接线性变换（DLT）、P3P、EPnP、UPnP以及非线性优化方法。

在双目或RGB-D的视觉里程计中，可以直接使用PnP估计相机运动；而在单目视觉里程计中，必须先进行初始化，然后才能使用PnP。

在SLAM中，通常先使用 P3P或EPnP 等方法估计相机位姿，再构建最小二乘优化问题对估计值进行调整（BA）。

Bundle Adjustment

把 PnP问题构建成一个定义于李代数上的非线性最小二乘问题，求解最好的相机位姿。

定义残差（观测值-预测值）或重投影误差

$r(\xi) = u - K \exp({\xi}^{\wedge}) P$

构建最小二乘问题
${\xi}^* = \arg \min_\xi \frac{1}{2} \sum_{i=1}^{n} {\| r(\xi) \| }_2^2$

细节可参考应用: 基于李代数的视觉SLAM位姿优化

OpenCV 中相关函数：

solvePnP
Rodrigues

相关参考代码：

vector<KeyPoint> kpts_1, kpts_2;
vector<DMatch> matches;
find_feature_matches ( img_1, img_2, kpts_1, kpts_2, matches );vector<Point3f> pts_3d;
vector<Point2f> pts_2d;
for ( DMatch m : matches ) {int x1 = int(kpts_1[m.queryIdx].pt.x);int y1 = int(kpts_1[m.queryIdx].pt.y);ushort d = img_d.ptr<unsigned short>(y1)[x1];if (d == 0)   // bad depthcontinue;float dd = d / depth_scale;Point2d p1 = pixel2cam(kpts_1[m.queryIdx].pt, K);pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));pts_2d.push_back(kpts_2[m.trainIdx].pt);
}Mat om, t;
solvePnP ( pts_3d, pts_2d, K, Mat(), om, t, false, SOLVEPNP_EPNP );
Mat R;
cv::Rodrigues ( om, R ); // rotation vector to rotation matrixbundle_adjustment_3d2d ( pts_3d, pts_2d, K, R, t );

3D-3D: ICP

对于3D-3D的位姿估计问题可以用 ICP(Iterative Closest Point) 求解，其求解方式分为两种：

线性代数方式（主要是 SVD）
非线性优化方式（类似于BA）

线性代数方式

根据ICP问题，建立第 $i$ 对点的误差项

$e_i = P_i - (R \cdot {P'}_i + t)$

构建最小二乘问题，求使误差平方和达到极小的 $R, t$

$\min_{R,t} J = \frac{1}{2} \sum_{i=1}^{n} {\| e_i \|}_2^2$

对目标函数处理，最终为

$\min_{R,t} J = \frac{1}{2} \sum_{i=1}^{n} ( {\| P_i - P_c - R({P'}_i-{P'}_c) \|}^2 + {\| P_c - R{P'}_c - t \|}^2 )$

根据上式，可以先求解 $R$ ，再求解 $t$

计算两组点的质心 $P_c$ 和 ${P'}_c$
计算每个点的去质心坐标 $Q_i = P_i -P_c$ 和 ${Q'}_i = {P'}_i - {P'}_c$
定义矩阵 $\sum_{i=1}^{n} Q_i {Q'}_i^T$ ，再SVD分解 ${\Sigma} V^T$
当 $W$ 满秩时， $UV^T \quad$
计算 $P_c - R \cdot {P'}_c$

相关参考代码：

cv::Point3f p1, p2;
int N = pts1.size();
for (int i = 0; i < N; i++) {p1 += pts1[i];p2 += pts2[i];
}
p1 /= N;
p2 /= N;std::vector<cv::Point3f> q1(N), q2(N);
for (int i = 0; i < N; i++) {q1[i] = pts1[i] - p1;q2[i] = pts2[i] - p2;
}Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for (int i = 0; i < N; i++) {Eigen::Vector3d v3q1 = Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z);Eigen::Vector3d v3q2 = Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z);W += v3q1 * v3q2.transpose();
}double determinantW =W(0,0)*W(1,1)*W(2,2) + W(0,1)*W(1,2)*W(2,0) + W(0,2)*W(1,0)*W(2,1) -
(W(0,0)*W(1,2)*W(2,1) + W(0,1)*W(1,0)*W(2,2) + W(0,2)*W(1,1)*W(2,0));assert(determinantW>1e-8);// SVD on W
Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();R = U * (V.transpose());
t = Eigen::Vector3d(p1.x, p1.y, p1.z) - R * Eigen::Vector3d(p2.x, p2.y, p2.z);

Optical Flow

光流是一种描述像素随时间在图像之间运动的方法，计算部分像素的称为 稀疏光流，计算所有像素的称为 稠密光流。稀疏光流以 Lucas-Kanade光流 为代表，并可以在SLAM中用于跟踪特征点位置。

LK光流

灰度不变假设

$I (x + d x, y + d y, t + d t) = I (x, y, t)$

对左边一阶泰勒展开

$\frac{\partial I}{\partial x} dx + \frac{\partial I}{\partial y} dy + \frac{\partial I}{\partial t} dt$

则

$\frac{\partial I}{\partial x} dx + \frac{\partial I}{\partial y} dy + \frac{\partial I}{\partial t} dt = 0$

整理得

$\frac{\partial I}{\partial x} \frac{dx}{dt} + \frac{\partial I}{\partial y} \frac{dy}{dt} = - \frac{\partial I}{dt}$

简写为

$I_x u + I_y v = -I_t$

即

$\begin{bmatrix} I_x & I_y \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = -I_t$

在LK光流中，假设某个窗口（w x w）内的像素具有相同的运动

${\begin{bmatrix} I_x & I_y \end{bmatrix}}_k \begin{bmatrix} u \\ v \end{bmatrix} = -{I_t}_k, \quad k=1, \dots, w^2$

简写为

$\begin{bmatrix} u \\ v \end{bmatrix} = -b$

从而得到图像间的运动速度或者某块像素的位置。

分类

增量方式	Forward	Inverse
Additive	FAIA	IAFA
Compositional	FCIA	ICIA

Forward-Additive 光流:

$\min_{\Delta x_i, \Delta y_i} \sum_{W} {\| I_1(x_i,y_i) - I_2(x_i+\Delta x_i, y_i+\Delta y_i) \|}_2^2$

在迭代开始时，Gauss-Newton 的计算依赖于 $I_2$ 在 $x_i, y_i)$ 处的梯度信息。然而，角点提取算法仅保证了 $I_1(x_i,y_i)$ 处是角点(可以认为角度点存在明显梯度)，但对于 $I_2$ ，我们并没有办法假设 $I_2$ 在 $x_i,y_i)$ 处亦有梯度，从而 Gauss-Newton 并不一定成立。

反向的光流法(inverse) 则做了一个巧妙的技巧，即用 $I_1(x_i,y_i)$ 处的梯度，替换掉原本要计算的 $I_2(x_i+\Delta x_i, y_i+\Delta y_i)$ 的梯度。 $I_1(x_i,y_i)$ 处的梯度不随迭代改变，所以只需计算一次，就可以在后续的迭代中一直使用，节省了大量计算时间。

讨论

在光流中，关键点的坐标值通常是浮点数，但图像数据都是以整数作为下标的。在光流中，通常的优化值都在几个像素内变化，所以用浮点数的像素插值（双线性插值）。
光流法通常只能估计几个像素内的误差。如果初始估计不够好，或者图像运动太大，光流法就无法得到有效的估计(不像特征点匹配那样)。但是，使用图像金字塔，可以让光流对图像运动不那么敏感。
多层金字塔光流

OpenCV 中相关函数：

calcOpticalFlowPyrLK

相关参考代码：

for (int index = 0; index < count; index++) {color = colorImgs[index];depth = depthImgs[index];if (index == 0) {vector<cv::KeyPoint> kps;cv::Ptr<cv::FastFeatureDetector> detector =cv::FastFeatureDetector::create();detector->detect(color, kps);for (auto kp:kps)keypoints.push_back(kp.pt);last_color = color;continue;}if (color.data == nullptr || depth.data == nullptr)continue;vector<cv::Point2f> next_keypoints;vector<cv::Point2f> prev_keypoints;for (auto kp:keypoints)prev_keypoints.push_back(kp);vector<unsigned char> status;vector<float> error;cv::calcOpticalFlowPyrLK(last_color, color, prev_keypoints, next_keypoints, status, error);int i = 0;for (auto iter = keypoints.begin(); iter != keypoints.end(); i++) {if (status[i] == 0) {iter = keypoints.erase(iter);continue;}* iter = next_keypoints[i];iter++;}last_color = color;
}

Direct Method

根据使用像素的数量，直接法分为以下三种

稀疏直接法：使用稀疏关键点，不计算描述子
半稠密直接法：只使用带有梯度的像素点，舍弃像素梯度不明显的地方
稠密直接法：使用所有像素

利用直接法计算相机位姿，建立优化问题时，最小化的是 光度误差（Photometric Error）

$r(\xi) = I_1(p) - I_2(p') = I_1(p) - I_2( K \exp({\xi}^{\wedge}) P )$

构建最小二乘问题
${\xi}^* = \arg \min_\xi \frac{1}{2} \sum_{i=1}^{n} {\| r(\xi) \| }_2^2$

更具体地，稀疏直接法

${\xi}^* = \arg \min_\xi \frac{1}{N} \sum_{i=1}^N \sum_{W_i} {\| I_1(p_i) - I_2 (\pi(\exp({\xi}^{\wedge}) \pi_{-1}(p_i))) \|}_2^2$

其雅克比矩阵的计算，可参见视觉SLAM位姿优化时误差函数雅克比矩阵的计算

相关参考代码：

bool pose_estimation_direct(const vector<Measurement>& measurements,cv::Mat* gray, Eigen::Matrix3f& K, Eigen::Isometry3d& Tcw) {typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 1>> DirectBlock;DirectBlock::LinearSolverType * linearSolver =new g2o::LinearSolverDense<DirectBlock::PoseMatrixType>();DirectBlock * solver_ptr = new DirectBlock(linearSolver);g2o::OptimizationAlgorithmLevenberg * solver =new g2o::OptimizationAlgorithmLevenberg(solver_ptr);g2o::SparseOptimizer optimizer;optimizer.setAlgorithm(solver);optimizer.setVerbose(true);g2o::VertexSE3Expmap * pose = new g2o::VertexSE3Expmap();pose->setEstimate(g2o::SE3Quat(Tcw.rotation(), Tcw.translation()));pose->setId(0);optimizer.addVertex(pose);int id = 1;for (Measurement m: measurements) {EdgeSE3ProjectDirect * edge =new EdgeSE3ProjectDirect(m.pos_world, K(0, 0), K(1, 1), K(0, 2), K(1, 2), gray);edge->setVertex(0, pose);edge->setMeasurement(m.grayscale);edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity());edge->setId(id++);optimizer.addEdge(edge);}optimizer.initializeOptimization();optimizer.optimize(30);Tcw = pose->estimate();
}