本文主要是介绍[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 0.子序列 vs 子数组
- 1.最长递增子序列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.摆动序列
- 1.题目链接
- 2.题目链接
- 3.代码实现
0.子序列 vs 子数组
- 子序列:
- 相对顺序是跟源字符串/数组是一致的
- 但是元素和元素之间,在源字符串/数组中可以是不连续的
- 一般时间复杂度: O ( 2 n ) O(2^n) O(2n)
- 子数组:
- 在源字符串/数组中挑出来,必须是连续的
- 子串与子数组是一个意思
- 一般时间复杂度: O ( N 2 ) O(N^2) O(N2)
- 在源字符串/数组中挑出来,必须是连续的
- 子序列其实相当于包含了子数组
- 子序列问题经典解法:两层循环
1.最长递增子序列
1.题目链接
- 最长递增子序列
2.算法原理详解
- 注意:本题思考方式非常有标志性
- 思路:
-
确定状态表示 ->
dp[i]的含义- 以
i位置元素为结尾的所有子序列中,最长递增子序列的长度
- 以
-
推导状态转移方程
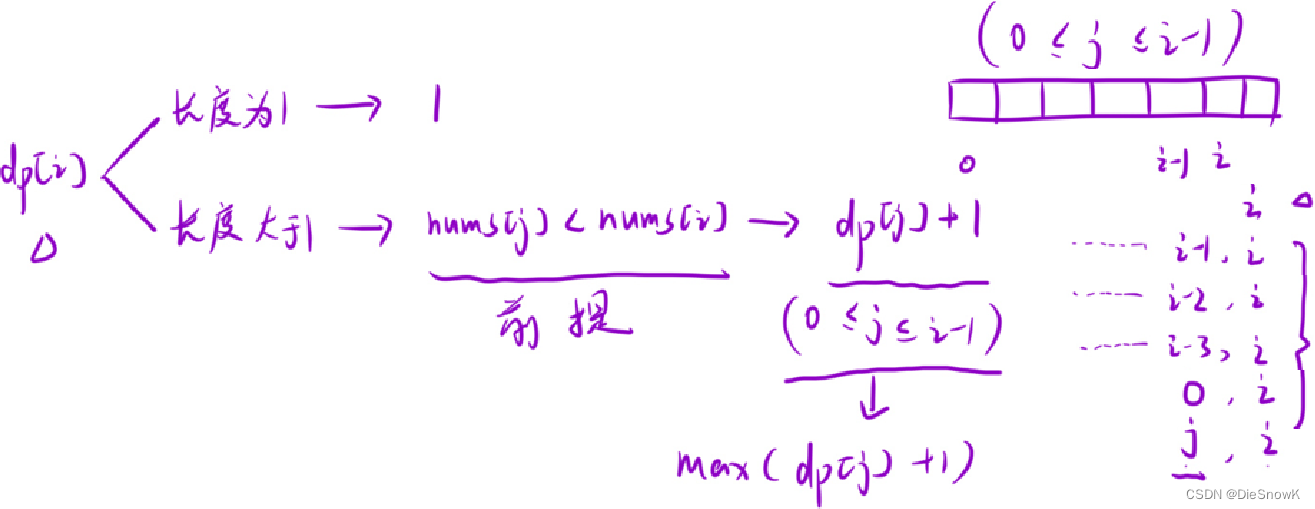
-
初始化:
vector<int> dp(n, 1) -
确定填表顺序:从左往右
-
确定返回值:整个
dp表里的最大值
-
3.代码实现
int lengthOfLIS(vector<int>& nums)
{int n = nums.size();vector<int> dp(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]){dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;
}
2.摆动序列
1.题目链接
- 摆动序列
2.题目链接
- 思路:
-
确定状态表示 ->
dp[i]的含义- 以
i位置元素为结尾的所有子序列中,最长的摆动序列的长度 - 本题状态标识还可以继续划分
f[i]:以i位置元素为结尾的所有子序列中,最后一个位置呈现“上升”趋势的最长的摆动序列的长度g[i]:以i位置元素为结尾的所有子序列中,最后一个位置呈现“下降”趋势的最长的摆动序列的长度
- 以
-
推导状态转移方程
- 令
j为i前面的任一一个数
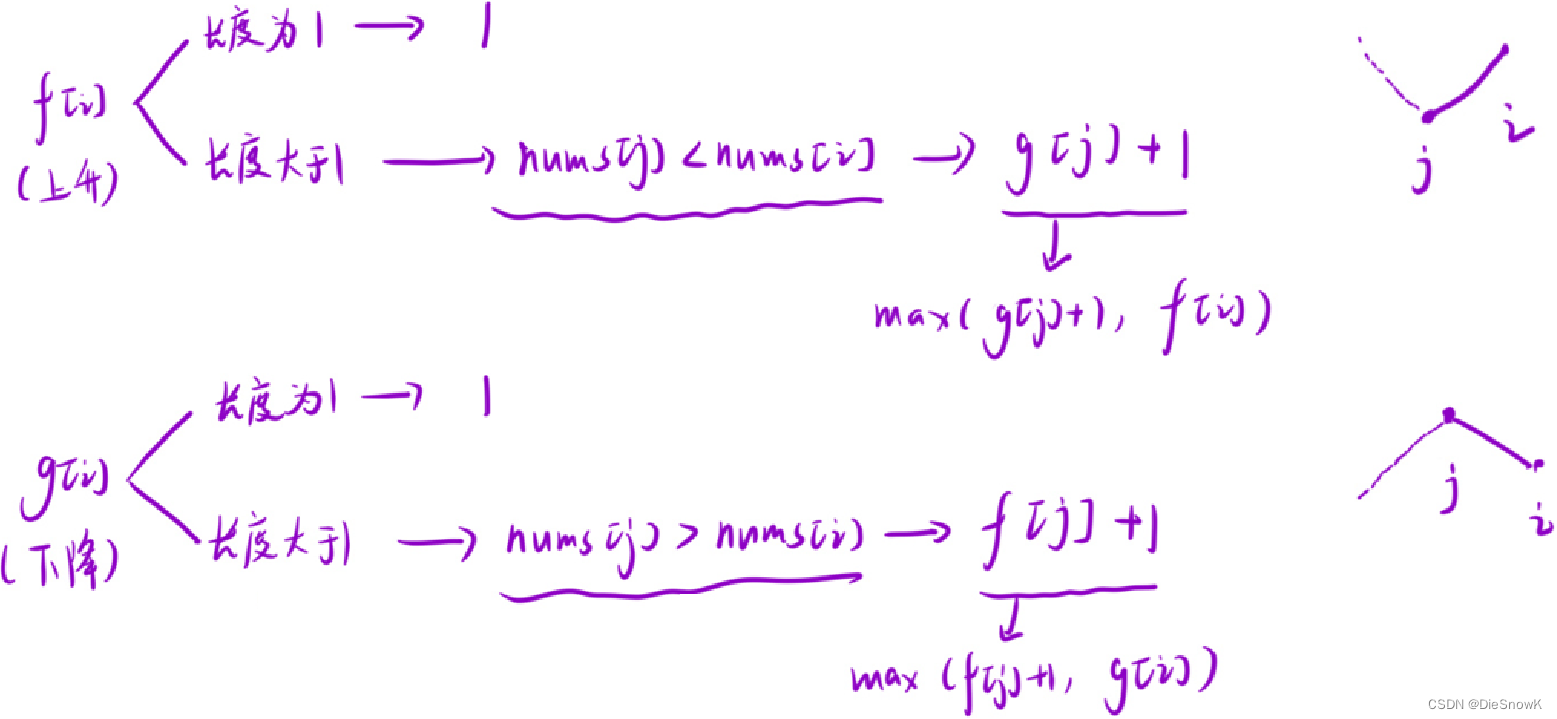
- 令
-
初始化:
vector<int> f(n, 1), g(n, 1) -
确定填表顺序:从左往右,两个表一起填
-
确定返回值:两个
dp表里的最大值
-
3.代码实现
int wiggleMaxLength(vector<int>& nums)
{int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]){f[i] = max(f[i], g[j] + 1);}else if(nums[j] > nums[i]){g[i] = max(g[i], f[j] + 1);}}ret = max(ret, max(f[i], g[i]));}return ret;
}
这篇关于[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







