本文主要是介绍水质预测模型精度评估实例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
研究背景
随着水资源管理需求的日益增长,水质预测模型的精准度成为了评估其有效性的关键因素。本文旨在通过实证研究,探讨自建水质预测模型的实际应用效能,通过与真实监测数据的比对,揭示模型预测精度的真实情况。
数据基础情况
数据来源:自研水质模型预测结果
时间范围:2023 年全年
指标:高锰酸盐指数、总磷、氨氮、氟化物
模型简介
本研究采用基于一维水质的机理模型,通过实时监测数据动态调整降解系数与污染物迁移速度,实现了单次对高锰酸盐指数、总磷、氨氮、氟化物长达20天以上的高适应性预测,尤其擅长捕捉水质突变事件。
当前预测界面
曲线图展示当前最新的预测结果。下部展示预测结果是否超标,峰值及超标时间范围,预测月均值与实际累计月均值。
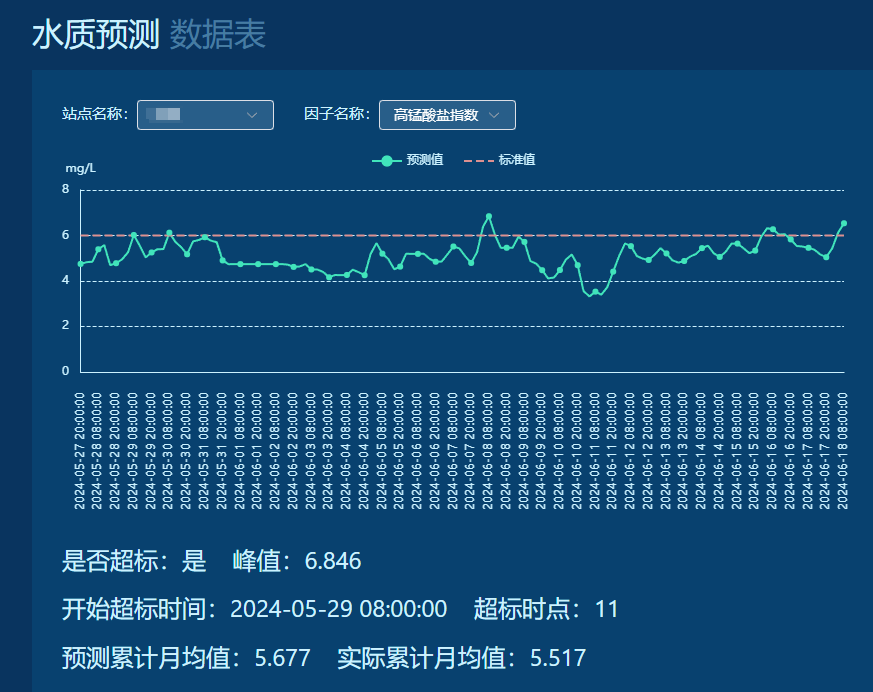
模型评价界面
可以查询历史预测区间的预测结果对比。下部为模型评价,通过多元统计指标(如MAPE、RMSE)深入剖析模型性能,特别是通过准确率区间分布图,多维度验证了模型的稳定性和可靠性。
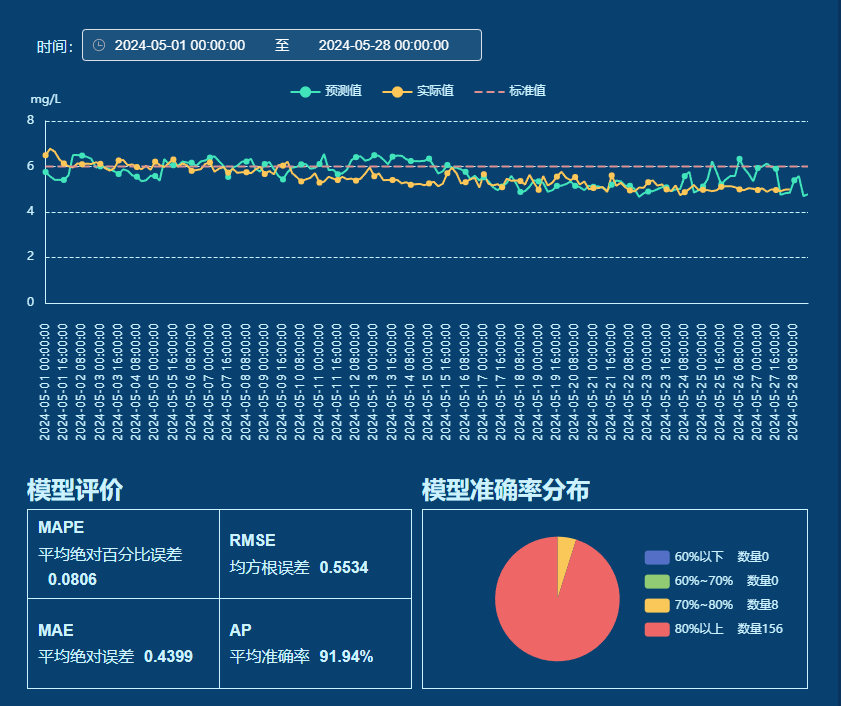
模型精度评价方法
为了评估模型的准确率,本文采用比较直观的“预测误差率”来表达,用于评估预测值与真实值之间的接近程度。
A = 1 − ∣ Y − Y ^ ∣ Y \text{A} = 1 - \frac{|Y - \hat{Y}|}{Y} A=1−Y∣Y−Y^∣
A 表示相对准确性,𝑌 是观测到的真实值(或准确值),而 Y^ 是模型预测的值。这个公式量化了预测误差相对于真实值的比例,其逆值给出了预测相对于实际观察值的接近程度,可以视为一种衡量预测准确性的度量,这种表达通常被称为相对误差的倒数或者归一化绝对误差。
理论情况下,模型每天至少运行一次,预测因子包括高锰酸盐指数、总磷、氨氮、氟化物,每次预测不少于 7 天,模型评价方法是每个因子,每次所有预测结果,依次与监测指标进行比对,单个指标每次每个值得预测准确率计为 A。
A ˉ = 1 N ∑ i = 1 N A i \bar{{A}} = \frac{1}{N} \sum_{i=1}^{N} A_i Aˉ=N1i=1∑NAi
这段公式表示求所有单次单个因子所有预测值的算术平均,其中 N 是预测值的数量。
用这种方法观察一年每次预测准确率的变化。
Python 代码实现
创建了一个 WaterQualityPredictor 类,该类封装与数据库交互、数据处理、预测数据获取、监测数据获取、准确率计算以及绘图等操作。
import pandas as pd
import matplotlib.pyplot as plt
import pymysql
from datetime import datetime
from sklearn.metrics import mean_absolute_error
class WaterQualityPredictor:def __init__(self, db_config):self.db_config = db_configself.conn = self._connect_db() def _connect_db(self):"""连接数据库"""conn = pymysql.connect(**self.db_config)return conndef fetch_model_data(self, sql):"""从数据库获取模型数据"""df = pd.read_sql(sql, self.conn)return self._process_data(df) @staticmethoddef _process_data(df):"""处理数据,包括时间格式转换和数值处理"""df["create_time"] = pd.to_datetime(df["create_time"])df["start_time"] = pd.to_datetime(df["start_time"])df["date_time"] = pd.to_datetime(df["date_time"])for col in ["CODmn", "NH3", "TP", "F"]:df[col] = df[col].astype(float).round(3)return dfdef get_prediction_dataset(self, factor, create_time, prediction_days=7):"""根据因子和创建时间获取预测数据集"""subset = self.model_data[(self.model_data["create_time"] == create_time) & (self.model_data[factor].notnull())].iloc[:6*prediction_days]subset = subset[["date_time", factor]].set_index("date_time").reset_index()return subsetdef fetch_monitor_data(self, begin_time, end_time, station, period):"""获取监测数据"""# 这里省略具体的请求逻辑,pass def calculate_accuracy(self, prediction_df, monitor_df, factor):"""计算准确率"""concatenated_data = pd.merge(prediction_df, monitor_df, on="date_time", suffixes=('', '_y'))concatenated_data['Accuracy'] = 1 - (abs(concatenated_data[factor] - concatenated_data[factor+'_y']) / concatenated_data[factor])concatenated_data['Accuracy'] = concatenated_data['Accuracy'] * 100average_accuracy = concatenated_data['Accuracy'].mean()return round(average_accuracy, 4)def plot_comparison(self, concatenated_data, factor):"""绘制预测值与监测值对比图"""if concatenated_data['date_time'].equals(concatenated_data['date_time_y']):plt.figure(figsize=(10, 6))plt.plot(concatenated_data['date_time'], concatenated_data[factor], label='Prediction', marker='o')plt.plot(concatenated_data['date_time_y'], concatenated_data[factor+'_y'], label='Monitor', marker='x')plt.xlabel('Date Time')plt.ylabel(factor + ' Value')plt.title(f'Comparison of {factor} Prediction and Monitor Values')plt.xticks(rotation=45)plt.legend()plt.show()else:print("date_time and date_time_y are not aligned")def run_analysis(self, factor, create_time, station, period, prediction_days=7):"""执行整个分析流程"""self.model_data = self.fetch_model_data("SELECT * FROM mechanism")prediction_df = self.get_prediction_dataset(factor, create_time, prediction_days)monitor_df = self.fetch_monitor_data(prediction_df["date_time"].min(), prediction_df["date_time"].max(), station, period)accuracy = self.calculate_accuracy(prediction_df, monitor_df, factor)print(f"Average Accuracy: {accuracy}%")self.plot_comparison(pd.concat([prediction_df, monitor_df], axis=1), factor) if __name__ == "__main__":db_config = {"host": "","port": ,"user": "","password": "","db": "","charset": ""}predictor = WaterQualityPredictor(db_config)predictor.run_analysis("factor", datetime.now() - timedelta(days=7), "station", "h4")
实现任意预测时间的单词预测结果对比。
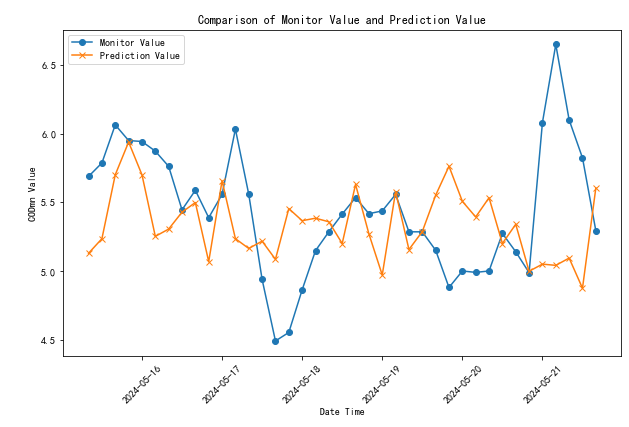
折线图分析准确率变化
循环计算单词预测结果,取 2023 年整个时间段,四个指标准确率变化分别绘图。
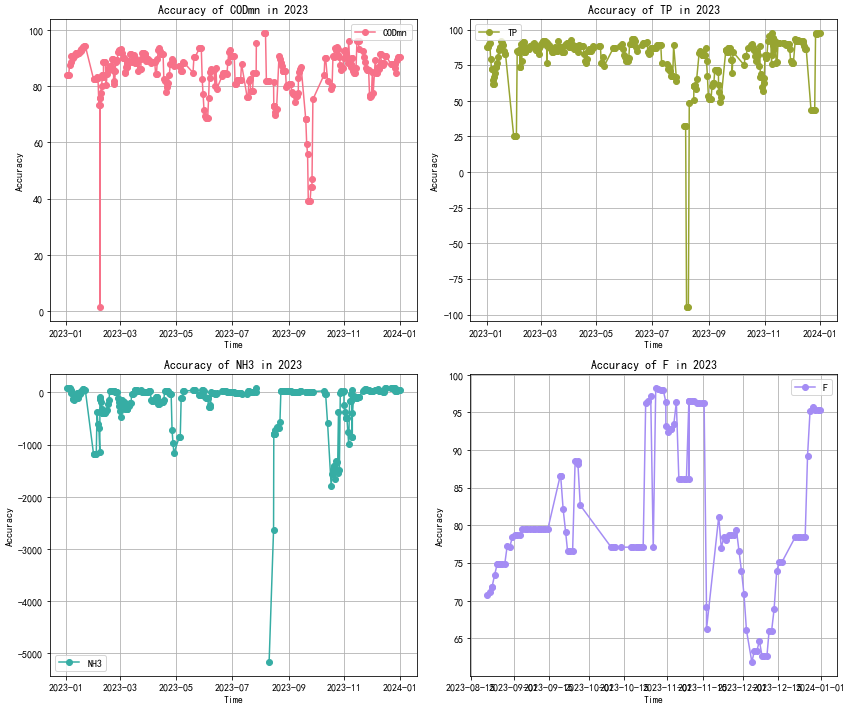
注:部分预测异常时段,存在站点运行问题,为展示真实预测情况,未对齐进行剔除。从预测异常的频次看出,异常频率并不高。
饼图分析准确率占比
为了更直观的分析预测准确率的分布,对四个因子准确率的分布划分为(小于40, 40~60, 60~80, 80~100)四个区间,分别作图如下。
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
def prepare_data_for_piechart(df, column):bins = [-np.inf, 40, 60, 80, 100]labels = ['<40%', '40%-60%', '60%-80%', '80%-100%']# 使用cut函数将数据切分为区间,并计算每个区间内数据点的数量intervals = pd.cut(df[column], bins=bins, labels=labels, include_lowest=True)# 计算每个区间的频率frequencies = intervals.value_counts(normalize=True) * 100return frequencies
columns_to_analyze = df_2023.columns.tolist()
fig, axs = plt.subplots(2, 2, figsize=(12, 8), facecolor='white')
axs = axs.ravel() # 将2x2的数组展平以便循环
for i, column in enumerate(columns_to_analyze):if i < len(axs): # 确保不会超出子图的范围frequencies = prepare_data_for_piechart(df_2023, column)axs[i].pie(frequencies, labels=frequencies.index, autopct='%1.1f%%')axs[i].set_title(f'{column} Precision Distribution')axs[i].axis('equal') # 确保饼图是圆形
# 隐藏未使用的子图
for j in range(i+1, len(axs)):fig.delaxes(axs[j])
plt.tight_layout()
plt.show()
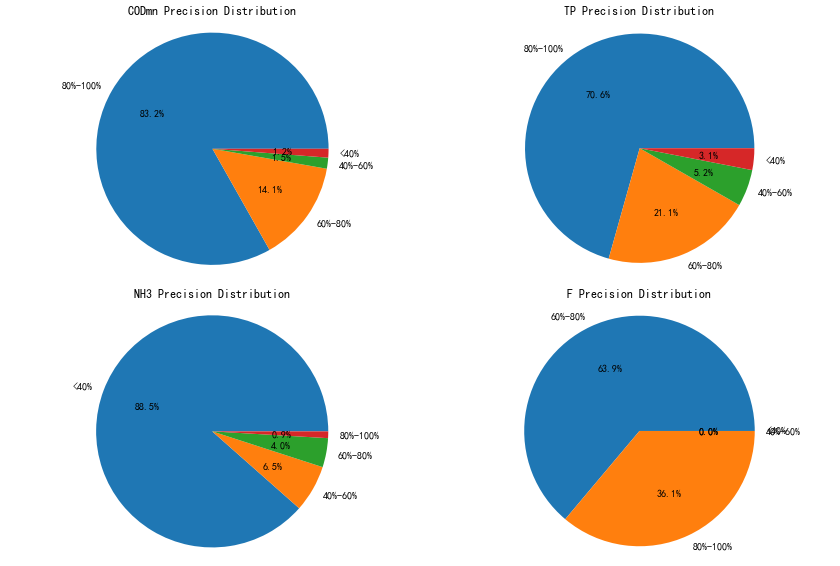
上图表明,高锰酸盐指数准确率超过 60%的比例占比 95.4%,总磷准确率准确率超过 60%的比例 91.7%。详细指标可见下表。
| 年平均准确率 | 预测天数 | >80% | 80~ 60% | |
|---|---|---|---|---|
| 高锰酸盐指数 | 84.78 | 327 | 83.2 | 14.1 |
| 总磷 | 79.52 | 327 | 70.6 | 21.1 |
| 氨氮 | -186 | 321 | 0.9 | 4 |
| 氟化物 | 81.27 | 119 | 36.1 | 63.95 |
| 注:受站点运行情况影响,部分时段无数据。 |
直方图分析准确率分布
直方图(Histogram)是一个更好的可视化选择,因为它能清晰地展示每个准确率区间内的数据点数量,非常适合观察数据分布特征,如中心趋势、偏斜程度及异常值等。
import matplotlib.pyplot as plt
bin_width = 10
bins = list(range(0, 110, bin_width)) + [100] # 包含100%的边界
# 创建一个2x2的子图网格
fig, axs = plt.subplots(2, 2, figsize=(12, 10))
# 遍历每个因子,并绘制其准确率的直方图
for i, column in enumerate(df_2023.columns):row = i // 2col = i % 2# 绘制直方图axs[row, col].hist(df_2023[column], bins=bins, edgecolor='black', alpha=0.7)axs[row, col].set_title(f'{column} Accuracy Distribution')axs[row, col].set_xlabel('Accuracy (%)')axs[row, col].set_ylabel('Frequency')
# 如果因子少于4个,隐藏多余的子图
for ax in axs.flat[len(df_2023.columns):]:ax.axis('off')
# 紧凑布局
plt.tight_layout()
plt.show()
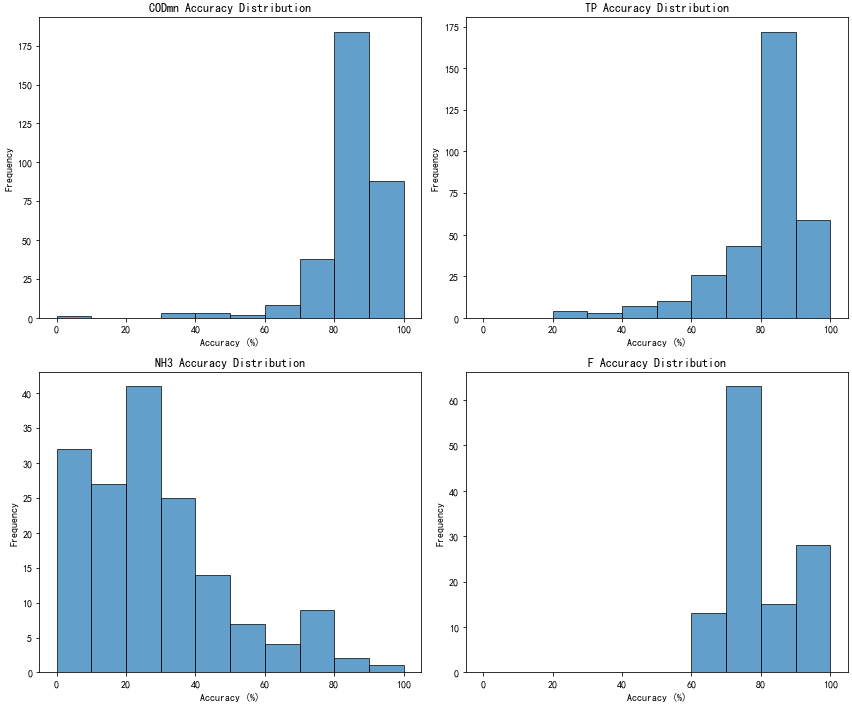
直方图能清晰的看出高锰酸盐指数、总磷预测准确率更好,且分布更集中。
本模型氨氮预测准确率低的原因是:该目标站点氨氮指标长期较低。月均值波动在 0~0.2 之间,小时值可能长期处于 0~0.1 之间,即使较小的波动,准确率的值波动也很大。同时氨氮指标该站点与上游站点的关系不密切,只有较大的污染传递才能引起轻微升高。
经过长期观察,氨氮并非该站点的重点污染指标。
结论
- 机理模型在某站点高锰酸盐指数、总磷、氟化物等指标 2023 年的预测均有较好的表现。以准确率(归一化绝对误差的逆)评价,累计分别为 84.78%、79.52%、81.27%。
- 由于氨氮值较低,且与上游站点变化较弱,对于氨氮指标的预测准确率不高。也因为氨氮值较低并非重点关注对象,若要考虑提高预测精度,可选择大数据模型,如 LSTM、prophet 等。
- 准确率(归一化绝对误差的逆)并不是水质模型精度评价的必选指标,只是因为其较为通俗易懂,而受用户认可,仍需注意其具有一定的局限性,作为一个模型评价的参考指标即可,不宜过分求高,水质模型是否准确,应考虑其预测水质变化的能力,水质影响(峰值、污染持续时间)等,是否能够知道业务需要,才是水质模型最重要的指标。
综上所述,本研究构建的机理模型在多数水质指标预测上展现了良好的效果,尤其在高锰酸盐指数、总磷和氟化物的预测上取得了显著成绩。然而,氨氮预测的挑战凸显了模型对低浓度污染物处理能力的局限,后续将结合先进的机器学习技术以增强特定条件下的预测能力。水质模型的终极目标不仅是追求高精度数值,更重要的是能否有效指导水环境管理和应对策略,确保模型服务于实际的环境治理需求。
以上就是实际机理模型的应用精度分析,如果对你有启发,请点赞关注,如果有不对的地方请帮忙指正,水质预测是很小众的领域,希望得到同行的支持和指导。
微信公众号:环境猫er
这篇关于水质预测模型精度评估实例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





