本文主要是介绍【机器学习300问】103、简单的经典卷积神经网络结构设计成什么样?以LeNet-5为例说明。,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一个简单的经典CNN网络结构由:输入层、卷积层、池化层、全连接层和输出层,这五种神经网络层结构组成。它最最经典的实例是LeNet-5,它最早被设计用于手写数字识别任务,包含两个卷积层、两个池化层、几个全连接层,以及最后的输出层。
一、先用文字介绍一下这五层分别在做什么
(1)输入层
输入通常是经过预处理的图像数据,例如,将图像调整到特定尺寸(如32x32x3)并进行归一化,使得像素值范围在0到1之间,或者被标准化为均值为0,标准差为1的形式。
(2)卷积层
卷积层是CNN的关键组成部分,又可以拆分成下面4分部分逐一理解:
- 卷积核(Filter/Kernels):每个卷积层包含多个可学习的滤波器(或称为卷积核),这些滤波器在输入图像上滑动,执行卷积操作(相乘后求和),从而检测图像中的特定特征,如边缘、线条、纹理等。
- 步长(Stride):滤波器在图像上移动的步长,决定了输出特征图的空间分辨率。
- 填充(Padding):通常为了保持输出特征图的尺寸或避免边界信息的丢失,会在图像边缘添加零(Zero Padding)。
- 激活函数:如ReLU(Rectified Linear Unit)用于增加网络的非线性。
(3)池化层
池化层的负责减少特征图的空间尺寸,降低计算复杂度,同时保持最重要的特征。最常见的池化类型是最大池化(Max Pooling),它在每个池化区域取最大值作为输出。池化同样有步长和大小的参数,比如常用的2x2大小,步长为2。
(4)全连接层
在一系列卷积和池化层之后,特征图会被展平(Flatten)成一维向量,然后传递给全连接层。全连接层负责将学到的特征映射到分类标签或其他输出形式。全连接层是传统神经网络的一部分,常用于模型的最终分类或回归任务。
(5)输出层
对于分类任务,输出层通常使用Softmax激活函数,将神经元的输出转换为概率分布,表示每个类别的预测概率。输出层的神经元数量等于分类任务的类别总数。
二、再用可视化加深对经典CNN结构的理解
(1)经典CNN结构
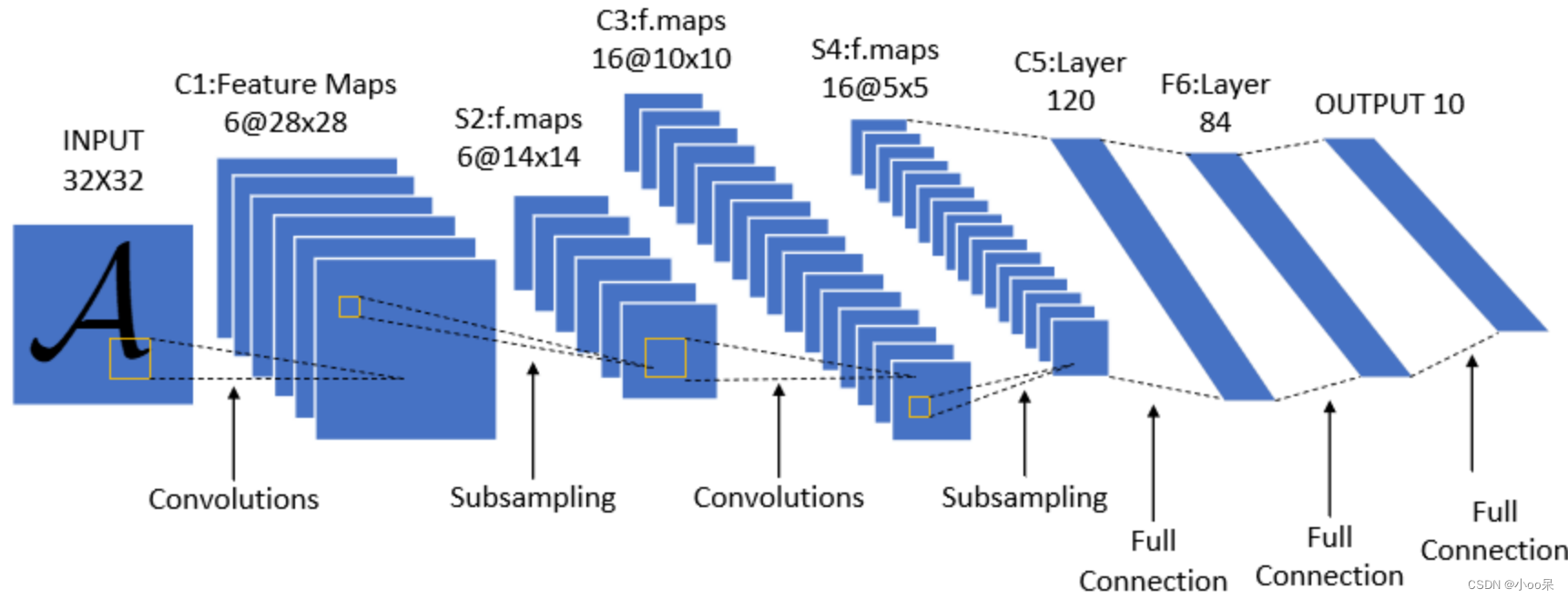
CNN有个特点,5个层组成(输入层、卷积层、池化层、全连接层和输出层),在神经网络的隐藏层部分,卷积层和池化层交替出现,最后跟上几个全连接层再跟输出层。
重复的卷积层与池化层的组合目的是为了学习更深层次、更复杂的特征,每次这样的组合都会使网络能够捕捉到更高层次的抽象特征,如从边缘逐步过渡到形状、纹理乃至对象的部分和整体。
(2)这样的网络结构设计会出现一种现象
经过这样的网络结构后,图像的尺寸会减小,图像的通道数
会增大。 这种变化反映了网络从原始像素数据中提取并逐步构建更高级、更抽象特征的过程。对此现象稍作解释:
① 图像尺寸减小:
- 卷积层:卷积层本身不一定会减少图像尺寸,但可以通过设置合适的填充(padding)和步长(stride)来控制输出尺寸。无填充且步长大于1的卷积会缩小输出尺寸。
- 池化层:池化层的主要作用之一就是减少空间维度(高度和宽度),通常在每个维度上减半,从而显著减小图像尺寸,同时保持最重要的特征。
② 通道数增大:
- 卷积层:每个卷积层通过不同的卷积核学习不同的特征,每个卷积核会产生一个新的通道。因此,卷积层后的通道数通常会增加,具体增加的数量等于该层中滤波器(卷积核)的数量。
- 池化层:池化操作不会改变通道数,它只影响空间维度。
- 全连接层:进入全连接层之前,所有之前的层(包括卷积层和池化层)的输出会被“展平”成一维向量,此时不再讨论“通道”这个概念,而是关注于神经元的总数。
这篇关于【机器学习300问】103、简单的经典卷积神经网络结构设计成什么样?以LeNet-5为例说明。的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







