本文主要是介绍DINO结构中的exponential moving average (ema)和stop-gradient (sg),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
DINO思路介绍
在 DINO 中,教师和学生网络分别预测一个一维的嵌入。为了训练学生模型,我们需要选取一个损失函数,不断地让学生的输出向教师的输出靠近。softmax 结合交叉熵损失函数是一种常用的做法,来让学生模型的输出与教师模型的输出匹配。具体地,通过 softmax 函数把教师和学生的嵌入向量尺度压缩到 0 到 1 之间,并计算两个向量的交叉熵损失。这样,在训练过程中,学生模型可以通过模仿教师模型的输出来学习更好的特征表示,从而提高模型的性能和泛化能力。当然,这也可以看作是一个分类问题,以便网络可以从局部视图中学习更有意义的全局表示。
论文对图片中DINO结构的解释如下
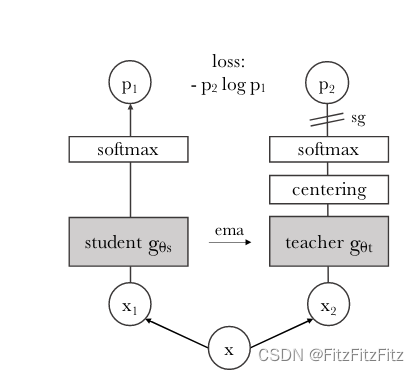
我们用一个简单的视角对 (x1, x2) 来说明DINO。在该模型中,输入图像经过两种不同的随机变换后分别传递给学生网络和教师网络。两个网络具有相同的架构但参数不同。教师网络的输出以批次的均值进行中心化。每个网络输出一个K 维的特征,并通过特征维度上的温度 softmax进行归一化。然后通过交叉熵损失函数来测量它们的相似性。我们在教师网络上应用一个停止梯度(stop-gradient,sg)操作,以仅通过学生网络传播梯度。教师网络的参数通过学生网络参数的指数移动平均(ema)来更新。
核心特点
无标签自蒸馏: 不需要人工标注的数据,通过模型自身的知识传递来进行训练。
双视角 (x1, x2): 输入图像经过两种不同的随机变换,生成两种视角,以增加数据的多样性和模型的鲁棒性。
学生网络和教师网络: 两个网络结构相同,但参数不同。学生网络用于训练,教师网络提供稳定的指导信号。
教师网络输出中心化: 教师网络的输出在批次内进行中心化处理,以消除偏差并稳定训练过程。
温度 Softmax 归一化: 网络输出通过温度 Softmax 进行归一化,控制特征向量的平滑度,防止梯度消失或爆炸。
相似性度量: 通过交叉熵损失函数测量学生网络和教师网络输出之间的相似性,鼓励学生网络学习到与教师网络相似的表示。
停止梯度操作(SG): 在教师网络上应用停止梯度操作,确保梯度只通过学生网络进行反向传播,避免教师网络影响梯度更新。
指数移动平均更新(EMA): 教师网络的参数通过学生网络参数的指数移动平均进行更新,确保教师网络的参数更加平滑和稳定,从而提供可靠的指导信号。
再总结一下:在两个完全一样的教师和学生网络(ViT/CNN 均可)中
- 教师网络通过 centering 和 sharpening 正则化避免训练崩塌。
-
- Centering:教师模型的输出也经过 EMA 操作,从原始激活值中减去一个平均值。
-
- Sharpening:在 Softmax 中加入一个 temperature 参数,强制让概率分布更加尖锐。
- 两个网络的输出都通过 Softmax 层归一化处理。
- 通过交叉熵损失计算损失。
-
- 学生网络通过 SGD 更新参数,并通过 EMA 更新教师网络参数,教师网络的参数因为sg不会自己动**。
问题一:centering中使用的EMA(Exponential Moving Average)是什么东西,指数是怎么被体现的
在 DINO 中,教师网络的参数通过学生网络参数的指数移动平均(Exponential Moving Average, EMA)进行更新。以下是 EMA 操作的详细解释:
1. 定义
EMA 是一种用于平滑时间序列数据的技术,它通过对新数据赋予较高权重,同时对旧数据赋予较低权重,从而平滑数据变化。具体来说,EMA 的计算公式为:
θ t teacher = α θ t student + ( 1 − α ) θ t − 1 teacher \theta_t^{\text{teacher}} = \alpha \theta_t^{\text{student}} + (1 - \alpha) \theta_{t-1}^{\text{teacher}} θtteacher=αθtstudent+(1−α)θt−1teacher
其中:
- θ t teacher \theta_t^{\text{teacher}} θtteacher 是第 t t t 次更新后的教师网络参数。
- θ t student \theta_t^{\text{student}} θtstudent 是第 t t t 次学生网络的参数。
- α \alpha α 是平滑系数,介于 0 和 1 之间,通常取一个较小的值(例如 0.99 或 0.999)。
- θ t − 1 teacher \theta_{t-1}^{\text{teacher}} θt−1teacher 是第 t − 1 t-1 t−1 次更新后的教师网络参数。
2. 指数的体现
EMA 操作中的“指数”体现在计算过程中旧数据的权重以指数形式递减。具体地,如果我们展开几次 EMA 的更新,可以看到:
θ t teacher = α θ t student + α ( 1 − α ) θ t − 1 student + α ( 1 − α ) 2 θ t − 2 student + ⋯ \theta_t^{\text{teacher}} = \alpha \theta_t^{\text{student}} + \alpha(1 - \alpha) \theta_{t-1}^{\text{student}} + \alpha(1 - \alpha)^2 \theta_{t-2}^{\text{student}} + \cdots θtteacher=αθtstudent+α(1−α)θt−1student+α(1−α)2θt−2student+⋯
这表明旧数据的权重以 ( (1 - \alpha)^k ) 的形式递减,其中 ( k ) 是时间步长。因此,最近的数据对当前参数的影响最大,而更早的数据影响则逐渐减小,以指数形式衰减。
3. 核心思想
EMA 操作的核心思想是使教师网络参数逐步融合学生网络的最新知识,同时保留一部分历史信息。这使得教师网络参数更新更加平滑,避免剧烈波动,从而提供稳定的指导信号。
4. 优点
- 稳定性:通过 EMA,教师网络参数的变化更加平滑,减小了训练过程中的不稳定性。
- 延迟效应:EMA 赋予新数据较高权重,能够快速反映学生网络的最新学习成果,同时历史信息的保留可以防止模型过拟合于噪声数据。
- 无梯度反传:在 DINO 中,教师网络的参数更新不需要反向传播梯度,EMA 操作直接基于学生网络参数进行更新,这简化了计算。
5. 在 DINO 中的应用
在 DINO 的训练过程中,教师网络的参数不参与反向传播,而是通过 EMA 操作根据学生网络的参数进行更新。这确保了教师网络能够稳定地指导学生网络学习,同时防止了学生网络的梯度直接影响教师网络。
途中右上角有个sg,这个停止梯度操作又是什么
停止梯度操作 (Stop-Gradient)
在 DINO 中,我们在教师网络上应用了停止梯度(stop-gradient, sg)操作,使得梯度只通过学生网络进行传播。具体来说,停止梯度操作的目的是阻止梯度在反向传播时更新教师网络的参数,而仅更新学生网络的参数。
定义
停止梯度操作是一种在反向传播过程中冻结部分网络参数的技术。通过这种操作,某些部分的网络参数不会更新,以保持其值不变。
作用与优点
- 保持教师网络的稳定性:通过停止梯度操作,教师网络的参数在训练过程中保持不变,这有助于提供稳定的指导信号。
- 防止梯度泄漏:停止梯度操作可以防止梯度从学生网络泄漏到教师网络,从而确保梯度仅用于更新学生网络的参数。
- 增强训练效果:这种操作确保学生网络在训练过程中受到稳定的指导信号,促进其更有效地学习。
在 DINO 中的应用
在 DINO 的训练过程中,教师网络的参数通过指数移动平均(EMA)从学生网络的参数中更新,但不参与反向传播。具体来说:
- 我们对教师网络应用停止梯度操作,使得梯度不通过教师网络进行传播。
- 教师网络的参数更新通过 EMA 操作,从学生网络的参数中获得。
停止梯度操作 (Stop-Gradient)
在 DINO 中,我们在教师网络上应用了停止梯度(stop-gradient, sg)操作,使得梯度只通过学生网络进行传播。具体来说,停止梯度操作的目的是阻止梯度在反向传播时更新教师网络的参数,而仅更新学生网络的参数。
定义
停止梯度操作是一种在反向传播过程中冻结部分网络参数的技术。通过这种操作,某些部分的网络参数不会更新,以保持其值不变。
作用与优点
- 保持教师网络的稳定性:通过停止梯度操作,教师网络的参数在训练过程中保持不变,这有助于提供稳定的指导信号。
- 防止梯度泄漏:停止梯度操作可以防止梯度从学生网络泄漏到教师网络,从而确保梯度仅用于更新学生网络的参数。
- 增强训练效果:这种操作确保学生网络在训练过程中受到稳定的指导信号,促进其更有效地学习。
在 DINO 中的应用
在 DINO 的训练过程中,教师网络的参数通过指数移动平均(EMA)从学生网络的参数中更新,但不参与反向传播。具体来说:
- 我们对教师网络应用停止梯度操作,使得梯度不通过教师网络进行传播。
- 教师网络的参数更新通过 EMA 操作,从学生网络的参数中获得。
这篇关于DINO结构中的exponential moving average (ema)和stop-gradient (sg)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






