强化学习，第 2 部分：政策评估和改进

本文主要是介绍强化学习，第 2 部分：政策评估和改进，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、介绍

二、关于此文章

三、求解贝尔曼方程

四、策略评估

4.1 更新变体

4.2 例描述

五、策略改进

5.1 V函数描述

5.2 政策改进定理

六、策略迭代

七、值迭代

7.1 算法描述

7.2 异步值迭代

八、广义策略迭代

九、结论

一、介绍

R强化学习是机器学习中的一个领域，它引入了必须在复杂环境中学习最优策略的智能体的概念。智能体从其行为中学习，这些行为在给定环境状态的情况下产生奖励。强化学习是一个困难的话题，与机器学习的其他领域有很大不同。这就是为什么只有当给定的问题无法解决时才应该使用它。

强化学习令人难以置信的灵活性在于，可以使用相同的算法使智能体适应完全不同的、未知的和复杂的条件。

注意。为了充分理解本文中包含的思想，强烈建议您熟悉本系列文章第一部分中介绍的强化学习的主要概念。

二、关于此文章

在第 1 部分中，我们介绍了强化学习的主要概念：框架、策略和价值函数。递归建立值函数关系的贝尔曼方程是现代算法的支柱。在本文中，我们将通过学习如何使用它来找到最佳策略来了解它的力量。

本文基于 Richard S. Sutton 和 Andrew G. Barto 撰写的《强化学习》一书中的 Chapter 4。我非常感谢为本书的出版做出贡献的作者的努力。

三、求解贝尔曼方程

让我们想象一下，我们完全了解环境的动态，其中包含 |小号|国家。行动过渡概率由策略π给出。鉴于此，我们可以求解该环境的 V 函数的贝尔曼方程，该方程实际上将表示一个线性方程组，其中 |小号|变量（在 Q 函数的情况下，将有 |小号|x |答|方程式）。

该方程组的解对应于每个状态的 v 值（或每对（状态、对）的 q 值）。

举例

让我们看一个简单的环境示例，该环境具有 5 种状态，其中 T 是最终状态。蓝色数字表示转换概率，红色数字表示智能体收到的奖励。我们还将假设智能体在状态 A 中选择的相同操作（由概率 p = 0.6 的水平箭头表示）导致具有不同概率的 C 或 D（p = 0.8 和 p = 0.2）。

示例的过渡图。蓝色数字表示状态之间的转换概率，红色数字表示相应的奖励。

由于环境包含 |小号| = 5 个状态，要找到所有 v 值，我们必须求解一个由 5 个贝尔曼方程组成的方程组：

V 函数的贝尔曼方程组。

由于 T 是终末态，它的 v 值始终为 0，因此从技术上讲，我们只需要求解 4 个方程。

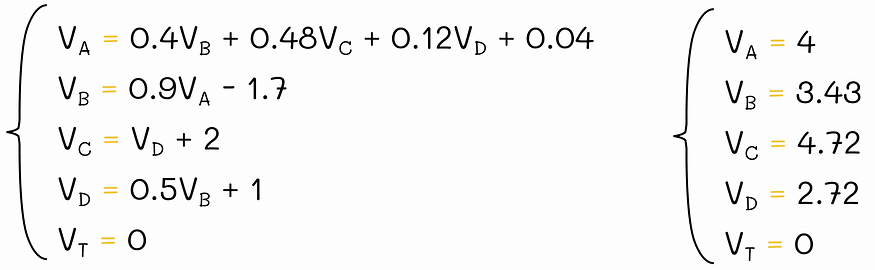
方程组的解。

求解 Q 函数的类似系统会更难，因为我们需要求解每对（状态、动作）的方程。

四、策略评估

如上例所示，以简单明了的方式求解线性方程组是获得实数 v 值的一种可能方法。但是，给定三次算法复杂度 O（n³），其中 n = |S|，它不是最优的，尤其是当状态数 |小号|很大。相反，我们可以应用迭代策略评估算法：

随机初始化所有环境状态的 v 值（v 值必须等于 0 的终端状态除外）。
使用 Bellman 方程迭代更新所有非终端状态。
重复步骤 2，直到先前和当前 v 值之间的差值太小（≤ θ）。

策略评估伪代码。资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

如果状态数 |小号|如果有限，则可以在数学上证明，在给定策略下，策略评估算法获得的迭代估计最终π收敛到实际 V 值！

状态 s ∈ S 的 v 值的单次更新称为预期更新。这个名称背后的逻辑是，更新过程考虑了 s 的所有可能的连续状态的奖励，而不仅仅是单个状态。

所有状态的更新的整个迭代称为扫描。

注意。类似的迭代算法也可以应用于Q函数的计算。

为了了解这个算法有多神奇，让我们再次强调它：

策略评估允许在给定的策略π下迭代查找 V 函数。

4.1 更新变体

策略评估算法中的更新方程可以通过两种方式实现：

通过使用两个数组：根据存储在两个单独数组中的未更改的旧值按顺序计算新值。
通过使用一个数组：计算值将立即被覆盖。因此，在同一迭代期间的后续更新将使用覆盖的新值。

在实践中，覆盖 v 值是执行更新的更可取方法，因为与双数组方法相比，新信息一旦可用于其他更新，就会立即使用。因此，v 值趋于收敛得更快。

该算法不会对每次迭代期间应更新的变量顺序施加规则，但顺序会对收敛率产生很大影响。

4.2 例描述

为了进一步了解策略评估算法在实践中是如何工作的，让我们看一下 Sutton 和 Barto 书中的示例 4.1。我们得到了一个 4 x 4 网格形式的环境，其中在每一步中，智能体等价（p = 0.25）在四个方向之一（向上、向右、向下、向左）迈出一步。

智能体从一个随机的迷宫单元开始，可以朝四个方向之一前进，每一步都获得奖励 R = -1。A4 和 D1 是终端状态。图片由作者改编。资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

如果智能体位于迷宫的边缘，并选择进入迷宫周围墙壁的方向，则其位置保持不变。例如，如果代理位于 D3 并选择向右移动，则它将在下一个状态停留在 D3。

每次移动到任何单元格都会产生 R = -1 奖励，但位于 A4 和 D1 的两个终端状态的奖励为 R = 0。最终目标是计算给定等概率策略的 V 函数。

算法

让我们将所有 V 值初始化为 0。然后，我们将运行策略评估算法的几次迭代：

不同策略评估迭代的 V 函数。图片由作者改编。资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

在某些时候，在连续迭代中，v 值之间不会有任何变化。这意味着算法已收敛到实际 V 值。对于迷宫，等概率策略下的 V 函数显示在最后一行图的右侧。

解释

假设一个根据随机策略行事的智能体从预期奖励为 -18 的单元格 C2 开始。根据 V 函数定义，-18 是智能体在剧集结束时获得的总累积奖励。由于迷宫中的每一步都会增加 -1 的奖励，因此我们可以将 v 值 18 解释为智能体在达到最终状态之前必须执行的预期步数。

五、策略改进

乍一看，这听起来可能令人惊讶，但 V 和 Q 函数可用于找到最佳策略。为了理解这一点，让我们参考迷宫示例，在该示例中，我们计算了启动随机策略的 V 函数。

5.1 V函数描述

例如，让我们以单元格 B3 为例。根据我们的随机策略，智能体可以从该状态以相等的概率向 4 个方向移动。它可能获得的预期奖励是 -14、-20、-20 和 -14。假设我们有一个选项来修改该状态的策略。为了最大化预期奖励，总是从 B3 转到 A3 或 B4 旁边，即在邻域中具有最大预期奖励的单元格中（在我们的例子中为 -14）不是合乎逻辑的吗？

来自单元格 B3 的最佳操作导致 A3 或 B4，其中预期奖励达到最大值。

这个想法是有道理的，因为位于 A3 或 B4 的位置使代理有可能一步完成迷宫。因此，我们可以包含 B3 的转换规则以派生新策略。然而，进行这样的转变以最大化预期回报是否总是最佳的？

事实上，贪婪地过渡到一个行动，其预期回报的组合在其他可能的下一个状态中是最大的，会导致更好的政策。

为了继续我们的示例，让我们对所有迷宫状态执行相同的过程：

收敛的 V 函数及其对应的贪婪策略。图片由作者改编。资料来源：

因此，我们得出了比旧政策更好的新政策。顺便说一句，我们的发现也可以通过政策改进定理推广到其他问题，该定理在强化学习中起着至关重要的作用。

5.2 政策改进定理

配方

Sutton和Barto的书中的公式简明扼要地描述了该定理：

设 π 和 π' 是任何一对确定性策略，这样，对于所有 s ∈ S，

资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

那么政策π'必须与π一样好，或者更好。也就是说，它必须从所有状态获得更大或相等的预期回报 s ∈ S：

资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

逻辑

为了理解该定理的公式，让我们假设我们可以访问在策略π下评估的给定环境的 V 函数和 Q 函数。对于这种环境，我们将创建另一个策略π'。该政策将与π完全相同，唯一的区别是，对于每个州，它将选择导致相同或更高奖励的行动。然后，该定理保证策略 π' 下的 V 函数将优于策略π下的 V 函数。

根据政策改进定理，我们总是可以通过贪婪地选择当前政策的行动来推导出更好的政策，从而为每个州带来最大的回报。

六、策略迭代

给定任何起始策略π，我们可以计算其 V 函数。此 V 函数可用于将策略改进为 π'。有了这个策略 π'，我们可以计算它的 V' 函数。此过程可以重复多次，以迭代方式生成更好的策略和值函数。

在极限中，对于有限数量的状态，这种称为策略迭代的算法会收敛到最优策略和最优值函数。

政策评估（E）和政策改进（I）之间的迭代交替。图片由作者改编。资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

如果我们将策略迭代算法应用于迷宫示例，则最佳 V 函数和策略将如下所示：

迷宫示例的最佳 V 函数和策略。图片由作者改编。资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

在这些设置中，通过获得的最优 V 函数，我们可以根据最优策略轻松估计达到最终状态所需的步数。

这个例子的有趣之处在于，我们只需要两次策略迭代就可以从头开始获取这些值（我们可以注意到，映像中的最佳策略与之前我们贪婪地将其更新为相应的 V 函数时完全相同）。在某些情况下，策略迭代算法只需要很少的迭代即可收敛。

用于更复杂的迷宫环境的最佳 V 函数和策略示例。

七、值迭代

尽管可以使用原始策略迭代算法来查找最佳策略，但速度可能很慢，主要是因为在策略评估步骤期间执行了多次扫描。此外，精确 V 函数的完整收敛过程可能需要大量扫描。

7.1 算法描述

此外，有时不需要获取精确的 v 值来产生更好的策略。前面的例子完美地证明了这一点：我们可以只执行 k = 3 次扫描，然后根据获得的 V 函数的近似值构建策略，而不是执行多次扫描。该策略与我们在 V 函数收敛后计算的策略完全相同。

前三次迭代的 V 函数和策略评估。我们可以看到，从第三次迭代开始，策略没有改变。此示例演示在某些情况下，没有必要运行策略迭代的所有迭代。图片由作者改编。一般来说，是否可以在某个时候停止策略评估算法？事实证明，是的！此外，在每个策略评估步骤中只能执行一次扫描，结果仍将收敛到最佳策略。所描述的算法称为值迭代。

我们不打算研究这个算法的证明。然而，我们可以注意到，政策评估和政策改进是两个非常相似的过程：它们都使用贝尔曼方程，除了政策改进需要最大操作才能产生更好的行动。

通过迭代执行单次策略评估扫描和单次策略改进扫描，我们可以更快地收敛到最佳状态。实际上，一旦连续 V 函数之间的差异变得微不足道，我们就可以停止算法。

根据该理论，状态的值可以按顺序更新和覆盖，而不必使用其他状态的更新值：使用以前的值不会阻止算法找到最优策略。这种技术称为引导。

7.2 异步值迭代

在某些情况下，在值迭代的每个步骤中仅执行一次扫描可能会出现问题，尤其是当状态数 |小号|很大。为了克服这个问题，可以使用算法的异步版本：而不是在整个扫描过程中系统地执行所有状态的更新，而是只以任何顺序就地更新状态值 的子集。此外，某些状态可以在更新其他状态之前多次更新。

但是，在某些时候，必须更新所有状态，以使算法能够收敛。根据该理论，所有状态必须总共更新无限次才能实现收敛，但在实践中，这方面通常被省略，因为我们并不总是对获得 100% 最优策略感兴趣。

异步值迭代存在不同的实现。在实际问题中，它们可以在算法的速度和准确性之间进行有效的权衡。

最简单的异步版本之一是在策略评估期间仅更新单个状态。

八、广义策略迭代

我们已经研究了策略迭代算法。它的想法可以用来指代强化学习中一个更广泛的术语，称为广义策略迭代（GPI）。

GPI 包括通过政策评估和政策改进过程之间的独立交替来寻找最佳政策。

几乎所有的强化学习算法都可以称为GPI。

Sutton 和 Barto 提供了一个简化的几何图形，直观地解释了 GPI 的工作原理。让我们想象一个 2D 平面，其中每个点都表示值函数和策略的组合。然后我们将画两条线：

第一行将包含对应于环境的不同 V 函数的点。
第二行将表示与各自 V 函数相关的一组贪婪策略。

政策改进向最优点的几何可视化。图片由作者改编。资料来源：强化学习。引言。第二版 |理查德·萨顿（Richard S. Sutton）和安德鲁·巴托（Andrew G. Barto）

每次我们计算当前 V 函数的贪婪策略时，我们都会向策略线靠拢，同时远离 V 函数线。这是合乎逻辑的，因为对于新的计算策略，以前的 V 函数不再适用。另一方面，每次我们执行策略评估时，我们都会朝着 V 函数线上的点的投影移动，因此我们离策略线更远：对于新的估计 V 函数，当前策略不再是最优的。整个过程再次重复。

当这两个过程相互交替时，当前的 V 函数和策略都会逐渐改善，并且在某个时刻，它们必须达到一个最优点，该点将代表 V 函数和策略线之间的交叉点。