pytorch-13_3 模型参数初始化方法：Xavier和Kaiming（HE）

2024-05-27 11:28
文章标签 参数 方法 模型 pytorch 初始化 13 xavier kaiming

本文主要是介绍pytorch-13_3 模型参数初始化方法：Xavier和Kaiming（HE），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、激活函数使用过程中的优化

不同激活函数在深层次神经网络运行时存在的不同问题

  • ReLU激活函数叠加后出现的模型失效问题，也就是Dead ReLU Problem（神经元活性失效问题）。
  • Sigmoid激活函数堆叠后出现的问题，本质上就是梯度消失所导致的问题。
  • tanh激活函数堆叠所导致的迭代过程剧烈波动的问题，也被称为迭代不平稳，需要优化迭代过程来解决。

  从本节开始，将正式进入到优化方法的具体方法部分内容。首先是关于激活函数使用过程的优化。激活函数的使用能够有效提升神经网络模型效果，但激活函数的简单叠加却会让模型出现很多问题。本节将从堆叠激活函数遇到的问题入手，讨论造成这些问题的根源，以及如何通过一些优化方法解决这些问题。

1、梯度消失与梯度爆炸

1.1 梯度消失与梯度爆炸的概念

  对于神经网络这个复杂系统来说，在模型训练过程中，一个最基础、同时也最常见的问题，就是梯度消失和梯度爆炸。

  总结一下，不同层参数的梯度在计算过程中都有很大的差异，并且这种差异是一种累乘效应，我们也可以简单理解为是一种伴随着层数增加指数级变化的差异。而这种累乘效应会导致线性层参数的一部分梯度过大而另一部分过小，从而影响模型平稳训练。而从具体原因来说，每一层参数的梯度主要和两个因素相关，其一是线性层输入数据，如 X X X或 F ( X ∗ W ) F(X*W) F(X∗W)，其二则是激活函数导函数计算结果 f ( X ∗ w 1 ) f(X*w_1) f(X∗w1​)。

1.2 sigmoid激活函数的梯度消失问题探讨

略

1.3 tanh激活函数的梯度爆炸问题探讨

略

1.4 模型参数及梯度提取方法

实操代码演示

2、梯度不平稳的解决方案

  通过对Sigmoid和tanh激活函数叠加后的模型梯度变化情况分析，我们不难发现，梯度不平稳是影响模型建模效果的非常核心的因素。

  整体来看，针对梯度不平稳的解决方案（优化方法）总共分为五类，分别是参数初始化方法、输入数据的归一化方法、衍生激活函数使用方法、学习率调度方法以及梯度下降优化方法。接下来，先介绍所有上述优化算法的一个基本理论，由Xavier Glorot在2010提出的Glorot条件。

值得注意的是，虽然不同优化算法有不同的出发点和不同的论证方式，但基本都可以从Glorot条件出发进行思考。

2.1 Zero-centered 数据的零对称属性

  • 为了确保各层网络梯度的平稳性和学习的平稳性，通常将梯度及输入数据转换为Zero-centered data。

  • 但是转换为Zero-centered data的过程中，不能将参数的初始值全部设为0，需要借助统计工具生成均值是0的随机数，也就是0均值的均匀分布或者是0均值的高斯分布。

2.2 Glorot条件：初始化参数方差满足的条件

  • 上述随机数的方差，需要满足Glorot条件（正向传播时数据方差保持一致、反向传播时参数梯度方差保持一致的条件）。满足该条件的模型能够进行有效平稳的训练。

2.3 Xavier方法：模型初始化参数设计方法

  • 模型初始化参数设计方法：Xavier方法。该方法通过满足Glorot条件创建Zero-Centered的初始化参数时参数的方差。
  • Xavier初始化能够在Sigmoid和tanh激活函数叠加的神经网络中起到一定的效果。解决Sigmoid和tanh激活函数使用过程中可能存在的梯度消失或梯度爆炸问题。

2.4 模型初始化参数的取值影响

模型初始化参数不同，会得到不同的建模结果。换句话说，模型初始化时得到的不同参数，本质上等价于在损失函数上找到了不同的初始点。而同一损失函数，初始点选取的不同会影响最终迭代结果。

  • 接下来我们通过一个实验来说明初始值的更换对模型结果的影响。在模型实例化过程中，采用不同随机数种子，就相当于选取了不同的模型初始参数。
# 创建随机数种子
torch.manual_seed(420)  # 实例化模型
relu_model3 = ReLU_class3(bias=False)              # 核心参数
num_epochs = 20
lr = 0.03# 模型训练
train_l, test_l = model_train_test(relu_model3, train_loader,test_loader,num_epochs = num_epochs, criterion = nn.MSELoss(), optimizer = optim.SGD, lr = 0.03, cla = False, eva = mse_cal)# 绘制图像，查看MSE变化情况
plt.plot(list(range(num_epochs)), train_l, label='train_mse')
plt.plot(list(range(num_epochs)), test_l, label='test_mse')
plt.legend(loc = 4)

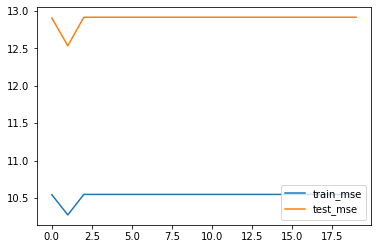
在这里插入图片描述

# 创建随机数种子
torch.manual_seed(29)  # 实例化模型
relu_model3 = ReLU_class3(bias=False)              # 核心参数
num_epochs = 20
lr = 0.03# 模型训练
train_l, test_l = model_train_test(relu_model3, train_loader,test_loader,num_epochs = num_epochs, criterion = nn.MSELoss(), optimizer = optim.SGD, lr = 0.03, cla = False, eva = mse_cal)# 绘制图像，查看MSE变化情况
plt.plot(list(range(num_epochs)), train_l, label='train_mse')
plt.plot(list(range(num_epochs)), test_l, label='test_mse')
plt.legend(loc = 4)

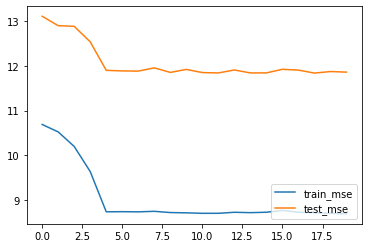
在这里插入图片描述

结果讨论：

  • 初始参数值的选取不仅会影响模型收敛速度，甚至在某些情况下还会影响模型的最终表现。
  • 造成此现象的根本原因还是在于神经网络模型在进行训练时，不确定性过多，而在一个拥有诸多不确定性的系统中再加上不确定的初始参数，初始参数的不确定性会被这个系统放大。
  • 值得一提的是，每一个epoch中的每一次迭代并不是在同一个损失函数上一步步下降的，当我们使用小批量梯度下降算法时，带入不同批的数据，实际创建的损失函数也会不同。

3、Dead ReLU Problem与学习率优化

3.1 Dead ReLU Problem直接表现

之前的ReLU叠加模型，在迭代多次后在MSE取值高位收敛的情况，其实就是出现了神经元活性失效所导致的问题。
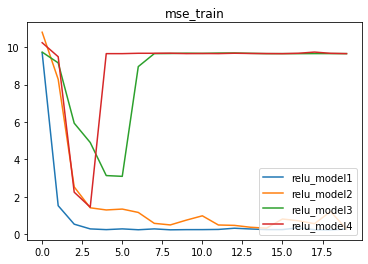
在这里插入图片描述

3.2 Dead ReLU Problem成因分析

  • 神经元活性失效问题和ReLU激活函数本身特性有关。

  • 观察ReLU激活函数函数图像与导函数图像得知，对于ReLU激活函数来说，只要激活函数接收到的数据小于0，输出结果就全是0，由于ReLU的导函数是分段常数函数且接收数据为负时导数为0，因此如果ReLU输出结果为零，则反向传播结果、也就是各层的梯度，也都是零，此时参数将无法通过迭代更新。

  • 进一步的，如果在某种参数情况下，整个训练数据集输入模型之后输出结果都是0，则在小批量梯度下降的情况下，每次再挑选出一些数据继续进行迭代，仍然无法改变输出结果是0的情况，此时参数无法得到更新、进而下次输入的小批数据结果还是零、从而梯度为0、从而参数无法更新…至此陷入死循环，模型失效、激活函数失去活性，也就出现了Dead ReLU Problem。
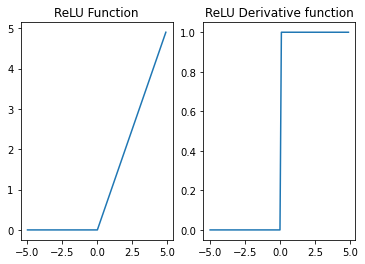
    在这里插入图片描述

  • 出现Dead ReLU Problem问题的概率，伴随ReLU层的增加而增加的。在多层ReLU嵌套的情况下，输出结果 y ^ \hat y y^​取值为0的概率就更大了，出现Dead ReLU Problem的概率也就更高了。而同时，根据各层参数的梯度计算公式，只要其中任意一层输出结果是0，则所有层参数的梯度均为0。

3.3 调整学习率：缓解Dead ReLU Problem

  在所有的解决Dead ReLU Problem的方法中，最简单的一种方法就是调整学习率。尽管我们知道，ReLU叠加越多层越容易出现神经元活性失效，但我们可以简单通过降低学习率的方法来缓解神经元活性失效的问题。甚至可以说这是一种通用且有效的方法。
  学习率作为模型重要的超参数，会在各方面影响模型效果，此前我们曾介绍学习率越小、收敛速度就越慢，而学习率过大、则又容易跳过最小值点造成模型结果震荡。对于ReLU激活函数来说，参数“稍有不慎”就容易落入输出值全为0的陷阱，因此训练过程需要更加保守，采用更小的学习率逐步迭代。当然学习率减少就必然需要增加迭代次数，但由于ReLU激活函数计算过程相对简单，增加迭代次数并不会显著增加计算量。

# 核心参数
lr = 0.030# 核心参数
lr = 0.001

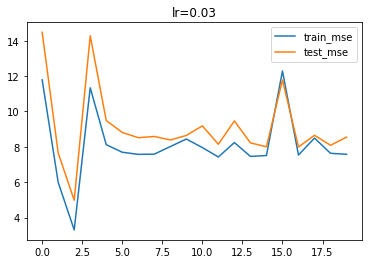
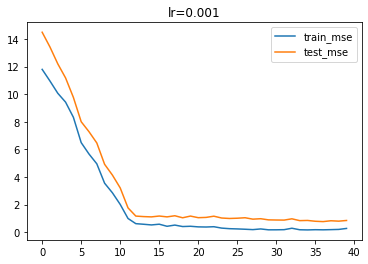
在这里插入图片描述
在这里插入图片描述
通过调小学习率，模型更能够避开神经元活性失效陷阱。

4、nn.Sequential快速建模方法及nn.init模型参数自定义方法

# 设置随机数种子
torch.manual_seed(25)# 一、nn.Sequential快速构建模型
relu_test = nn.Sequential(nn.Linear(2, 2, bias=False), nn.ReLU(), nn.Linear(2, 1, bias=False))# 二、nn.init初始化模型参数
# (1)`.nn.init.uniform_`方法，新生成的参数服从均匀分布
nn.init.uniform_(list(relu_test.parameters())[0], 0, 1)         # 设置参数值为均匀分布在0，1区间内的随机数# `torch.nn.init.xavier_uniform_`
nn.init.xavier_uniform_(list(relu_test.parameters())[0])        # Xavier均匀分布的参数创建# `torch.nn.init.kaiming_uniform_`
nn.init.kaiming_uniform_(list(relu_test.parameters())[0])        # HE均匀分布的参数创建# (2)`.nn.init.normal_`方法，新生成的参数服从正态分布
nn.init.normal_(list(relu_test.parameters())[0], 0, 1)          # 服从均值为0、标准差为1的正态分布# `torch.nn.init.xavier_normal_`
nn.init.xavier_normal_(list(relu_test.parameters())[0])        # Xavier正态分布的参数创建# `torch.nn.init.kaiming_normal_`
nn.init.kaiming_normal_(list(relu_test.parameters())[0])        # HE正态分布的参数创建# (3)`.nn.init.constant_`方法，新生成的参数值为某一常数
nn.init.constant_(list(relu_test.parameters())[0], 1)           # 参数全为1

5、Xavier参数初始化方法

5.1 Xavier均匀分布的参数创建nn.init.xavier_uniform_

5.1.1 Sigmoid_class3
# 设置随机数种子
torch.manual_seed(420)  # 创建最高项为2的多项式回归数据集
features, labels = tensorGenReg(w=[2, -1], bias=False, deg=2)# 进行数据集切分与加载
train_loader, test_loader = split_loader(features, labels)# 初始核心参数
lr = 0.03
num_epochs = 20# 实例化模型
sigmoid_model3 = Sigmoid_class3()                   # 保留原参数
sigmoid_model3_init = Sigmoid_class3()              # 使用Xavier初始化参数# 修改init模型初始参数
for m in sigmoid_model3_init.modules():if isinstance(m, nn.Linear):nn.init.xavier_uniform_(m.weight)           # 使用Xavier初始化参数# 创建模型容器
model_l = [sigmoid_model3, sigmoid_model3_init]           
name_l = ['sigmoid_model3', 'sigmoid_model3_init']# 多个模型训练
train_l, test_l = model_comparison(model_l = model_l, name_l = name_l, train_data = train_loader,test_data = test_loader,num_epochs = 2, criterion = nn.MSELoss(), optimizer = optim.SGD, lr = lr, cla = False, eva = mse_cal)# 模型梯度
weights_vp(sigmoid_model3, att="grad")
weights_vp(sigmoid_model3_init, att="grad")

在这里插入图片描述
在这里插入图片描述

我们发现，在num_epochs取值为2的时候（只迭代了一轮），经过Xavier初始化的模型梯度整体更加稳定，并且没有出现梯度消失的情况，反观原始模型sigmoid_model2，第一层的梯度已经非常小了，已经出现了梯度消失的倾向。而我们知道，各层梯度的情况就代表着模型学习的状态，很明显经过初始化的模型各层都处于平稳学习状态，此时模型收敛速度较快。我们也可以通过MSE曲线进行验证。

# 训练误差 损失函数
for i, name in enumerate(name_l):plt.plot(list(range(num_epochs)), train_l[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')# 测试误差 损失函数
for i, name in enumerate(name_l):plt.plot(list(range(num_epochs)), test_l[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')

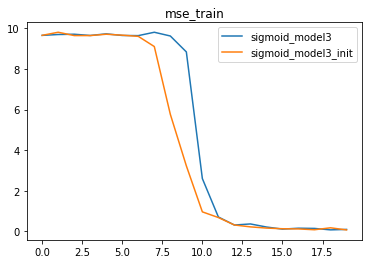
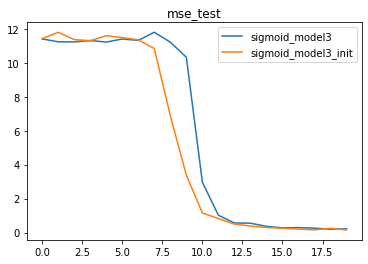
在这里插入图片描述
在这里插入图片描述
  由此我们可知，Xavier初始化的作用核心在于保证各层梯度取值的平稳分布，从而确保各层模型学习的有效性，最终在模型结果的表现上，经过Xavier初始化参数的模型学习效率更高、收敛速度更快。上述结果也验证了Xavier初始化有效性。

5.1.2 Sigmoid_class4
# 设置随机数种子
torch.manual_seed(24)  # 实例化模型
sigmoid_model4 = Sigmoid_class4()                   # 保留原参数
sigmoid_model4_init = Sigmoid_class4()              # 使用Xavier初始化参数# 修改init模型初始参数
for m in sigmoid_model4_init.modules():if isinstance(m, nn.Linear):nn.init.xavier_uniform_(m.weight)# 创建模型容器
model_l = [sigmoid_model4, sigmoid_model4_init]           
name_l = ['sigmoid_model4', 'sigmoid_model4_init']# 核心参数
lr = 0.03
num_epochs = 40# 模型训练
train_l, test_l = model_comparison(model_l = model_l, name_l = name_l, train_data = train_loader,test_data = test_loader,num_epochs = num_epochs, criterion = nn.MSELoss(), optimizer = optim.SGD, lr = lr, cla = False, eva = mse_cal)# 训练误差 损失函数
for i, name in enumerate(name_l):plt.plot(list(range(num_epochs)), train_l[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')# 测试误差 损失函数
for i, name in enumerate(name_l):plt.plot(list(range(num_epochs)), test_l[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')

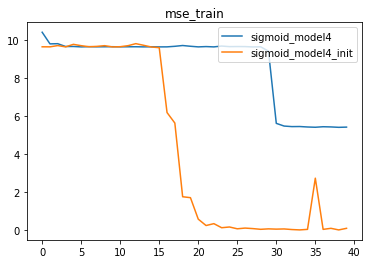
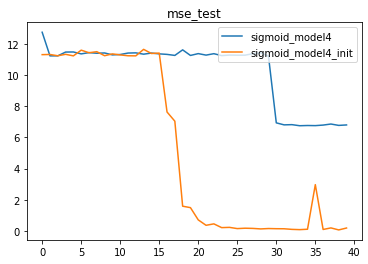
在这里插入图片描述
在这里插入图片描述

  • sigmoid_model4是出现严重梯度消失的模型，由于前几层基本丧失学习能力，sigmoid_model4本身效果并不好。但加入Xavier初始化之后，我们发现，init模型能够极大程度规避梯度消失问题，从而获得更好的效果。
  • 不过正如此前所说，相比于sigmoid激活函数，Xavier初始化方法更适用于tanh激活函数，核心原因在于tanh激活函数本身能够生成Zero-centered
    Data，配合Xavier初始化生成的参数，能够更好的确保各层梯度平稳、确保各层平稳学习。
5.1.3 tanh_class3
# 设置随机数种子
torch.manual_seed(420)  # 实例化模型
tanh_model3 = tanh_class3()                   # 保留原参数
tanh_model3_init = tanh_class3()              # 使用Xavier初始化参数# 修改init模型初始参数
for m in tanh_model3_init.modules():if isinstance(m, nn.Linear):nn.init.xavier_uniform_(m.weight)# 创建模型容器
model_l = [tanh_model3, tanh_model3_init]           
name_l = ['tanh_model3', 'tanh_model3_init']# 核心参数
lr = 0.03
num_epochs = 40# 模型训练
train_l, test_l = model_comparison(model_l = model_l, name_l = name_l, train_data = train_loader,test_data = test_loader,num_epochs = num_epochs, criterion = nn.MSELoss(), optimizer = optim.SGD, lr = lr, cla = False, eva = mse_cal)# 查看模型梯度
weights_vp(tanh_model3, att="grad")
weights_vp(tanh_model3_init, att="grad")

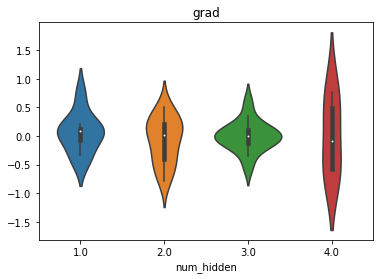
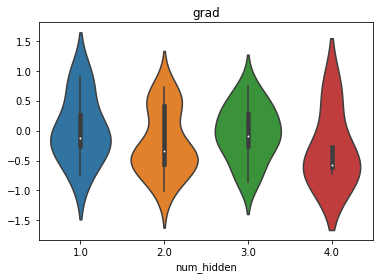
在这里插入图片描述
在这里插入图片描述

同样，能够看出经过Xavier参数初始化后的模型梯度更加平稳，进而我们判断，经过初始化之后的模型初始迭代时收敛速度更快

# 训练误差
for i, name in enumerate(name_l):plt.plot(list(range(num_epochs)), train_l[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')# 测试误差
for i, name in enumerate(name_l):plt.plot(list(range(num_epochs)), test_l[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')

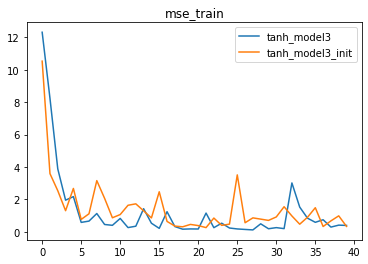
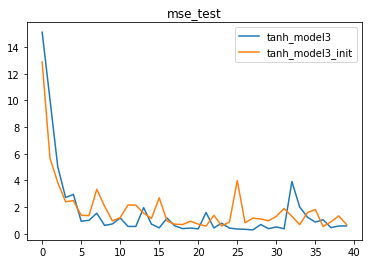
在这里插入图片描述
在这里插入图片描述

同样我们能够发现，模型收敛速度更快，迭代多轮之后也变得更加稳定。

5.2 Xavier高斯分布的参数创建nn.init.xavier_normal_

5.2.1 Sigmoid_class3

略

5.2.2 Sigmoid_class4

略

5.2.3 tanh_class3

略

6、HE参数初始化：Kaiming方法

  • HE参数初始化：Kaiming方法，是目前通用的针对ReLU激活函数的初始化参数方法。

  • 尽管Xavier初始化能够在Sigmoid和tanh激活函数叠加的神经网络中起到一定的效果，但由于ReLU激活函数属于非饱和类激活函数，并不会出现类似Sigmoid和tanh激活函数使用过程中可能存在的梯度消失或梯度爆炸问题。

  • 因为ReLU激活函数的不饱和特性，ReLU激活函数的叠加极有可能出现神经元活性消失的问题，很明显，该类问题无法通过Xavier初始化解决。

  • 但是对参数的初始值进行合理设置，仍然是保证模型有效性的有效方法，同样也能一定程度上解决ReLU激活函数的神经元活性消失问题。

  • 目前通用的针对ReLU激活函数的初始化参数方法，是由何凯明在2015年的《Delving
    Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet
    Classification》一文中所提出的HE初始化方法，也被称为Kaiming方法。原文地址。

6.1 对ReLU_class3使用nn.init.kaiming_uniform_ 均匀分布

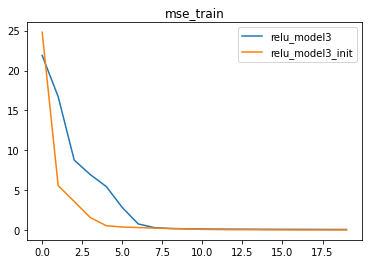
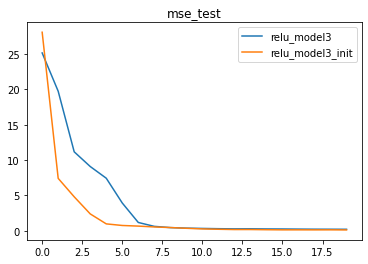
在这里插入图片描述
在这里插入图片描述
我们发现，使用HE初始化之后模型收敛速度明显提升。

6.2 对ReLU_class3使用nn.init.kaiming_normal_ 高斯分布

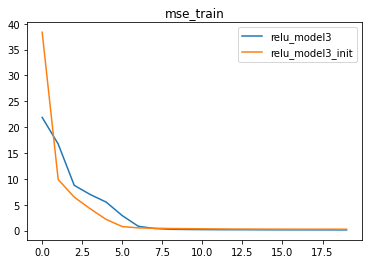
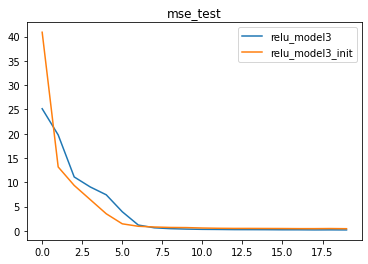
在这里插入图片描述
在这里插入图片描述
同样，经过HE初始化后的参数，模型收敛速度更快，也证明了HE初始化的有效性。

7、总结与讨论

7.1 激活函数问题及优化

  • sigmoid和tanh，可能出现梯度消失和梯度爆炸问题，通过Xavier参数初始化进行优化。
  • relu，可能出现神经元活性消失的问题，通过调节学习率或者HE参数初始化进行优化。

7.1 参数初始化的方法总结

# 设置随机数种子
torch.manual_seed(25)# 一、nn.Sequential快速构建模型
relu_test = nn.Sequential(nn.Linear(2, 2, bias=False), nn.ReLU(), nn.Linear(2, 1, bias=False))# 二、nn.init初始化模型参数
# (1)`.nn.init.uniform_`方法，新生成的参数服从均匀分布
nn.init.uniform_(list(relu_test.parameters())[0], 0, 1)         # 设置参数值为均匀分布在0，1区间内的随机数# `torch.nn.init.xavier_uniform_`
nn.init.xavier_uniform_(list(relu_test.parameters())[0])        # Xavier均匀分布的参数创建# `torch.nn.init.kaiming_uniform_`
nn.init.kaiming_uniform_(list(relu_test.parameters())[0])        # HE均匀分布的参数创建# (2)`.nn.init.normal_`方法，新生成的参数服从正态分布
nn.init.normal_(list(relu_test.parameters())[0], 0, 1)          # 服从均值为0、标准差为1的正态分布# `torch.nn.init.xavier_normal_`
nn.init.xavier_normal_(list(relu_test.parameters())[0])        # Xavier正态分布的参数创建# `torch.nn.init.kaiming_normal_`
nn.init.kaiming_normal_(list(relu_test.parameters())[0])        # HE正态分布的参数创建# (3)`.nn.init.constant_`方法，新生成的参数值为某一常数
nn.init.constant_(list(relu_test.parameters())[0], 1)           # 参数全为1

7.2 讨论：参数初始化的作用局限

  截止目前，我们讨论了围绕Glorot条件进行的参数初始化方法，当然，合理的设置初始参数值能够一定程度上使得模型各层都得到有效的学习，模型训练过程更加平稳、收敛速度也更快。但由于我们设置的是初始条件，伴随着模型不断训练，由于受到激活函数导函数本身特性影响，仍然有可能在迭代过程中出现梯度不均衡的现象。
  然而模型一旦开始训练，我们是不能手动参与修改模型参数的。那此时应该如何处理梯度不均衡的问题呢？我们知道，影响梯度计算的三个核心因素，分别是参数状态值、激活值和输入的数据，参数状态值由模型迭代的数学过程决定，激活值很大程度上由我们所选取的激活函数决定，如果从Glorot条件入手，我们就只剩下一个可以人工修改的选项：每一个线性层接收到的数据。

这篇关于pytorch-13_3 模型参数初始化方法：Xavier和Kaiming（HE）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1007339。

相关文章

Spring Security基于数据库的ABAC属性权限模型实战开发教程

Spring Security基于数据库的ABAC属性权限模型实战开发教程

《SpringSecurity基于数据库的ABAC属性权限模型实战开发教程》：本文主要介绍SpringSecurity基于数据库的ABAC属性权限模型实战开发教程,本文给大家介绍的非常详细,对大... 目录1. 前言2. 权限决策依据RBACABAC综合对比3. 数据库表结构说明4. 实战开始5. MyBA
阅读更多...
Spring Security方法级安全控制@PreAuthorize注解的灵活运用小结

Spring Security方法级安全控制@PreAuthorize注解的灵活运用小结

《SpringSecurity方法级安全控制@PreAuthorize注解的灵活运用小结》本文将带着大家讲解@PreAuthorize注解的核心原理、SpEL表达式机制,并通过的示例代码演示如... 目录1. 前言2. @PreAuthorize 注解简介3. @PreAuthorize 核心原理解析拦截与
阅读更多...
一文详解JavaScript中的fetch方法

一文详解JavaScript中的fetch方法

《一文详解JavaScript中的fetch方法》fetch函数是一个用于在JavaScript中执行HTTP请求的现代API,它提供了一种更简洁、更强大的方式来处理网络请求,：本文主要介绍Jav... 目录前言什么是 fetch 方法基本语法简单的 GET 请求示例代码解释发送 POST 请求示例代码解释
阅读更多...
Feign Client超时时间设置不生效的解决方法

Feign Client超时时间设置不生效的解决方法

《FeignClient超时时间设置不生效的解决方法》这篇文章主要为大家详细介绍了FeignClient超时时间设置不生效的原因与解决方法,具有一定的的参考价值,希望对大家有一定的帮助... 在使用Feign Client时，可以通过两种方式来设置超时时间：1.针对整个Feign Client设置超时时间
阅读更多...
C/C++错误信息处理的常见方法及函数

C/C++错误信息处理的常见方法及函数

《C/C++错误信息处理的常见方法及函数》C/C++是两种广泛使用的编程语言,特别是在系统编程、嵌入式开发以及高性能计算领域,：本文主要介绍C/C++错误信息处理的常见方法及函数,文中通过代码介绍... 目录前言1. errno 和 perror()示例：2. strerror()示例：3. perror(
阅读更多...
CSS去除a标签的下划线的几种方法

CSS去除a标签的下划线的几种方法

《CSS去除a标签的下划线的几种方法》本文给大家分享在CSS中，去除a标签（超链接）的下划线的几种方法，本文给大家介绍的非常详细，感兴趣的朋友一起看看吧... 在 css 中，去除a标签（超链接）的下划线主要有以下几种方法：使用text-decoration属性通用选择器设置：使用a标签选择器，将tex
阅读更多...
C++变换迭代器使用方法小结

C++变换迭代器使用方法小结

《C++变换迭代器使用方法小结》本文主要介绍了C++变换迭代器使用方法小结,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧... 目录1、源码2、代码解析代码解析：transform_iterator1. transform_iterat
阅读更多...
C++中std::distance使用方法示例

C++中std::distance使用方法示例

《C++中std::distance使用方法示例》std::distance是C++标准库中的一个函数,用于计算两个迭代器之间的距离,本文主要介绍了C++中std::distance使用方法示例,具... 目录语法使用方式解释示例输出：其他说明：总结std::distance&n编程bsp;是 C++ 标准
阅读更多...
Linux换行符的使用方法详解

Linux换行符的使用方法详解

《Linux换行符的使用方法详解》本文介绍了Linux中常用的换行符LF及其在文件中的表示,展示了如何使用sed命令替换换行符,并列举了与换行符处理相关的Linux命令,通过代码讲解的非常详细,需要的... 目录简介检测文件中的换行符使用 cat -A 查看换行符使用 od -c 检查字符换行符格式转换将
阅读更多...
SpringBoot实现数据库读写分离的3种方法小结

SpringBoot实现数据库读写分离的3种方法小结

《SpringBoot实现数据库读写分离的3种方法小结》为了提高系统的读写性能和可用性,读写分离是一种经典的数据库架构模式,在SpringBoot应用中,有多种方式可以实现数据库读写分离,本文将介绍三... 目录一、数据库读写分离概述二、方案一：基于AbstractRoutingDataSource实现动态
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2