本文主要是介绍【机器学习论文阅读笔记】Robust Recovery of Subspace Structures by Low-Rank Representation,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
终于要轮到自己汇报了好崩溃。。盯着论文准备开始做汇报ppt感觉一头乱麻,决定还是写博客理清思路再说吧
参考资料:
论文原文:arxiv.org/pdf/1010.2955
RPCA参考文章:RPCA - 知乎 (zhihu.com)
谱聚类参考文章:谱聚类(spectral clustering)原理总结 - 刘建平Pinard - 博客园 (cnblogs.com)
一、问题描述
该篇论文提出了一种名为LRR(Low-Rank Representation)的目标函数,为了解决以下问题:
给定一组从多个子空间的并集中近似抽取的数据样本(向量),我们的目标是将样本聚类到它们各自的子空间中,并去除可能的异常值。
Given a set of data samples (vectors) approximately drawn from a union of multiple subspaces, our goal is to cluster the samples into their respective subspaces and remove possible outliers as well.
什么叫数据样本是从多个子空间的并集中近似抽取的?

如图所示,当我们的每个数据点的特征数量为3时,样本空间就是三维的空间
左边的图就表示严格地从一个二维平面中和两条一维的直线上抽取数据点;右边的图则表示近似地从相同的这三个子空间中抽取数据点。
而典型的异常值有以下几种类型:

(a)为噪声,表示数据在子空间周围受到轻微扰动
(b)为随机损坏,表示有随机的部分数据被严重损坏
©为特定的损坏,表示有数据样本的一部分(即数据的列)远离子空间
二、子空间恢复
1. 低秩表示
首先关注怎么把子空间中的数据从误差中恢复出来

我们把原始的数据矩阵 X X X 表示为两个矩阵的加和:
X = X 0 + E 0 X = X_0 + E_0 X=X0+E0
其中, X 0 X_0 X0就是恢复后的矩阵, E 0 E_0 E0就是代表异常值的矩阵
我们看下这两个矩阵分别有什么特点,举一个比较简单的例子

像左侧这样一个被损坏的数据,我们可以将其分解为一个低秩(各列之间相关性较强)的矩阵,还有一个稀疏的矩阵
为了能够完成这一目标,我们定义优化目标如下:
m i n D , E r a n k ( D ) + λ ∣ ∣ E ∣ ∣ l s . t . X = D + E min_{D, E} \space rank(D) + \lambda ||E||_l \quad s.t. \quad X = D + E minD,E rank(D)+λ∣∣E∣∣ls.t.X=D+E
其中, D D D表示恢复后的矩阵, ∣ ∣ E ∣ ∣ l ||E||_l ∣∣E∣∣l表示特定的正则化项, l l l由异常的类型决定:
当异常值为一中提到的
(a) 噪声: ∣ ∣ E ∣ ∣ l ||E||_l ∣∣E∣∣l 为 ∣ ∣ E ∣ ∣ F ||E||_F ∣∣E∣∣F
(b) 随机损坏: ∣ ∣ E ∣ ∣ l ||E||_l ∣∣E∣∣l 为 ∣ ∣ E ∣ ∣ 0 ||E||_0 ∣∣E∣∣0
© 特定损坏: ∣ ∣ E ∣ ∣ l ||E||_l ∣∣E∣∣l 为 ∣ ∣ E ∣ ∣ 2 , 0 ||E||_{2,0} ∣∣E∣∣2,0
其实这上面的公式是被Robust PCA所采用的,而且这个公式隐式地假设了底层的数据是单一的低秩子空间的结构
当我们的数据是从多个子空间的并集 ∪ i = 1 k S i \cup_{i=1}^k S_i ∪i=1kSi中提取出来的时,使用上述公式,就是把数据当作从一个单一的子空间 S = ∑ i = 1 k S i S = \sum_{i=1}^k S_i S=∑i=1kSi中采样
然而, ∑ i = 1 k S i \sum_{i=1}^k S_i ∑i=1kSi是比 ∪ i = 1 k S i \cup_{i=1}^k S_i ∪i=1kSi要大的多的,所以使用上述目标函数会不够精确,不能很好地考虑到单个子空间的细节
对此,我们使用以下优化目标代替:
m i n Z , E r a n k ( Z ) + λ ∣ ∣ E ∣ ∣ l s . t . X = A Z + E min_{Z, E} \space rank(Z) + \lambda ||E||_l \quad s.t. \quad X = AZ + E minZ,E rank(Z)+λ∣∣E∣∣ls.t.X=AZ+E
其中, A A A是一个横跨数据空间的“字典”。我们将上述优化目标关于 Z Z Z的解 Z ∗ Z^* Z∗ 称作 X X X在字典 A A A中的低最低秩表示(lowest rank representation)
在字典学习中,我们会利用一个字典 A A A,得到数据 X X X的稀疏表示 α \alpha α,从而提取出数据中最本质的特征,用更少的资源表示尽可能多的知识:
X = A α X = A \alpha X=Aα
当 A = I A = I A=I时,后面的公式就会返回前面的形式。所以LRR可以看作是RPCA泛化的版本,而RPCA使用标准基作为字典
2. 分析LRR问题
由于秩函数的离散性,优化问题难以解决。实际上,在秩最小化的问题中,人们常用 核范数(一个矩阵的奇异值之和) 代替:
m i n Z , E ∣ ∣ Z ∣ ∣ ∗ + λ ∣ ∣ E ∣ ∣ l s . t . X = A Z + E min_{Z, E} \space ||Z||_* + \lambda ||E||_l \quad s.t. \quad X = AZ + E minZ,E ∣∣Z∣∣∗+λ∣∣E∣∣ls.t.X=AZ+E
由于 l 1 l_1 l1范数和 l 2 , 1 l_{2,1} l2,1范数分别是 l 0 l_0 l0范数和 l 2 , 0 l_{2,0} l2,0范数的良好松弛,将优化问题写作如下形式:
m i n Z , E ∣ ∣ Z ∣ ∣ ∗ + λ ∣ ∣ E ∣ ∣ 2 , 1 s . t . X = A Z + E min_{Z, E} \space ||Z||_* + \lambda ||E||_{2,1} \quad s.t. \quad X = AZ + E minZ,E ∣∣Z∣∣∗+λ∣∣E∣∣2,1s.t.X=AZ+E
将其转化为等价问题如下:
m i n Z , E , J ∣ ∣ J ∣ ∣ ∗ + λ ∣ ∣ E ∣ ∣ 2 , 1 s . t . X = A Z + E , J = Z min_{Z, E, J} \space ||J||_* + \lambda ||E||_{2,1} \quad s.t. \quad X = AZ + E, J = Z minZ,E,J ∣∣J∣∣∗+λ∣∣E∣∣2,1s.t.X=AZ+E,J=Z
我也不知道为什么要引入一个 J = Z J = Z J=Z,多这个变量有什么必要吗
利用增广拉格朗日乘子法(ALM),优化目标转化为最小化以下拉格朗日函数:
L = ∣ ∣ J ∣ ∣ ∗ + λ ∣ ∣ E ∣ ∣ 2 , 1 + t r ( Y 1 T ( X − A Z − E ) ) + t r ( Y 2 T ( J − Z ) ) + μ 2 ( ∣ ∣ X − A Z − E ∣ ∣ F 2 + ∣ ∣ J − Z ∣ ∣ F 2 ) \mathcal{L} = ||J||_* + \lambda ||E||_{2,1} + tr(Y_1^T (X - AZ - E)) + \\ \qquad tr(Y_2^T ( J - Z)) + \frac{\mu}{2} ( || X - AZ - E ||_F^2 + || J - Z ||_F^2 ) L=∣∣J∣∣∗+λ∣∣E∣∣2,1+tr(Y1T(X−AZ−E))+tr(Y2T(J−Z))+2μ(∣∣X−AZ−E∣∣F2+∣∣J−Z∣∣F2)
算法如下:

其中,求解第一步利用的是某篇引用的方法:Singular Value Thresholding (SVT) operator
求解第二步过程如下:
由 L = ∣ ∣ J ∣ ∣ ∗ + λ ∣ ∣ E ∣ ∣ 2 , 1 + t r ( Y 1 T ( X − A Z − E ) ) + t r ( Y 2 T ( J − Z ) ) + μ 2 ( ∣ ∣ X − A Z − E ∣ ∣ F 2 + ∣ ∣ J − Z ∣ ∣ F 2 ) \mathcal{L} = ||J||_* + \lambda ||E||_{2,1} + tr(Y_1^T (X - AZ - E)) + \\ \qquad tr(Y_2^T ( J - Z)) + \frac{\mu}{2} ( || X - AZ - E ||_F^2 + || J - Z ||_F^2 ) L=∣∣J∣∣∗+λ∣∣E∣∣2,1+tr(Y1T(X−AZ−E))+tr(Y2T(J−Z))+2μ(∣∣X−AZ−E∣∣F2+∣∣J−Z∣∣F2)
令 ∂ L ∂ Z = − A T Y 1 + Y 2 + μ 2 ( − 2 A T ( X − A Z − E ) + 2 Z ) = 0 \frac{\partial \mathcal{L}}{\partial Z} = -A^T Y_1 + Y_2 + \frac{\mu}{2} (-2A^T( X -AZ - E) + 2Z) =0 ∂Z∂L=−ATY1+Y2+2μ(−2AT(X−AZ−E)+2Z)=0
得到
( A T A + I ) Z − A T ( X − E ) = 1 μ ( A T Y 1 − Y 2 ) (A^TA + I)Z - A^T(X - E) = \frac{1}{\mu} (A^T Y_1 - Y_2) (ATA+I)Z−AT(X−E)=μ1(ATY1−Y2)
Z = ( A T A + I ) − 1 ( A T ( X − E ) + 1 μ ( A T Y 1 − Y 2 ) ) Z = (A^TA + I)^{-1} (A^T(X - E) + \frac{1}{\mu} (A^T Y_1 - Y_2)) Z=(ATA+I)−1(AT(X−E)+μ1(ATY1−Y2))
求解第三步利用的是以下引理:
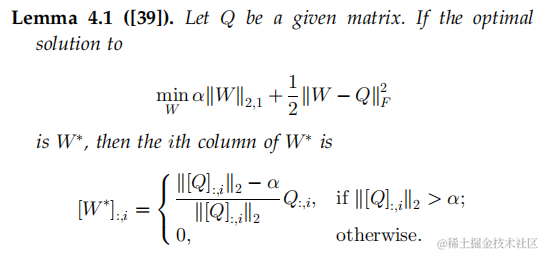
当固定其他变量,对 E E E进行迭代时,问题如下:
a r g m i n E λ μ ∣ ∣ E ∣ ∣ 2 , 1 + 1 2 ∣ ∣ E − ( X − A Z − Y 1 μ ) ∣ ∣ F 2 argmin_E \frac{\lambda}{\mu} ||E||_{2,1} + \frac{1}{2}||E - (X - AZ - \frac{Y_1}{\mu})||_F^2 argminEμλ∣∣E∣∣2,1+21∣∣E−(X−AZ−μY1)∣∣F2
三、子空间分割
将 X X X作为字典 A A A,即 A = X A = X A=X,上述优化目标可写作:
m i n Z , E ∣ ∣ Z ∣ ∣ ∗ + λ ∣ ∣ E ∣ ∣ 2 , 1 s . t . X = X Z + E min_{Z, E} \space ||Z||_* + \lambda ||E||_{2,1} \quad s.t. \quad X = XZ + E minZ,E ∣∣Z∣∣∗+λ∣∣E∣∣2,1s.t.X=XZ+E
由于当带有skinny SVD U 0 Σ 0 V 0 T U_0 \Sigma_0 V_0^T U0Σ0V0T的 X 0 X_0 X0是严格从多个子空间的并集中提取的数据样本的集合,子空间的隶属度由行空间决定,并且子空间相互独立时,有以下结论:
V 0 V 0 T V_0 V_0^T V0V0T是块对角矩阵,且当且仅当第i个样本和第j个样本来自同一子空间时, V 0 V 0 T V_0 V_0^T V0V0T的 ( i , j ) (i, j) (i,j)位置的元素非零
故可以利用 V 0 V 0 T V_0 V_0^T V0V0T做子空间分割
我们先获得对上述优化目标的解 ( Z ∗ , E ∗ ) (Z^*, E^*) (Z∗,E∗),令 Z ∗ = U ∗ Σ ∗ ( V ∗ ) T Z^* = U^* \Sigma^* (V^*)^T Z∗=U∗Σ∗(V∗)T
相对地,我们使用 U ∗ ( U ∗ ) T U^* (U^*)^T U∗(U∗)T从列空间入手做子空间分割,并定义亲和矩阵(affinity matrix)如下:
W i , j = ( [ U ~ ∗ ( U ~ ∗ ) T ] i , j ) 2 W_{i, j} = ([\tilde{U}^* (\tilde{U}^*)^T]_{i, j})^2 Wi,j=([U~∗(U~∗)T]i,j)2
其中, U ~ ∗ = U ∗ ( Σ ∗ ) 1 2 \tilde{U}^* = U^* (\Sigma^*)^{\frac{1}{2}} U~∗=U∗(Σ∗)21,原文说是为了对损坏数据有更好的性能,保证亲和矩阵的值都是正的(没理解)
最后再利用谱聚类算法比如NCut(Normalized Cuts)对 W W W做切图聚类
NCut的定义见前言中的参考文章
整体的算法流程如下:

由于执行NCut算法要先确定子空间数 k k k,可以通过计算 W W W的拉普拉斯矩阵 L L L,由 L L L的零奇异值个数得到 k k k
但是实际情况下亲和矩阵只是接近于块对角矩阵,因此论文中还提出了软阈值的方法确定 k k k


这篇关于【机器学习论文阅读笔记】Robust Recovery of Subspace Structures by Low-Rank Representation的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







