本文主要是介绍代码随想录算法训练营第五十天||309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
一、309.最佳买卖股票时机含冷冻期
思路
二、714.买卖股票的最佳时机含手续费
思路
一、309.最佳买卖股票时机含冷冻期
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
- 输入: [1,2,3,0,2]
- 输出: 3
- 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
思路
这道题主要是要定义四个状态:持有股票状态、保持卖出股票状态、今天卖出股票、冷冻期。
动规五部曲,分析如下:
1.确定dp数组以及下标的含义
dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
其实本题很多同学搞的比较懵,是因为出现冷冻期之后,状态其实是比较复杂度,例如今天买入股票、今天卖出股票、今天是冷冻期,都是不能操作股票的。
具体可以区分出如下四个状态:
- 状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
- 不持有股票状态,这里就有两种卖出股票状态
- 状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
- 状态三:今天卖出股票
- 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
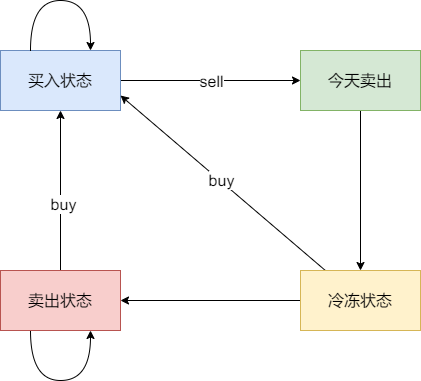
j的状态为:
- 0:状态一
- 1:状态二
- 2:状态三
- 3:状态四
很多题解为什么讲的比较模糊,是因为把这四个状态合并成三个状态了,其实就是把状态二和状态四合并在一起了。
从代码上来看确实可以合并,但从逻辑上分析合并之后就很难理解了,所以我下面的讲解是按照这四个状态来的,把每一个状态分析清楚。
2.确定递推公式
达到买入股票状态(状态一)即:dp[i][0],有两个具体操作:
- 操作一:前一天就是持有股票状态(状态一),dp[i][0] = dp[i - 1][0]
- 操作二:今天买入了,有两种情况
- 前一天是冷冻期(状态四),dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态(状态二),dp[i - 1][1] - prices[i]
那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
达到保持卖出股票状态(状态二)即:dp[i][1],有两个具体操作:
- 操作一:前一天就是状态二
- 操作二:前一天是冷冻期(状态四)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
达到今天就卖出股票状态(状态三),即:dp[i][2] ,只有一个操作:
昨天一定是持有股票状态(状态一),今天卖出
即:dp[i][2] = dp[i - 1][0] + prices[i];
达到冷冻期状态(状态四),即:dp[i][3],只有一个操作:
昨天卖出了股票(状态三)
dp[i][3] = dp[i - 1][2];
3.dp数组如何初始化
这里主要讨论一下第0天如何初始化。
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],一定是当天买入股票。
保持卖出股票状态(状态二),这里其实从 「状态二」的定义来说 ,很难明确应该初始多少,这种情况我们就看递推公式需要我们给他初始成什么数值。
如果i为1,第1天买入股票,那么递归公式中需要计算 dp[i - 1][1] - prices[i] ,即 dp[0][1] - prices[1],那么大家感受一下 dp[0][1] (即第0天的状态二)应该初始成多少,只能初始为0。想一想如果初始为其他数值,是我们第1天买入股票后 手里还剩的现金数量是不是就不对了。
今天卖出了股票(状态三),同上分析,dp[0][2]初始化为0,dp[0][3]也初始为0。
4.确定遍历顺序
从递归公式上可以看出,dp[i] 依赖于 dp[i-1],所以是从前向后遍历。
5.举例推导dp数组
以 [1,2,3,0,2] 为例,dp数组如下:
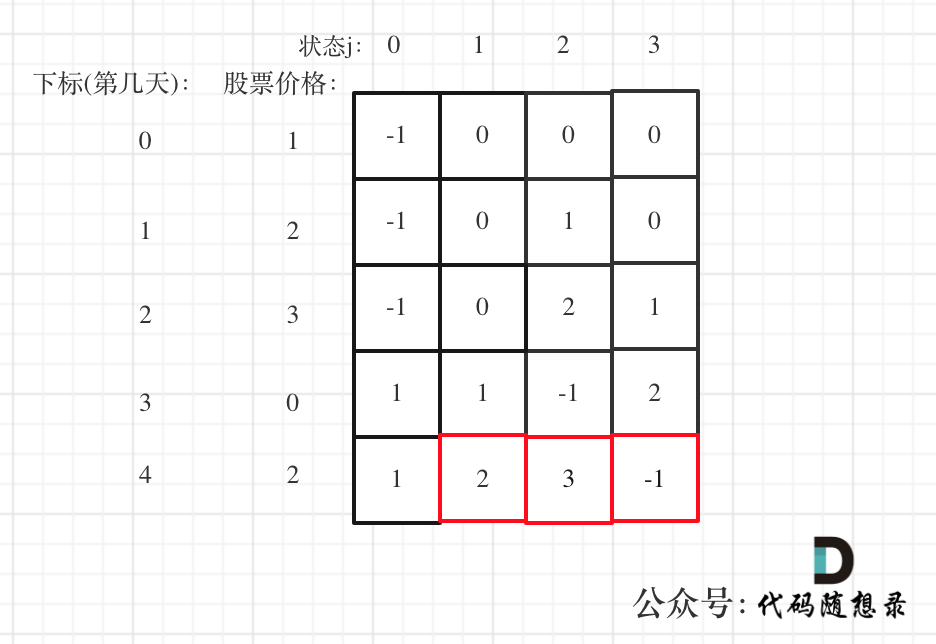
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
class Solution {public int maxProfit(int[] prices) {int[][] dp =new int[prices.length][4];dp[0][0] = -prices[0];dp[0][1] = 0;dp[0][2] = 0;dp[0][3] = 0;for(int i = 1;i < prices.length;i++){dp[i][0] = Math.max(dp[i-1][0],Math.max(dp[i-1][3] - prices[i],dp[i-1][1]-prices[i]));dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);dp[i][2] = dp[i-1][0]+prices[i];dp[i][3] = dp[i-1][2];}return Math.max(dp[prices.length - 1][1],Math.max(dp[prices.length - 1][2],dp[prices.length - 1][3]));}
}二、714.买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ;非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
示例 1:
- 输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
- 输出: 8
解释: 能够达到的最大利润:
- 在此处买入 prices[0] = 1
- 在此处卖出 prices[3] = 8
- 在此处买入 prices[4] = 4
- 在此处卖出 prices[5] = 9
- 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:
- 0 < prices.length <= 50000.
- 0 < prices[i] < 50000.
- 0 <= fee < 50000.
思路
与买卖股票的最佳时机||类似,本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的。
dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
所以:dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金,注意这里需要有手续费了即:dp[i - 1][0] + prices[i] - fee
所以:dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
class Solution {public int maxProfit(int[] prices, int fee) {int len = prices.length;// 0 : 持股(买入)// 1 : 不持股(售出)// dp 定义第i天持股/不持股 所得最多现金int[][] dp = new int[len][2];dp[0][0] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = Math.max(dp[i - 1][0] + prices[i] - fee, dp[i - 1][1]);}return Math.max(dp[len - 1][0], dp[len - 1][1]);}
}这篇关于代码随想录算法训练营第五十天||309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




