出题123

本文主要是介绍出题123，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目时限空间说明

无特殊均默认$1s,256MB$

---

Problem a 最大化

• 在最大化目标值的基础上选择的操作越多越好，且输出操作应当按照顺序执行，即你的输出顺序就是你的执行顺序，当有多个执行顺序可以最大化目标值时，输出以编号为字典序较小的那个。

输入格式

第一行包含三个整数，$k,n,m(1\le k\le 10^5$，$0\le m\le n\le 10^5$)

第二行$k$个整数，表示$a_{\mathrm{1..}k}$（$1\le a_i\le n$）

接下来$n$行每行三个整数$t_j,i_j,b_j$，(1$\le t_j\le 3$，$1\le i_j\le k$，$1\le b_j\le 10^6$.

输出格式

第一行一个整数$k$，表示你选择的$k$个操作

后面$k$个整数，表示对应标号

样例输入

2 4 3
13 20
1 1 14
1 2 30
2 1 6
3 2 2

样例输出

3
2 3 4

样例解释

即执行$2,3,4$标号的操作，容易证明这样可以得到最大值.

---

Problem b 偶数

• 给定一个数组$a_n$，求解有多少个区间$[l,r]$满足其中$a[l..r]$中出现过的数都是出现偶数次。

输入格式

第一行一个整数$n$，$1\le n\le 10^5$
第二行$n$个整数，$a_i\in 2^m,0\le m\le 20$

输出格式

仅一行一个数，表示你要求的答案。

输入样例

4
1 1 2 2

输出样例

3

样例解释

答案是3，有三个区间满足其间每个数都出现了偶数次，即$[1,2],[3,4],[1,4]$

---

Problem c 唯一解

• 假设有一个排列$a_n$，再给定一个序列$b_n$，$b_i$的值为$j\in [1,i-1]$中满足$a_j<a_i$且$a_j$最大的对应位置$j$，若不存在这样的$j$，则$b_i=0$

• 现在给定序列$b_n$，要你求排列$a_n$

• 排列的定义：$a_i\in [1,n]$，且任意$i\ne j$，有$a_i\ne a_j$

• 数据保证存在唯一解

输入格式

输入第一行一个整数$1\le n\le 10^5$
第二行$n$个整数，表示序列$b_n，0\le b_i\le n$

输出格式

仅一行$n$个数，表示你要求的排列$a_n$。

样例输入

5
0 0 0 0 2

样例输出

5 3 2 1 4

数据规模与约定

因为在前$4$个数中只有$a_{2,3,4}<a_5$，且$a_2$最大，故$b_5=2$
容易证明这是唯一解。

---

problem d 远古程序 (6s,256mb)

题目描述

考古学家在 Alutila Cave 的深层发现了令人兴奋的泥板。没有人能够破译泥板上的文字，除了似乎描述了嵌套结构的两个符号，这两个符号与 LISP 中的左右括号有点类似。会不会是人类在几千年前就写了程序？

综合来看，这些泥板似乎描述了一部伟大的作品------也许是一段程序，或者是一部史诗，甚至是税收记录！不足为奇的是，经过这么长的时间，这些泥板都处于无序状态。你的工作是将它们排成一个序列，使产生的序列有一个合法的括号序列。只考虑到左括号和右括号，一个合法的括号序列是：

• $()$，或者
• $(A)$，其中 $A$ 是合法的括号序列，或者
• $AB$，其中 $A,B$ 都是合法的括号序列。

输入格式

输入第一行包含一个整数 $n(1\le n\le 10^6)$，表示泥板个数。接下来 $n$ 行，每行描述一个泥板。每行包含一个非空且由左右括号组成的字符串；与括号序列无关的符号在输入中被省略。字符串按出现在输入的顺序从 1 到 $n$ 编号。输入中最多有 $10^7$ 个括号。

输出格式

输出一个 1 到 $n$ 的排列，满足按这个顺序连接字符串就可以得到一个合法的括号序列。如果多个排列均可以满足条件，输出其中一个即可。如果没有满足要求的排列，输出 impossible。

样例输入1

2
())())()
((()

样例输出1

2
1

样例输入2

5
(
))
((
))
(

样例输出2

1
5
3
2
4

样例输入3

2
((
)

样例输出3

impossible

---

problem e 分流 (3s,256mb)

题目描述

分流系统是一个由节点组成的无环网络，它可以处理有限的数字序列。有两种类型的节点（如图 J.1）：

• 一个分流节点以一个数字序列作为输入，然后将它们交替分配到两个输出。第一个数字分流到输出 1，第二个分流到输出 2，第三个分流到输出 1，第四个分流到输出 2，以此类推。
• 一个汇聚节点以两个数字序列作为输入，并将它们交替合并，形成单一输出。首先输出输入 1 的第一个数字，然后是输入 2 的第一个数字，然后是输入 1 的第二个数字，然后是输入 2 的第二个数字，以此类推。如果其中一个输入序列比另一个短，那么在较短的序列用完后，较长序列中的剩余数字将被直接传送到输出，而不进行合并。

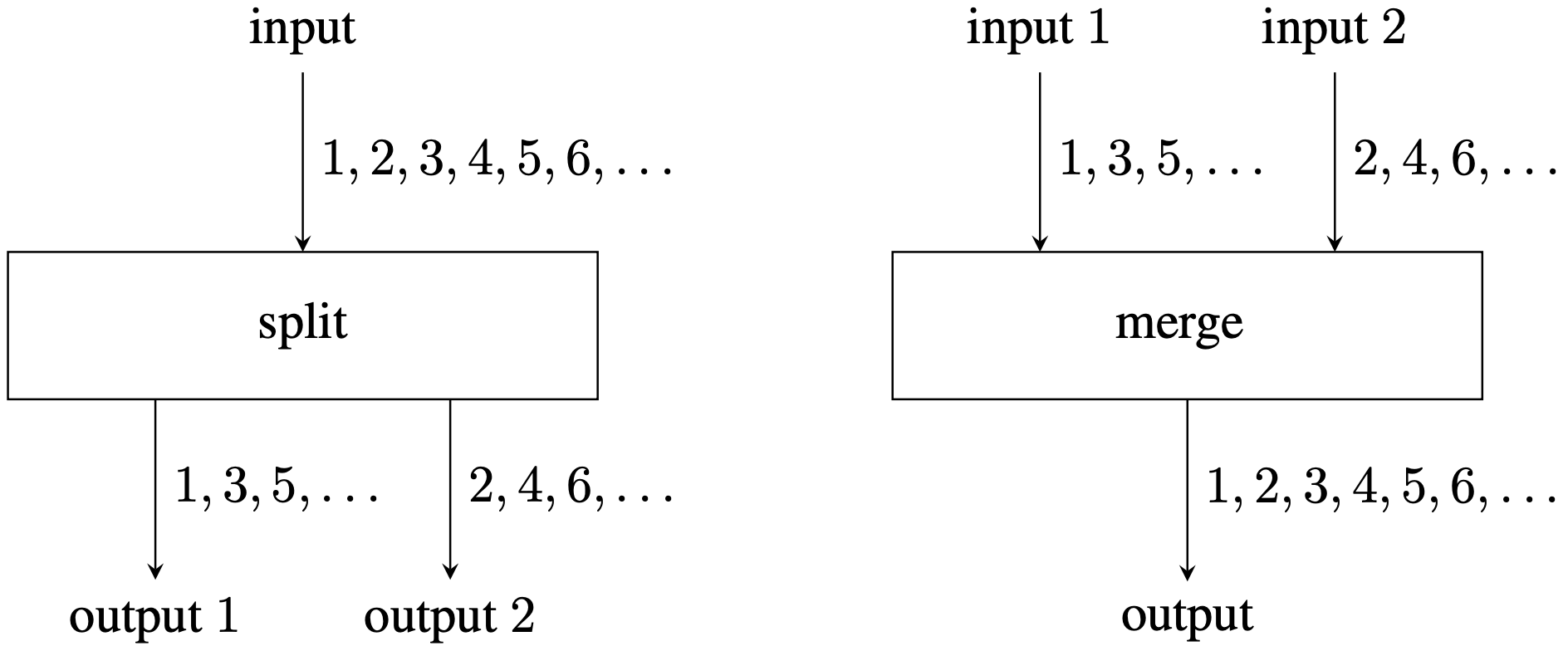
整个网络只有一个输入，是正整数序列 $1,2,3,\cdots ,m$。任何节点的输出都是可查询的。一个查询将会给定一个 $k$，确定一个节点输出的第 $k$ 个数是什么。你的任务是高效地实现这个查询功能。

输入格式

第一行包含三个整数 $m,n,q$，其中 $m(1\le m\le 10^9)$ 是输入序列的长度，$n(1\le n\le 10^4)$ 是节点个数，$q(1\le q\le 10^3)$ 是查询个数。

接下来 $n$ 行描述这个网络，每行描述一个节点。一个分流节点用 $\text{S}xyz$ 的格式描述，其中 $x,y,z$ 分别指定了这个节点的输入，第一个输出和第二个输出。一个汇聚节点用 $\text{M}xyz$ 的格式描述，其中 $x,y,z$ 分别指定了这个节点的第一个输入，第二个输入和输出。$x,y,z$ 是互不相同的正整数。总输入用 1 表示，剩余的输入/输出用从 2 开始的连续整数表示，除 1 以外的输入作为输出出现恰好一次。任意输出作为输入出现最多一次。

接下来 $q$ 行描述查询。每个查询包含两个整数 $x$ 和 $k$，其中 $x(2\le x\le 10^5)$ 是一个有效的输出，$k(1\le k\le 10^9)$ 是想要查询这个输出的第 $k$ 个数。序列的下标从 1 开始。

输出格式

对于每个询问输出一行，表示这个输出的第 $k$ 个数。如果没有下标为 $k$ 的数，输出 none。

样例输入1

200 2 2
S 1 2 3
M 3 2 4
4 99
4 100

样例输出1

100
99

样例输入2

100 3 6
S 1 4 2
S 2 3 5
M 3 4 6
6 48
6 49
6 50
6 51
6 52
5 25

样例输出2

47
98
49
51
53
100

样例输入3

2 3 3
S 1 2 3
S 3 4 5
M 5 2 6
3 1
5 1
6 2

样例输出3

2
none
none

---

Problem f 蠕虫

题目背景

地面上，一条蠕虫正在向面包屑艰难的爬行。

题目描述

地图是一个$n\ast m$的平面，蠕虫匍匐在地图上，它的基本移动方式和贪吃蛇一样，可以上下左右摆头，但不能撞到自己（不包括头撞尾）为了简化数据，我们把地图分四类：‘.’ ‘#’ ‘$@$’ '$1-9$’分别表示平地，障碍物，客厅，和蠕虫各节的编号（$1$是头，蠕虫至多长$9$格）。
现在，蠕虫想知道它要多久才能吃到面包屑（设定蠕虫每走一格耗时为$1$）。

现在我们着重介绍一下蠕虫的翻越（翻墙翻空地都可以）功能：
翻越有三个方向（不能倒着翻）选择，它可以翻越距离为$1$格的障碍物并前进沙虫长度数量的空地（或者单独前进沙虫长度数量+1的空地），翻越后每一节方向设为翻越方向，翻越时请无视身体带来的阻碍,耗时为$1$（详见样例）。

输入格式

先输入n和m,接下来2到$n+1$行，每行$m$个数，表示地图，$1<n,m<=15$

输出格式

蠕虫最短到@的时间$t$,若不能则输出$-1$（保证$@$只有一个）

样例输入

样例输入 #1

4 5
##...
..1#@
432#.
...#.

样例输出 #1

4

样例输入 #2

4 4
#78#
.612
.543
..@.

样例输出 #2

6

样例输入 #3

3 2
3@
2#
1#

样例输出 #3

-1

样例输入 #4

5 3
..@
...
...
###
321

---

Problem g 循环移位

题目描述

给定长度为 $2^n$ 的数组 $a_i$ ($0\le i<2^n$)，你可以进行任意次循环移位。

求 ${\sum }_{i=0}^{2^n-1}{a}_i\oplus i$， ${\sum }_{i=0}^{2^n-1}{a}_i\&i$，${\sum }_{i=0}^{2^n-1}{a}_i|i$ 的最大值。其中 $\oplus ,\&,|$ 分别代表按位异或，按位与，按位或。

对于一个长度为 $m$ 的数组 $x_i$ ($0\le i<m$)，其进行循环移位的结果 $x_i^{\prime }$ 为:

$$x_i^{\prime }=\{\begin{array}{ll}{x}_{i-1}& i\ne 0\\ x_{m-1}& i=0\end{array}$$

输入格式

输入第一行包含一个整数 $n$ ($1\le n\le 20$)，含义如题意所述。

接下来一行包含 $2^n$ 个整数 $a_i$ ($0\le a_i<2^n$)，为给定的数组。

输出格式

输出一行三个整数，由空格隔开，为 ${\sum }_{i=0}^{2^n-1}{a}_i\oplus i$，${\sum }_{i=0}^{2^n-1}{a}_i\&i$，${\sum }_{i=0}^{2^n-1}{a}_i|i$ 的最大值。

样例 #1

样例输入 #1

2
1 3 2 2

样例输出 #1

8 5 11

样例 #2

样例输入 #2

4
1 1 4 5 1 4 1 9 1 9 8 1 0 0 0 0

样例输出 #2

149 41 157

---

Problem h 最后一块石头的重量

题目描述

有一堆石头，用整数数组 $a$ 表示。其中 $a_i$ 表示第 $i$ 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 $x$ 和 $y$，且 $x\le y$。那么粉碎的可能结果如下：

• 如果 $x=y$，那么两块石头都会被完全粉碎；
• 如果 $x\ne y$，那么重量为 $x$ 的石头将会完全粉碎，而重量为 $y$ 的石头新重量为 $y-x$。

最后，最多只会剩下一块石头。输出此石头最小的可能重量。如果没有石头剩下，就输出 $0$。

输入格式

输入数据共两行。

第一行输入一个整数 $n$ ($1\le n\le 10000$)，表示石子的数量；

第二行输入 $n$ 个整数 $a_i$ ($1\le a_i\le 5000$)，表示第 $i$ 块石头的重量。

输出格式

输出数据共一行。

第一行输出一个整数表示答案。

样例 #1

样例输入 #1

6
2 7 4 1 8 1

样例输出 #1

1

样例 #2

样例输入 #2

5
31 26 33 21 40

样例输出 #2

5

---

Probelm i 太空港口

题目描述

有$M$个港口，从$1$到$M$编号，每个港口有等级$L_i$和点数$P_i$，每个港口每天生产利润量为$A\cdot L_i^2+B\cdot P_i+C$。

对于等级为$x$的港口，任意时刻，当它的点数$P_i$大于等于$x+1$时，立刻消耗$x+1$个点数，升级到第$x+1$个等级。

所有港口初始的等级$L_i$​、点数$P_i$​都为$0$。

小A在第$y$天开始时，会首先选择所有编号是$y$的因子的港口提升一点点数，即$\forall d|y,P_d:=P_d+1$，再生产利润，例如小A在第$1$天提升第$1$个港口，第$2$天提升第$1,2$个港口，第$3$天提升第$1,3$个港口，第$4$天提升第$1,2,4$个港口。

假如港口在每天升级完成后才会生产利润，智乃想知道第$1$天到第$N$天所有港口生产利润的总和是多少，请输出答案对$10^9+9$取余数后的结果。

输入描述:

仅一行五个正整数$N,M,A,B,C(1\le N,M\le 10^{12},1\le A,B,C\le 10^9)$

输出描述:

仅一行一个非负整数，表示问题的答案。

输入

3 5 10 1 1

输出

106

---

齿轮狩猎

题目描述

小Y的技能是一组联动齿轮，一共有$n$ 个齿轮，第$i$个齿轮的齿数为$a_i$，第$i$个齿轮的第 $j$ 个齿的攻击值为$b_{i,j}$。

每个齿轮上均拥有一个指针，第$0$ 秒时，每个齿轮均指向该齿轮的第 $1$ 个齿。

我们采用数字 $p_i$​ 代表第 iii 个齿轮指向的齿轮的编号，即一开始 $p_i=1$，$i\in [1,n]$。

当时间开始流逝，经过 $1$ 秒，第 $1$ 个齿轮转动一次，即 $p_1:=p_1+1$。

当第 $i$个齿轮旋转一圈后，第$i+1$个齿轮才转动一次，即每当 $p_i=a_i+1$时，$p_i:=1$，且 $p_{i+1}:=p_{i+1}+1$。

对于任意时刻，小Y的技能齿轮能产生的伤害为 ${\sum }_{i=1}^n{b}_{i,p_i}$。

现在小Y想要狩猎怪物，她已经获得了 $q$ 只怪物的信息，准备逐一狩猎这些怪物，对于第 $i$ 只怪物的血量为 HiH_iHi​，已知该怪物外出的时间段为 $[L_i,R_i]$。现在小Y想要一击必杀怪物，即$H_i\le {\sum }_{i=1}^n{b}_{i,p_i}$。请问小Y至少需要等待至多少秒，才能达成一击必杀的成就。

注意，每只怪物能否击杀均为独立询问

输入描述:

第一行给定两个整数 $n$ ，$q$，代表联动齿轮的个数，怪物的个数。

随后 $n$ 行数字代表第 iii 个齿轮的信息。

对于每一行，首先输入一个整数 $a_i$，代表第 iii 个齿轮的齿数，随后 $a_i$ 个整数 $b_{i,j}$ 代表第 $i$ 个齿轮的第 $j$个齿的攻击值。

随后 $q$ 行，每行三个数字 $H_i$，$L_i$，$R_i$​ ，分别代表怪物的血量、怪物出现时间、怪物消失的时间。

数据保证 $1\le n\le 100，1\le q\le 10^5，1\le a_i\le 50，1\le b_{i,j}\le 10^9，0\le L_i\le R_i<\min (10^{18},{\prod }_{i=1}^n{a}_i)，1\le H_i\le 10^9$。

输出描述:

输出 $q$ 行，每行输出一个整数代表答案，如果无法杀死怪物，请输出 $-1$。

输入

2 3
4 1 2 3 4
2 2 5
7 3 7
3 3 5
9 3 5

输出

5
3
-1

这篇关于出题123的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---