本文主要是介绍第123期 | 其他随机型存储模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
通过上期学习,大家已经了解了单周期的随机型存储模型,包括需求是离散随机变量的模型六以及需求是连续的随机变量的模型七。
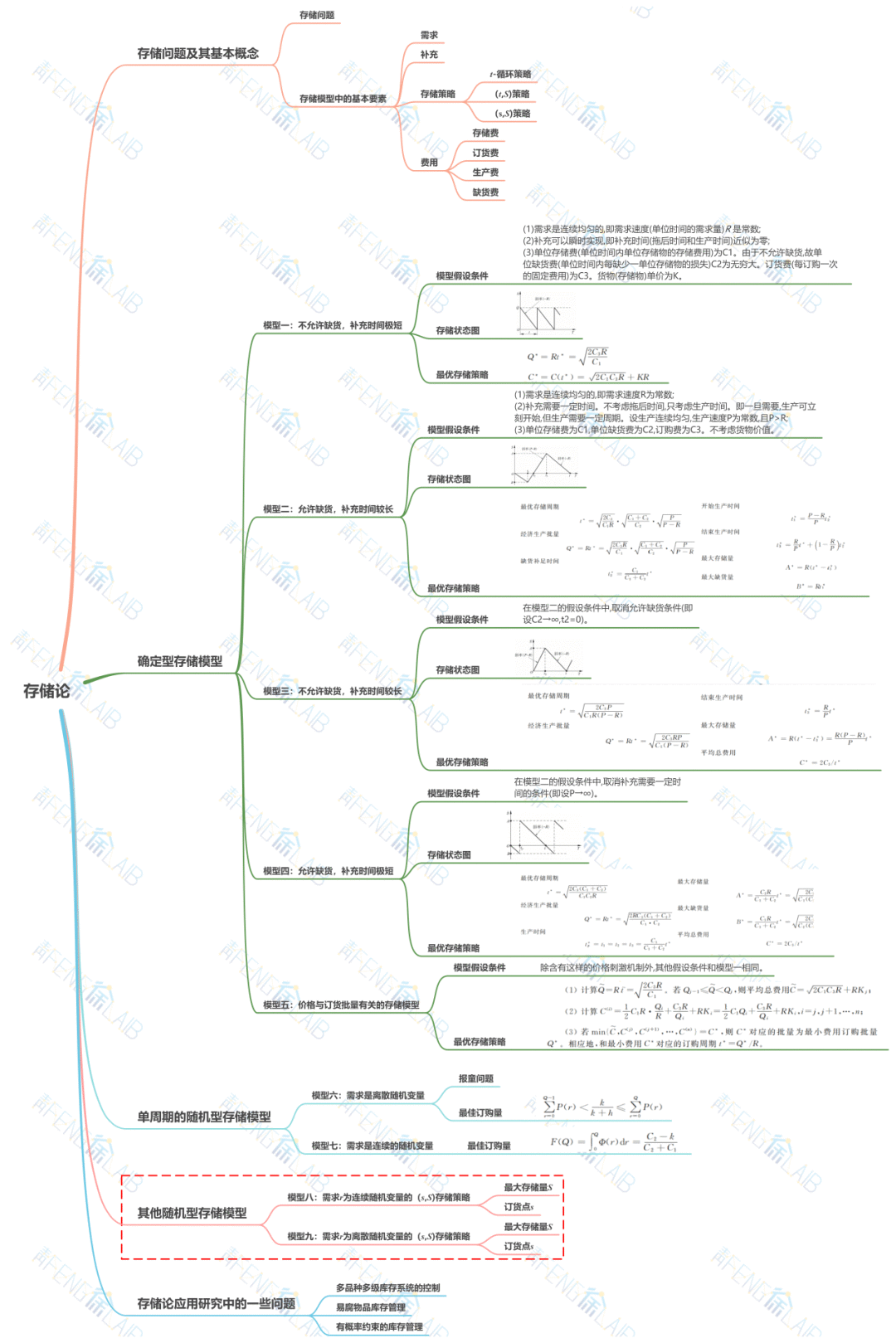
那么本期小编将为大家介绍其他随机型存储模型,包括需求r为连续随机变量的(s,S)存储策略的模型八和需求r为离散随机变量的(s,S)存储策略的模型九。
引言
货物单位成本为k、单位存储费为C1、单位缺货费为C2、每次订购费为C3、期初存储为I。需求r的概率分布已知。采用存储策略(s,S)(s为订货点、S为最大存储量)。问每次订货量Q如何确定,才能使损失期望值最小?
模型八:需求为r连续随机变量的(s,S)存储策略
需求r为连续随机变量,密度函数为

且
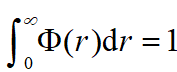
分布函数为
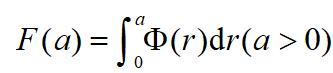
首先考虑最大存储量S。
当期初存储不足订货点(即I<S)时,需要订货,订货量Q=S-I。
和模型七类似,本阶段的损失期望值:
(期望损失值=订购费+货物成本+存储费+缺货费)
使期望损失值达到最小,即求上式的最小值,解
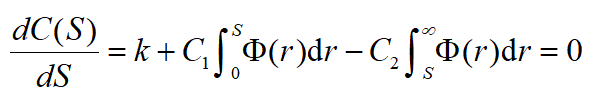
得

由于缺货损失至少包括失去销售机会的损失,而售价又高于成本,所以一般有
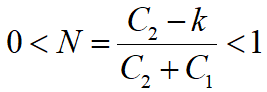
易证明,满足
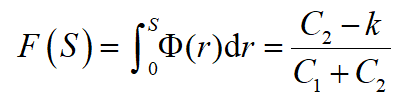
的S*是C(S)的最小点。且S*的确定和订货点s无关。
再考虑订货点s。
此时,最大存储量S*已经确定,根据s,当期初存储I=s时,不订货所造成的损失期望值应当不超过订货所造成的损失期望值。因此有
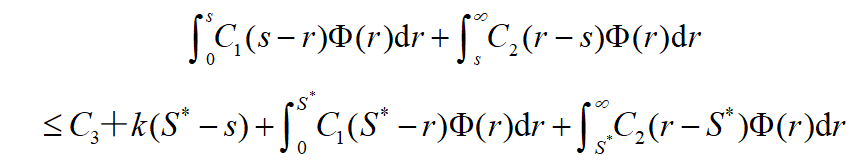
即
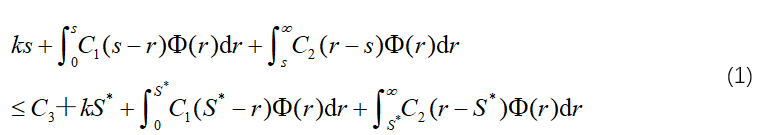
当s=S*时,上式显然成立,但问题的目的是要选取一个使上式成立的尽可能小的s值。
分析上式左边各项随s变化而变化的特点,比S*小的s是可能存在的。设使上式成立的最小的s为s*,则s*为(s,S)存储策略中的订货点s。
例题展示
石油公司经销某种燃料油。已知该燃料油每月销售量r(kg)服从指数分布。密度函数
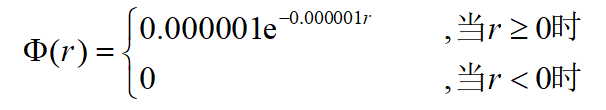
该燃料进价k=1.40元/kg,不需考虑订购费和存储费,即C1=0和C3=0。当缺货时需从其他石油公司购进,市场价为1.60元/kg。试定制(s,S)存储策略。
解:
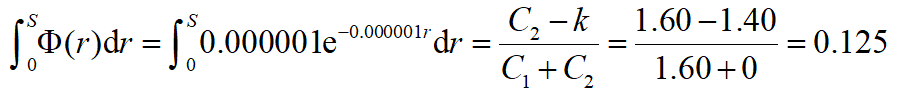
解之,得S*=133500,
因C1=C3=0,C2=1.6,S*=133500,所以
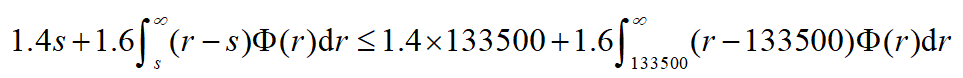
上式有唯一解s*=S*=133500。因此石油公司对该种燃料油应采取(s,S)=(133500,133500)的存储策略,即当库存燃料油减少到133500kg时,应订购,使库存重新达到133500kg。
模型九:需求为r散随机变量的(s,S)存储策略
需求r为离散随机变量。r=ri的概率P(ri)已知,
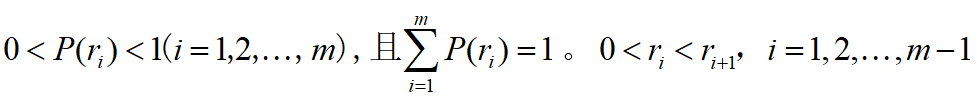
由于r是离散取值,订货点s和最大存储量S值只在r1,r2,...,rm中取,当S=ri时,记S=Si,即Si=ri(i=1,2,...,m)
除了需求为离散随机变量外,模型九和模型八的其他条件都相同。因此,两个模型的存储策略的制定过程基本原理是相同的。
下面直接给出模型九用于计算最大存储量S*和订货点s*的公式。
最大存储量S*计算公式:
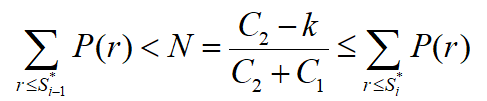
订货点s*计算公式:
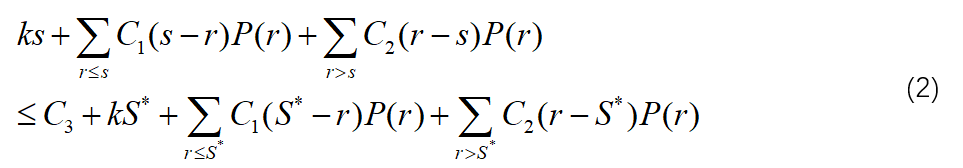
模型八和模型九采用(s,S)存储策略,当期初存储I≥s时,本阶段不订货;当I<s时,本阶段订货,订货量Q=S-I,即补足最大存储量S。
在实际使用这种存储策略时,如存储不易清点,因而实际存储量很难随时得知时,可将存储分两堆存放。一堆数量为s,其余的另放一堆。平时从后一堆取货以满足需求。当后一堆取完,需要动用前一堆时,期末就订货;如至期末,前一堆仍未动用,则本阶段不订货。因此,这种存储策略俗称双堆法(或两堆法)。
例题展示
商店销售某种商品。每月销售量r(件)为离散随机变量,其概率为
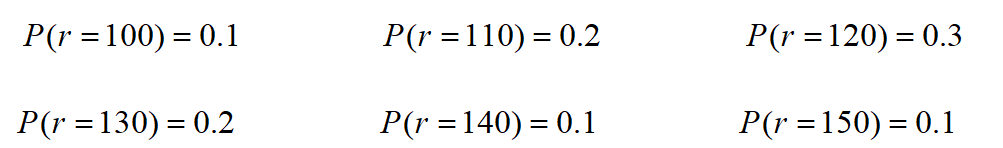
订货费C3=100元,每件商品进货成本k=500元。一个月中,每件商品存储费C1=10元,缺货费C2=800元,求(s,S)存储策略。
解:
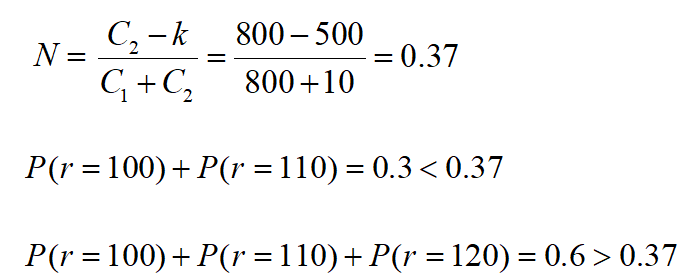
所以,S*=120件。
因为s≤S*,所以s从100,110,120中选择,且尽可能小,对于式(2),不等式右侧=65740。所以

故,s*=120件。
因此,商店对该商品应采取(s,S)=(120,120)的存储策略。
总结
通过例题可以看出,直接从式(1)和式(2)中解出订货点s*是十分困难的。
但是,对于实际问题,当最大存储量S*确定后,只要记住订货点s*的三个性质,在数值上确定s*是不困难的。
s*的三个性质是:
(1)s*≤S*;
(2)s*满足式(1)或式(2);
(3)s*是所有满足式(1)或式(2)的s中最小的。
因此,对于需求是连续随机变量的情况,可以在问题允许的精度上,将区间[0,S*]进行n等分。设等分点依次为d0(=0),d1,...,dn(=S*),然后将各等分点依次逐个代入式(1)检验,首先满足式(1)的
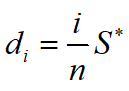
,即为订货点s*。
对于需求是离散随机变量的情况,可以按r1,r2,...,rj=S*的顺序,逐个代入式(2)中检验,首先满足式(2)的
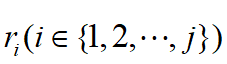
即为订货点s*;
当然,无论两种情况中的哪一种,在逐个检验前,如能根据已知数据将式(1)或式(2)尽可能地化简(得出关系式右边和订货点s无关),有利于减少检验时的计算量。
以上就是其他随机型存储模型的全部内容了,下一期小编将为大家介绍存储论应用研究中的一些问题,敬请关注!
作者 | 唐京茹 李超凡
责编 | 唐京茹
审核 | 徐小峰
这篇关于第123期 | 其他随机型存储模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





