黄明游专题
【数值计算方法(黄明游)】数值积分(一):复化(梯形公式、中点公式)【理论到程序】
文章目录 一、梯形公式、中点公式1. 梯形公式(Trapezoidal Rule):2. 复化梯形公式(Composite Trapezoidal Rule):3. 中点公式(Midpoint Rule):4. 复化中点公式(Composite Midpoint Rule): 二、例题三、程序1. 中点公式2. 梯形公式 积分学的基本定理告诉我们,只要能找到 f ( x
【数值计算方法(黄明游)】函数插值与曲线拟合(二):三次 Hermite 插值【理论到程序】
文章目录 一、近似表达方式1. 插值(Interpolation)2. 拟合(Fitting)3. 投影(Projection) 二、Lagrange插值1. 拉格朗日插值方法2. Lagrange插值公式a. 线性插值(n=1)b. 抛物插值(n=2) 三、Newton插值四、三次 Hermite 插值1. 天书2. 人话3. 例题4. python实现 一、近似表达方式
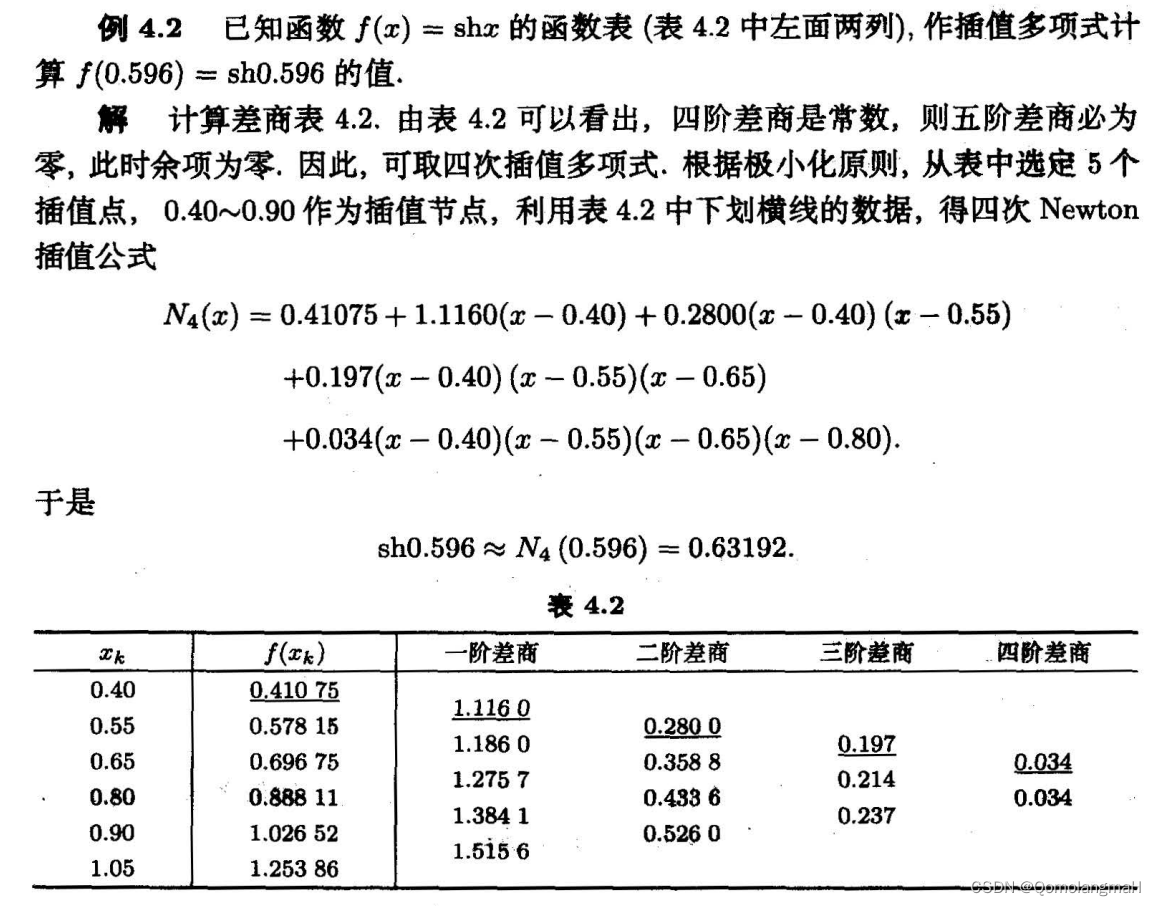
【数值计算方法(黄明游)】函数插值与曲线拟合(二):Newton插值【理论到程序】
文章目录 一、近似表达方式1. 插值(Interpolation)2. 拟合(Fitting)3. 投影(Projection) 二、Lagrange插值1. 拉格朗日插值方法2. Lagrange插值公式a. 线性插值(n=1)b. 抛物插值(n=2) 三、Newton插值1. 天书2. 人话3. 例题4. python实现5. C语言实现 一、近似表达方式 插值、
【数值计算方法(黄明游)】函数插值与曲线拟合(一):Lagrange插值【理论到程序】
文章目录 一、近似表达方式1. 插值(Interpolation)2. 拟合(Fitting)3. 投影(Projection) 二、Lagrange插值1. 天书2. 人话拉格朗日插值方法a. 线性插值(n=1)基本思想线性插值与线性方程组 b. 抛物插值(n=2)基本思想优点和局限性应用场景 c. n次插值基本思想插值基函数的选择优点和和局限性 3. python实现4. C语言实
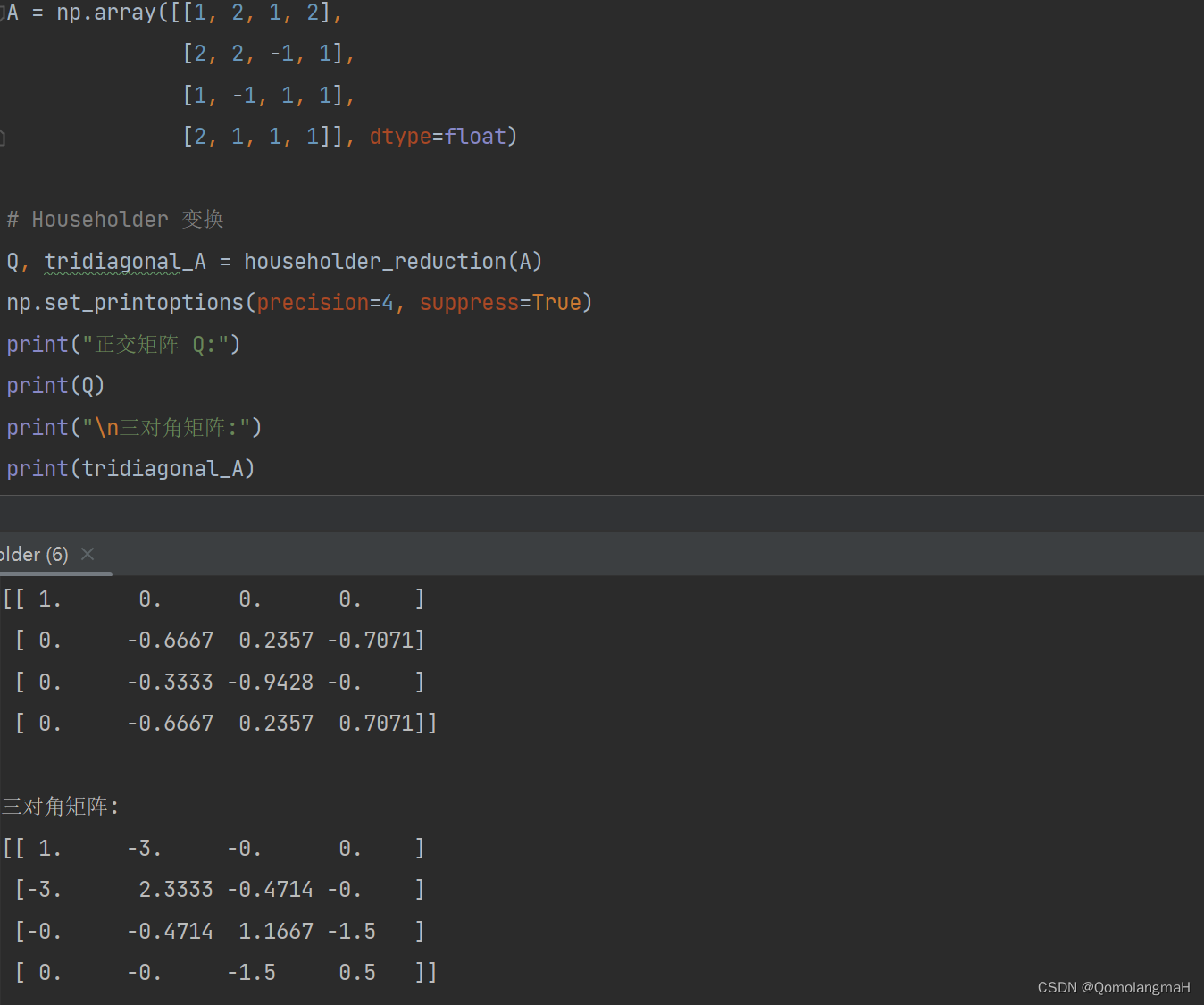
【数值计算方法(黄明游)】矩阵特征值与特征向量的计算(五):Householder方法【理论到程序】
文章目录 一、Jacobi 旋转法二、Jacobi 过关法三、Householder 方法1. 旋转变换a. 旋转变换的选择b. 旋转变换的顺序 2. Householder矩阵(Householder Matrix)a. H矩阵的定义b. H变换的几何解释c. H变换的应用场景 3. H变换过程详解a. 过程介绍b. 细节解析 4. H变换例题解析 四、Python实现调试过程
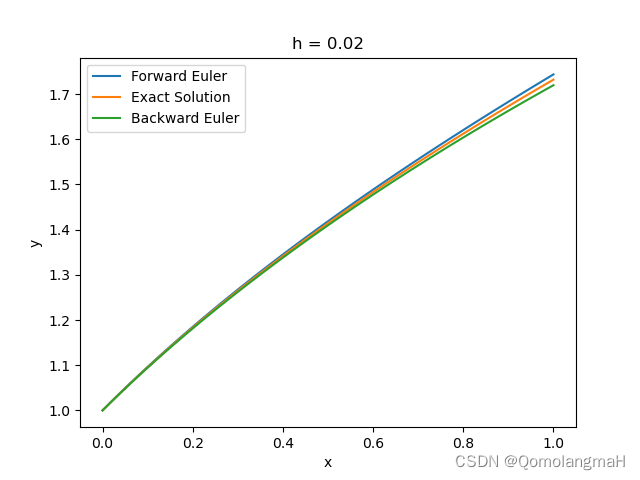
【数值计算方法(黄明游)】常微分方程初值问题的数值积分法:欧拉方法(向后Euler)【理论到程序】
文章目录 一、数值积分法1. 一般步骤2. 数值方法 二、欧拉方法(Euler Method)1. 向前欧拉法(前向欧拉法)2. 向后欧拉法(后向欧拉法)a. 基本理论b. 算法实现 常微分方程初值问题的数值积分法是一种通过数值方法求解给定初始条件下的常微分方程(Ordinary Differential Equations, ODEs)的问题。 一、数值积分法
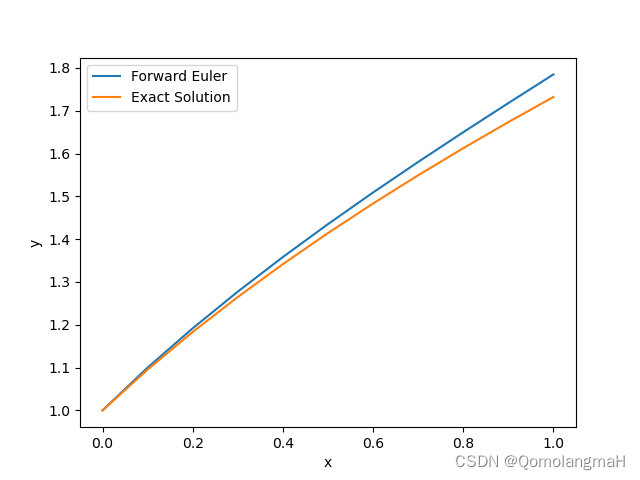
【数值计算方法(黄明游)】常微分方程初值问题的数值积分法:欧拉方法(向前Euler)【理论到程序】
文章目录 一、数值积分法1. 一般步骤2. 数值方法 二、欧拉方法(Euler Method)1. 向前欧拉法(前向欧拉法)a. 基本理论b. 典例解析c. 算法实现 常微分方程初值问题的数值积分法是一种通过数值方法求解给定初始条件下的常微分方程(Ordinary Differential Equations, ODEs)的问题。 一、数值积分法 1. 一般步骤