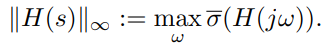复杂的µ合成问题成为一个具有特殊结构控制器的设计问题。 H无穷范数（H∞ norm）：对于线性时不变（LTI）系统，H∞范数通常定义为系统频率响应的最大幅值。换句话说，它是系统传递函数在复平面单位圆上的最大绝对值。最大奇异值：对于一个矩阵，其奇异值是该矩阵与其共轭转置矩阵乘积的特征值的平方根。对于方阵，这等同于特征值的绝对值。然而，对于系统传递函数的矩阵（例如，多输入多输出系统的传递

鲁棒控制（Robust Control）是一种控制系统设计方法，其目标是使控制系统在面临参数摄动、外部干扰、建模误差等不确定性因素时，仍能够保持其期望的性能特性。鲁棒性是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。 根据对性能的不同定义，鲁棒性可分为稳定鲁棒性和性能鲁棒性。稳定鲁棒性主要关注系统在面对不确定性时能否保持稳定，而性能鲁棒性则关注系统能否在不确定性影响下维持其性能

鲁棒性，即系统的健壮性，是指在异常和危险情况下系统能够维持其功能和性能的能力。在控制系统中，鲁棒性表现为系统在参数摄动下维持某些性能的特性。例如，当控制系统面临输入错误、磁盘故障、网络过载或有意攻击等挑战时，其能否保持稳定并继续有效运行，就体现了其鲁棒性。 状态反馈和前馈是提升系统鲁棒性的两种重要手段。状态反馈是将系统的状态信息作为反馈信号，通过反馈回路来调整系统的控制输入，以达到期望的控制目标

由于在构建Delta机构动力学模型的时候采取了一些假设（主动臂从动臂都认为是均质杆1）本次仿真采用关节空间鲁棒计算力矩控制的方法控制机器人。 1.1 计算力矩控制 常规的计算力矩控制策略如图 1所示，使用估计的机器人动力学模型控制实际的机器人，在理想的情况下，即估计所用的模型与实际模型完全一致： M ^ = M , n ^ = n \widehat{M} = M,\ \widehat{n} =

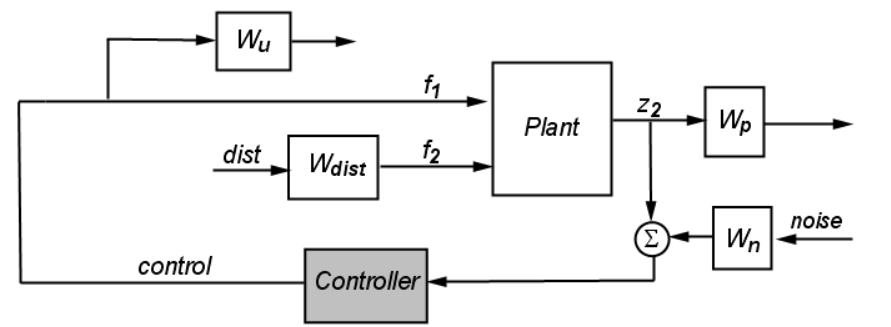
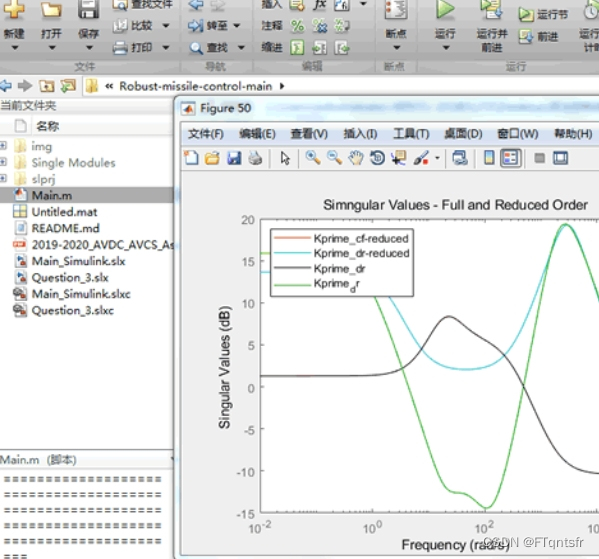
自主控制系统分配：包含一个MATLAB Simulink仿真，用于超音速导弹系统的飞行动态仿真和鲁棒控制 自主控制系统分配在导弹系统中扮演着至关重要的角色，可以有效地提高导弹系统的精度和可靠性。其中，MATLAB Simulink仿真是自主控制系统分配中的关键工具，可用于超音速导弹系统的飞行动态仿真和鲁棒控制。在本文中，我们将详细探讨自主控制系统分配的原理和实现，以及MATLAB Simulin