本文主要是介绍鲁棒控制问题描述,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
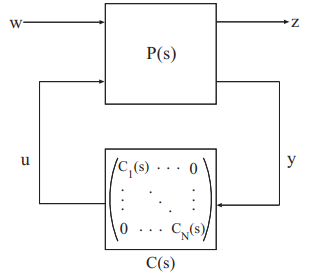
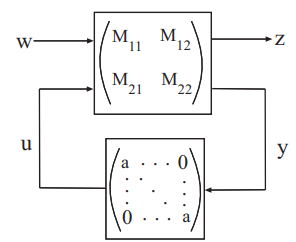
复杂的µ合成问题成为一个具有特殊结构控制器的设计问题。
![]()
- H无穷范数(H∞ norm):对于线性时不变(LTI)系统,H∞范数通常定义为系统频率响应的最大幅值。换句话说,它是系统传递函数在复平面单位圆上的最大绝对值。
- 最大奇异值:对于一个矩阵,其奇异值是该矩阵与其共轭转置矩阵乘积的特征值的平方根。对于方阵,这等同于特征值的绝对值。然而,对于系统传递函数的矩阵(例如,多输入多输出系统的传递函数矩阵),最大奇异值并不直接等同于H∞范数,除非该矩阵是方阵且仅考虑一个频率点。
- Bode图:Bode图是一种用于显示系统频率响应的图形表示,它显示了幅值增益和相位角随频率的变化。在Bode图中,最大的幅值增益对应于H∞范数,因为H∞范数就是系统在所有频率上的最大幅值增益。
- H无穷范数就是最大奇异值:这个说法是不准确的。H∞范数是系统在所有频率上的最大幅值增益,而最大奇异值通常用于描述矩阵的特性,并不直接等同于H∞范数。
- H无穷范数就是Bode图中最大的幅值增益:这个说法是正确的。H∞范数确实等于Bode图中显示的幅值增益的最大值。
在Bode图中,幅值增益曲线反映了系统对于不同频率输入信号的放大能力。由于H无穷范数定义为系统传递函数在所有频率上的最大幅值增益,因此它对应于Bode图中幅值增益曲线的最大值。换句话说,当我们观察Bode图时,可以通过找到幅值增益曲线的最高点来确定H无穷范数的值。
这篇关于鲁棒控制问题描述的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






