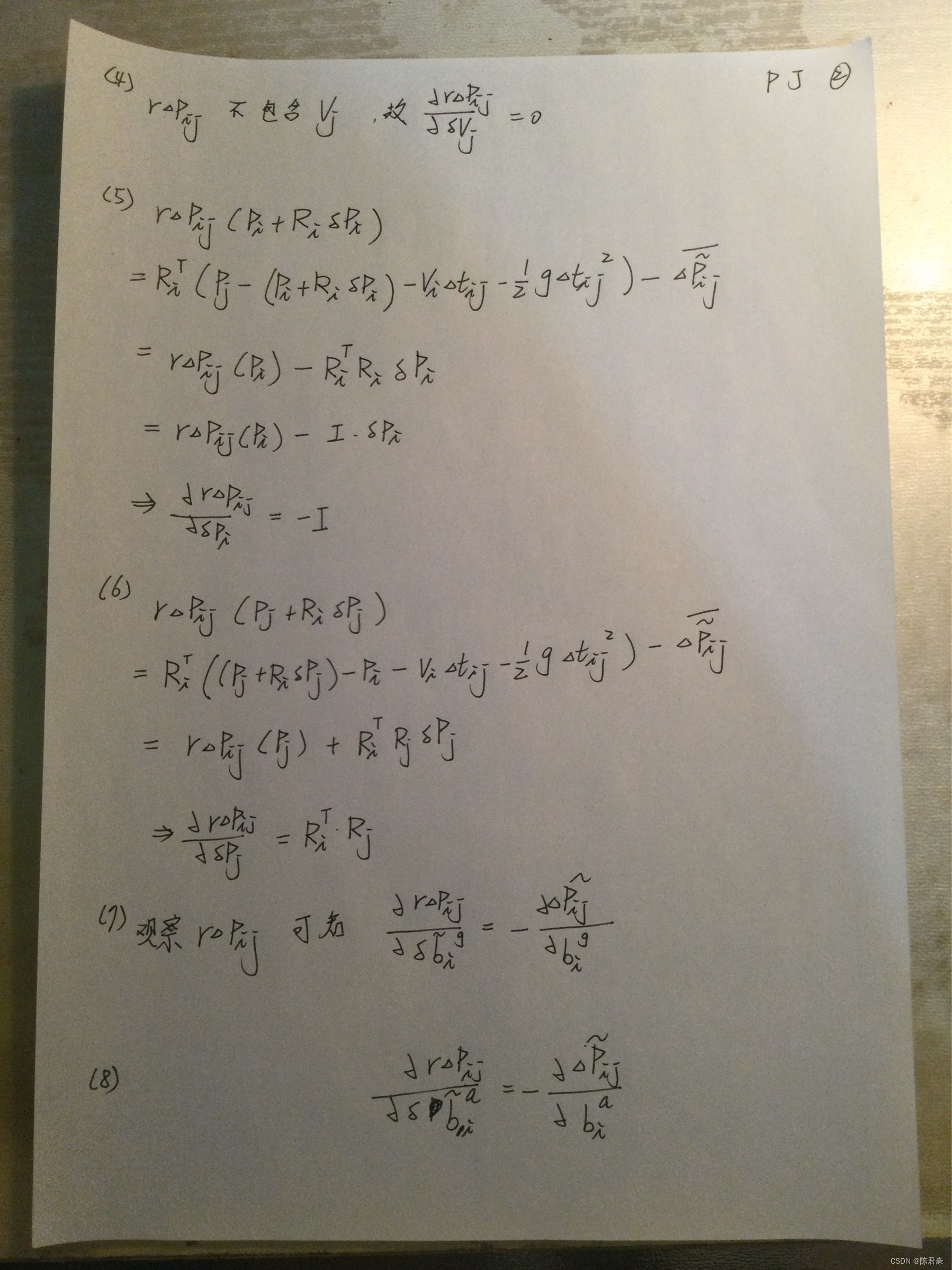矩阵的特征值和特征向量是线性代数以及矩阵论中非常重要的一个概念。在遥感领域也是经常用到，比如多光谱以及高光谱图像的主成分分析要求解波段间协方差矩阵或者相关系数矩阵的特征值和特征向量。 根据普通线性代数中的概念，特征值和特征向量可以用传统的方法求得，但是实际项目中一般都是用数值分析的方法来计算，这里介绍一下雅可比迭代法求解特征值和特征向量。 雅克比方法用于求实对称阵的全部特征值、特征向量。 对

雅可比矩阵是以一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。 雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此，雅可比矩阵类似于多元函数的导数。 海森矩阵是一个以自变量为向量的实值函数的二阶偏导数组成的方块矩阵。 此函数如下，f（x1,x2,...,xn）如果f的所有二阶导数都存在，那么f的海森矩阵即： 海森矩阵在牛顿

1. 常规雅克比矩阵的逆 根据关节角度，可得末端速度方程： v e = J ( q ) q ˙ v_e=J(q)\dot q ve​=J(q)q˙​ 如果雅克比矩阵式方阵且可逆，可得关节速度为 q ˙ = J − 1 ( q ) v e \dot q=J^{-1}(q)v_e q˙

文章目录 1. 手推机器学习-矩阵求导1.1 绪论1.2 ML中为什么需要矩阵求导1.3 向量函数与矩阵求导初印象1.4 矩阵求导-YX拉伸术1.5 常见矩阵求导公式举例1.6 求导细节补充 2. 雅克比矩阵2.1 雅克比矩阵数学2.2 雅克比矩阵pytorch2.3 向量对向量求导&矩阵对矩阵求导2.4 小结 1. 手推机器学习-矩阵求导 B站链接 1.1 绪论 （1）理