笛卡尔专题
拉普拉斯算子从笛卡尔坐标系到圆柱坐标系下的推导过程
这段时间推导圆膜振动方程的时候,需要将振动方程从笛卡尔坐标系转换到圆柱坐标系。虽然这个结果书上都有了,但是不满足于直接给出的结果,想自己推导一下。于是就有了下面的内容。总结起来:就是将笛卡尔坐标系下的拉普拉斯算子定义式和圆柱坐标系下拉普拉斯算子定义式之间的关系通过坐标转换对应起来,然后利用待定系数法求解相应的系数就可以了。话不多说,上干货。 笛卡尔坐标系下的拉普拉斯算子定义为: (2-1)
hive sql优化(全排序,笛卡尔积,exist in,决定reducer个数,合并MapReduce)
hive 全排序 优化 分类: hive hadoop hadoop 2013-01-28 20:11 717人阅读 评论(0) 收藏 举报 hive hadoop 目录(?)[+] 使用Hive可以高效而又快速地编写复杂的MapReduce查询逻辑。但是某些情况下,因为不熟悉数据特性,或没有遵循Hive的优化约定,Hive计算任务会变得非常低效,甚至无法得到结果。一个”好”的Hive程序
wpf livechart 绘制笛卡尔曲线
先上图: 代码部分: <GroupBox Header="各生产线生产量趋势"><Grid><Grid.RowDefinitions><RowDefinition Height="45"/><RowDefinition Height="auto"/><RowDefinition/></Grid.RowDefinitions><Border CornerRa
【面试干货】什么是内连接、外连接、交叉连结、笛卡尔积?
【面试干货】什么是内连接、外连接、交叉连结、笛卡尔积? 1、内连接(Inner Join)2、左外连接(Left Outer Join)3、右外连接(Right Outer Join)4、全外连接(Full Outer Join)5、交叉连接(Cross Join) 💖The Begin💖点点关注,收藏不迷路💖 在数据库查询中,连接(Join)是一种用于将两个
PHP 实现笛卡尔积
<?php$arr = array(array(1,3,4,5),array(3,5,7,9),array(76,6,1,0));/**** 实现二维数组的笛卡尔积组合** $arr 要进行笛卡尔积的二维数组** $str 最终实现的笛卡尔积组合,可不写** @return array**/function cartesian($arr,$str = array()){//去除第一
【退役之重学 SQL】什么是笛卡尔积
一、初识笛卡尔积 概念: 笛卡尔积是指在关系型数据库中,两个表进行 join 操作时,没有指定任何条件,导致生成的结果集,是两个表中所有行的组合。 简单来说: 笛卡尔积是两个表的乘积,结果集中的每一行都是第一个表的每一行与第二个表的每一行的组合。 注意事项: 在实际数据库的查询中,应尽量避免笛卡尔积的产生,因为它会导致结果集过大、性能下降,而且通常不是我们所期望的查询结果。因此在进行 join
Spark RDD 笛卡尔积
Spark RDD 笛卡尔积 val left = sc.parallelize(List(1,2,3))val right = sc.parallelize(List(3,4,5,6))val out = left union right //返回所有元素新的RDD //{1,2,3,3,3,4,5,6}val insterstions = left intersection
POJ 2201:Cartesian Tree ← 笛卡尔树模板题
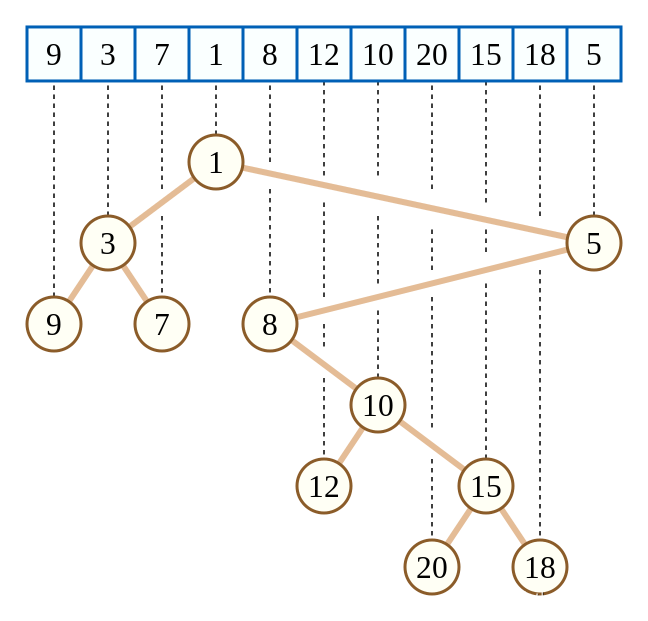
【题目来源】http://poj.org/problem?id=2201【题目描述】 Let us consider a special type of a binary search tree, called a cartesian tree. Recall that a binary search tree is a rooted ordered binary tree, such that
ROS Industrial 软件包_笛卡尔路径规划器_实现
笛卡尔(Descarte)路径规划 使用笛卡尔包 使用笛卡尔包需要软件开发人员创建三个对象Obiects: 一个机器人模型(a robot model),将用来计算正向运动学和逆向运动学。 一个轨迹点的轨迹(a trajectory of trajectory points),用于定义路径。 一个规划器(a planner),将使用提供的机器人模型来完成沿着轨迹寻找有效路线的工作。
ROS Industrial 软件包_笛卡尔路径规划器_介绍
笛卡尔(Descartes) 概要 笛卡尔(Descartes)是ROS-Industrial项目,用于对未定义的笛卡尔轨迹执行路径规划。 动机 当前的MoveIt / ROS接口专注于拾取pick和放置place应用。在典型的拾取和放置应用中,起始位置和目标位置是路径规划者的唯一输入。相比之下,许多工业应用必须遵循预定义的笛卡尔路径,不仅起始和结束位置很重要,而且两者之间的路径也很
ROS Industrial教程(七)_笛卡尔规划和执行2
加载参数 在本练习中,我们将加载一些ROS参数以初始化程序中的重要变量。 定位练习源文件 ·转到位于plan_and_run/src/plan_and_run_node.cpp中的主应用程序源文件。 ·在主程序中,找到对application.loadParameters()的函数调用。 ·转到位于plan_and_run/src/tasks/load_parameters.cpp中的该
ROS Industrial教程(七)_笛卡尔规划和执行1
笛卡尔规划和执行 引言 目标 接下来将介绍如何使用笛卡尔库中的各种组件来从半约束点轨迹规划和执行机器人路径。 包括: ·熟悉笛卡尔工作流程。 ·了解如何加载自定义的笛卡尔RobotModel。 ·了解如何从6DOF(Six degrees of freedom六自由度)工具姿势创建半约束轨迹。 ·使用笛卡尔规划器规划机器人路径。 ·将笛卡尔路径转换为MoveIt!消息以执行运动。
【MySql】MySQL查询中的笛卡尔积现象解析
还有多少个十年 能勇敢做热血青年 还有多少个十年 能坚持当初的信念 还有多少个十年 能不忘怀回忆点点 🎵 《还有多少个十年》 在使用MySQL或任何关系型数据库进行多表查询时,如果连接条件设置不当,就可能发生所谓的笛卡尔积现象。这通常会导致大量无用数据的生成,严重时甚至会拖慢整个数据库的性能。 什么是笛卡尔积? 笛卡尔积发生在多表查询时,当
2016 ICPC Hong Kong G Scaffolding —— 笛卡尔树上DP
This way 题意: 他这个题意稍微的不正确,它应该是放了这个竹子之后就到这个竹子上面(也许)。否则样例,题解和程序就不对了吧。 题解: 大致思路就是这样,我这里用dp代替了f,res代替了g。 sum表示子树的值的和,siz表示子树大小。 ll v=(a[x]-a[fa])*siz[x]-res[ls[x]]-res[rs[x]]; 表示当前点把统治的区间内的所有点的高拆到和父亲
POJ 2559 Largest Rectangle in a Histogram —— 笛卡尔树模板
This way 题意: 现在有n个连着的矩形,每个矩形的宽为1,高为a[i],问你在这些矩形内部最大能组成的矩形大小。 题解: 笛卡尔树模板,模板和之前有了一些变化,增加了连边的特判,这样子就算有起始点为0的地方也无妨。当然要注意初始化 #include<bits/stdc++.h>using namespace std;#define ll long longconst i
深入解析Oracle数据库中的笛卡尔积连接
在Oracle数据库中,笛卡尔积连接(也称为交叉连接,Cross Join)是指两个表之间没有指定任何连接条件时进行的连接操作。这种连接将第一个表中的每一行与第二个表中的每一行进行配对,生成的结果集包含了所有可能的行组合,其大小等于第一个表的行数乘以第二个表的行数。 例如,假设我们有两个表tableA和tableB,分别有m行和n行,那么执行笛卡尔积连接后将产生m * n行的结果: SELEC
Oracle笛卡尔积,分组,多表连接
一 oracle的单行函数 转换函数 to_date(日期字符串,日期格式) 字符串的格式必须由第二个参数来判断 日期格式 : 年 yyyy,月mm,日dd,小时(hh12小时制,hh24 24小时制) 分钟 mi 秒 ss
LOJ#6032. 「雅礼集训 2017 Day2」水箱【笛卡尔树】
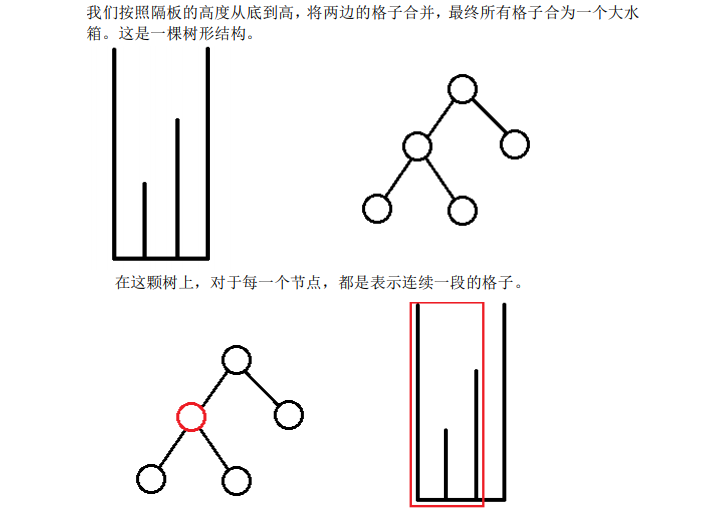
题目描述: 题目分析: 如果想象水慢慢往上涨,高的隔板会将不同的区域分隔开,导致两边的水位高低可能不一样。 而水位如果超过了隔板,那么这个隔板两边就等价了。 于是我们想到用最大值将区间划分,然后答案就可以这么求(设当前隔板的高度为h,最近的比当前隔板高的隔板的高度为h’): 如果水位没有达到当前隔板,可以满足的条件为h到h’中无水的条件加上当前隔板两边水位任意时最多满足的条件。 如果水位
018—pandas 生成笛卡尔积排列组合合并多列字符串数据
思路: 本需求需要将给定的几列数据,生成一个排列组合形式的数据列,利用到 Pandas 多层索引生成的笛卡尔积的方法。 二、使用步骤 1.引入库 代码如下(示例): import pandas as pd 2.读入数据 代码如下(示例): df = pd.DataFrame({'姓名': list('甲乙丙')+[None],'序号': list('12')+[None]*2,'
【MySQL】学习多表查询和笛卡尔积
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-N8PeTKG6uLu4bJuM {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-sv
【无标题】Matlab 之axes函数——创建笛卡尔坐标区
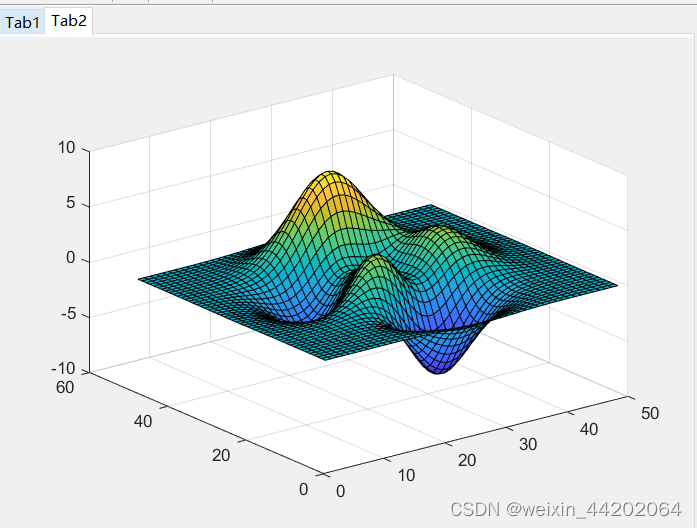
**基本用法:**axes 在当前图窗中创建默认的笛卡尔坐标区,并将其设置为当前坐标区。 应用场景1:在图窗中放置两个 Axes 对象,并为每个对象添加一个绘图。 要求1:指定第一个 Axes 对象的位置,使其左下角位于点 (0.1 0.1) 处,宽度和高度均为 0.7。指定第二个 Axes 对象的位置,使其左下角位于点 (0.65 0.65) 处,宽度和高度均为 0.28。默认情况下,所有值为
SQL INNER JOIN LEFT JOIN RIGHT JOIN 笛卡尔积
https://blog.csdn.net/Michaelwubo/article/details/80923248
pgsql隐式联查的笛卡尔积和子查询性能
语句: 1、select a.* from table_a a,table_b b where b.id in (‘1’,‘2’,‘3’) and a.con =b.con 2、select a.* from table_a where a.con in (select con from id in (‘1’,‘2’,‘3’)) 条件: 1、table_a表的con字段是索引,table_b
「JOISC 2020 Day3」星座 3 (DFS序)(笛卡尔树)(DP)
传送门 建出笛卡尔树,假设当前处理 [ l , r ] [l,r] [l,r],高于最大值的星星只能保留一个 一颗星星可以定位到上述的唯一一个区间,所以我们可以枚举这一棵星星 选了这颗星星的话会 b a n ban ban 掉一些区间的星星,而这个在笛卡尔树上是一条链 如果令 f , g f,g f,g 表示当前区间不选 / 选星星,那么 b a n ban ban 掉的就是强制不选星星
php 笛卡尔积的实现
<?php$arr = array(array(1,3,4,5),array(3,5,7,9),array(76,6,1,0));/**** 实现二维数组的笛卡尔积组合** $arr 要进行笛卡尔积的二维数组** $str 最终实现的笛卡尔积组合,可不写** @return array**/function cartesian($arr,$str = array()){//去除第一