LOJ#6032. 「雅礼集训 2017 Day2」水箱【笛卡尔树】

题目描述：

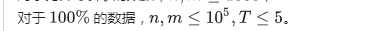
题目分析：

如果想象水慢慢往上涨，高的隔板会将不同的区域分隔开，导致两边的水位高低可能不一样。
而水位如果超过了隔板，那么这个隔板两边就等价了。
于是我们想到用最大值将区间划分，然后答案就可以这么求（设当前隔板的高度为h，最近的比当前隔板高的隔板的高度为h’）：
如果水位没有达到当前隔板，可以满足的条件为h到h’中无水的条件加上当前隔板两边水位任意时最多满足的条件。
如果水位达到了当前隔板，可以满足的条件为h到当前水位中有水的条件加上当前水位到h’中无水的条件加上隔板两边水满时能够满足的条件。

这样笛卡尔树的树形DP的模型就很容易看出来了。

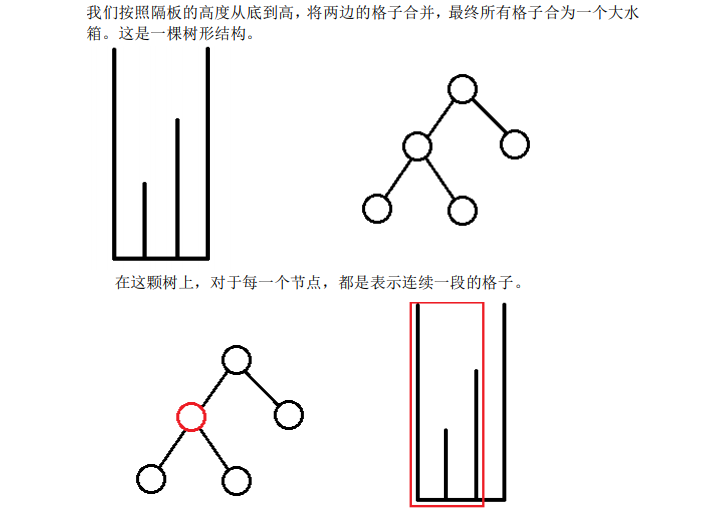
还有一个实现的细节就是怎么知道条件在笛卡尔树中哪一个点的管辖范围内。
可以尝试由小到大枚举隔板的高度，初始化L[i]=R[i]=i，将高度小于条件高度的隔板删去（令L[i]=i-1,R[i]=i+1），然后并查集查找到高度大于条件的最近的隔板，他在笛卡尔树上的左儿子或右儿子就是我们要找的点。
也可以尝试从条件的横坐标对应的笛卡尔树上的节点在树上倍增，找到最后一个高度<=条件的点即可。

Code：

#include<bits/stdc++.h>
#define maxn 200005
#define maxp maxn*17
#define maxm maxp*6
using namespace std;
char cb[1<<18],*cs,*ct;
#define getc() (cs==ct&&(ct=(cs=cb)+fread(cb,1,1<<18,stdin),cs==ct)?0:*cs++)
inline void read(int &a){char c;while(!isdigit(c=getc()));for(a=c-'0';isdigit(c=getc());a=a*10+c-'0');
}
const int Log = 16;
int n,m,tot,h[maxn],S[maxn],tp,f[maxn][Log+1],pos[maxn],dp[maxn][2];
int rt,lc[maxn],rc[maxn];
vector<pair<int,int> >G[maxn];
void dfs0(int &u,int ff){if(!u) tot++,pos[tot]=u=n+tot-1;//single point, middle implementation 1~nf[u][0]=ff;for(int i=1;i<=Log;i++) f[u][i]=f[f[u][i-1]][i-1];if(u<n) dfs0(lc[u],u),dfs0(rc[u],u);
}
void dfs(int u){if(!u) return;dfs(lc[u]),dfs(rc[u]);sort(G[u].begin(),G[u].end());int s0=0,s1=0;for(auto i:G[u]) if(!i.second) s0++;dp[u][0]=dp[lc[u]][0]+dp[rc[u]][0]+s0;for(auto i:G[u]){i.second?s1++:s0--;dp[u][0]=max(dp[u][0],dp[lc[u]][1]+dp[rc[u]][1]+s1+s0);}dp[u][1]=dp[lc[u]][1]+dp[rc[u]][1]+s1;
}
int main()
{int Test,x,y,k;read(Test);while(Test--){read(n),read(m),tp=tot=0;for(int i=1;i<2*n;i++) G[i].clear(),lc[i]=rc[i]=0;for(int i=1;i<n;i++){read(h[i]);while(tp&&h[i]>=h[S[tp]]) lc[i]=S[tp--];if(tp) rc[S[tp]]=i; S[++tp]=i;}dfs0(S[1],0);while(m--){read(x),read(y),read(k),x=pos[x];for(int i=Log;i>=0;i--) if(f[x][i]&&h[f[x][i]]<=y) x=f[x][i];G[x].push_back(make_pair(y,k));}dfs(S[1]);printf("%d\n",dp[S[1]][0]);}
}