电磁波专题
电磁波、无线电、射频
电磁波 电磁波是由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动，其传播方向垂直于电场与磁场构成的平面，有效的传递能量和动量。电磁辐射可以按照频率分类，从低频率到高频率，包括有无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线等等。人眼可接收到的电磁辐射，波长大约在380至780纳米之间，称为可见光。只要是本身温度大于绝对零度的物体，都可以发射电磁辐射，而世界上并不存在温
![[机缘参悟-160] ：人的感知系统是及其有限的，从电磁波的频谱、声波的声谱，看人类只看感知到物质世界的一小部分，无法感知到全部真相](https://img-blog.csdnimg.cn/direct/50b8438105a24bb19f0bcd0621c03947.png)
[机缘参悟-160] ：人的感知系统是及其有限的，从电磁波的频谱、声波的声谱，看人类只看感知到物质世界的一小部分，无法感知到全部真相
目录 一、人自身是如何感知物质世界的？ 1.1 五官 1.2 关于视觉、光、电磁波 1.2.1 视觉系统 1.2.2 感光细胞 编辑 1.2.3 光波与人眼的光波范围 1.2.4 电磁波 1.2.5 通过科学仪器和技术可以拓展人对电磁波的感知 1.2.6 太阳光的光谱 1.2.6 光不仅仅用于传输视觉，还用来传输能量 1.3 关于听觉、声音、声波 1.3.1 人的听觉系
电磁波的波长与频率是什么关系？
摘要: 电磁波的波长（λ）与频率（f）之间的关系可以通过以下公式来表示： f = c/λ c=λ×f 其中： c 是光速，即电磁波在真空中的传播速度，约为 3 x 10⁸ 米/秒（m/s）λ 是波长，单位通常是米（m）f 是频率，单位是赫 ... 电磁波的波长（λ）与频率（f）之间的关系可以通过以下公式来表示： f = c/λ c=λ×f 其中： c 是光速，即电磁波在真空中的传播速度，
电磁波看不见摸不着，这个年轻人的奇思妙想改变了世界
转载： https://baijiahao.baidu.com/s?id=1608783152107830498&wfr=spider&for=pc 01 电磁波的发现 “成功了，这就是电磁波！” 滋......滋......滋.....，一束微弱而美丽的蓝色电火花在两个铜球间之间穿梭跃动，伴随着一个年轻人兴奋地喊声。 这个年轻人就是赫兹，彼时的他正在为发现了电磁波而兴奋不已
导行电磁波从纵向场分量求其他方向分量的矩阵表示
导行电磁波从纵向场分量求解其他方向分量的矩阵表示 导行电磁波传播的特点 电磁波在均匀、线性、各向同性的空间中沿着 z z z轴传播，可用分离变量法将时间轴、 z z z轴与 x , y x,y x,y轴分离，电磁波的形式可表示为： E ⃗ = E ⃗ ( x , y ) e − γ z e j ω t H ⃗ = H ⃗ ( x , y ) e − γ z e j ω t \begin{al
导行电磁波从纵向场分量求其他方向分量的矩阵表示
导行电磁波从纵向场分量求解其他方向分量的矩阵表示 导行电磁波传播的特点 电磁波在均匀、线性、各向同性的空间中沿着 z z z轴传播，可用分离变量法将时间轴、 z z z轴与 x , y x,y x,y轴分离，电磁波的形式可表示为： E ⃗ = E ⃗ ( x , y ) e − γ z e j ω t H ⃗ = H ⃗ ( x , y ) e − γ z e j ω t \begin{al
【你也能看得懂的电磁场与电磁波系列连载 20】
在上一篇连载里面，我们证明了为什么： 同时也得到了 M a x w e l l Maxwell Maxwell 方程中描述电场和磁场公式的微分形式： 那么在今天的连载里面，我们重点想看看闭合曲线的线积分应该如何变成微分形式。 我们回顾一下我们对闭合曲面的面积分的微分处理——我们让闭合曲面 S 不断缩小，那么意味着闭合曲面 S 所包围的体积也是不断趋于0. 然后我们再同时除以闭合曲面
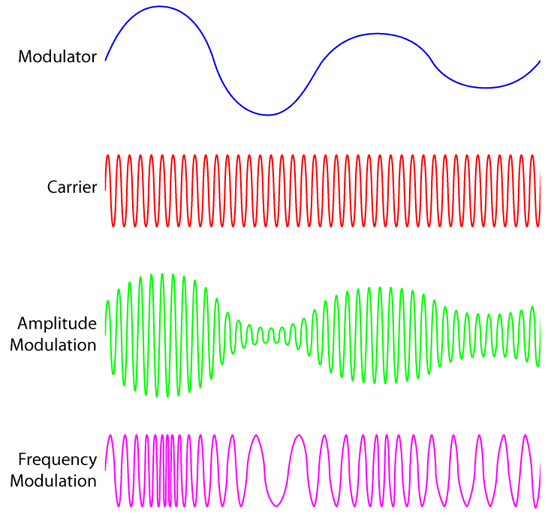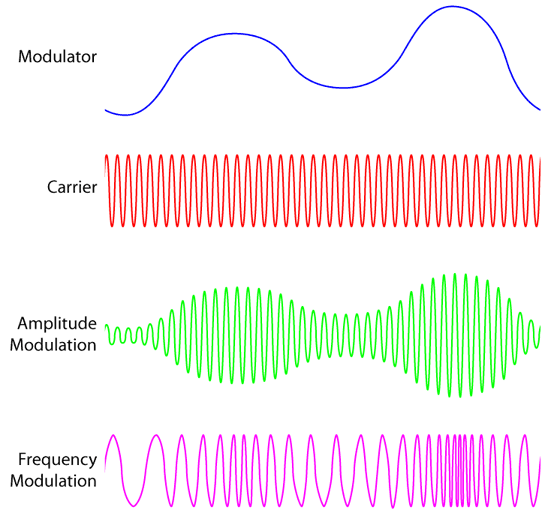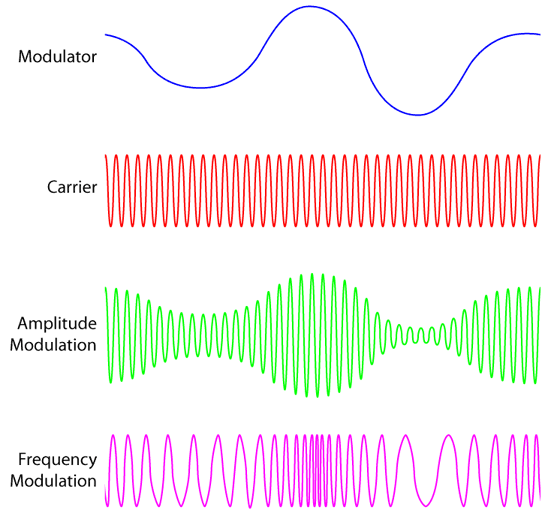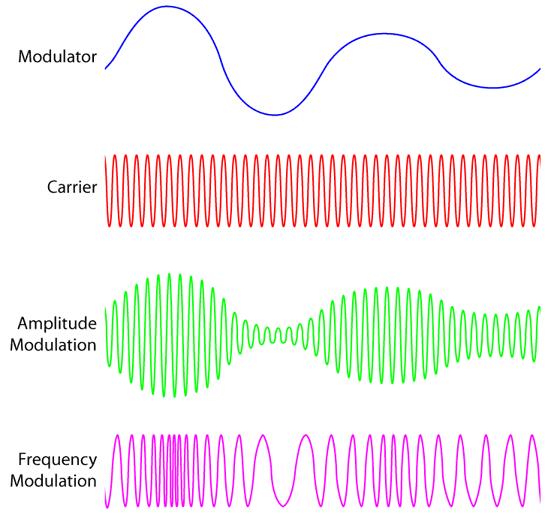
信号是怎么搞到电磁波上面去的呢？
在之前的文章中，我们曾多次讲到电磁波的美妙，但是有了电磁波就可以通信了吗？ No，我们要把信息加载到电磁波上，这个电磁波就可以作为信息的载体来工作了。可是信号是怎么加载到电磁波上的呢？ 今天我们一起来介绍几种最基本的信号调试方式。虽然在现在的通信制式中，这些调制方式有很多的不足，但是作为信号入门的基础，我们不妨再花点时间复习一下呗。 AM：Amplitude Modulation, 幅度调制
《电磁场与电磁波》（谢处方第5版）anki卡片学习笔记txt文件输出
#separator:tab #html:true #tags column:9 矢量叉乘A×B= （用 A、 B的模表示具体的值） e nABsinθ 其中 e n为右手四个手指从矢量A到B旋转θ时大拇指的方向 矢量的叉积是否符合交换律和分配律 不符合交换律， A× B=- B× A 但符合分配律 A(a,b,c)和B(d,e,f)的叉积如何计算 “[\math
《电磁场与电磁波》（谢处方第5版）anki卡片学习笔记txt文件输出
#separator:tab #html:true #tags column:9 矢量叉乘A×B= （用 A、 B的模表示具体的值） e nABsinθ 其中 e n为右手四个手指从矢量A到B旋转θ时大拇指的方向 矢量的叉积是否符合交换律和分配律 不符合交换律， A× B=- B× A 但符合分配律 A(a,b,c)和B(d,e,f)的叉积如何计算 “[\math
电磁场与电磁波part6、7--均匀平面波的反射与透射、导行电磁波
1、分界面上的反射系数 反射波电场振幅 与入射波电场振幅 的比值，即： 2、驻波系数（驻波比） 合成波的电场强度的最大值与最小值之比，即： 3、导波系统中电磁波的传输问题属于电磁场边值问题，即在给定边界条件下解电磁波动方程。 4、空心导体波导中不能传播TEM波，金属空心波导内可以存在TM波和TE波。 5、模式判断 当工作频率 （工作波长
2021,2022考研电磁场电磁波考研核心题库免费分享
2021,2022考研电磁场电磁波考研核心题库免费分享 具体链接如下： csdn：链接：https://pan.baidu.com/s/1ZePJe2HMjFsYH0QCBPvOxQ 提取码：hfnw 复制这段内容后打开百度网盘手机App，操作更方便哦
基于定向发射的高能电磁波的物质创造机
基于定向发射的高能电磁波的物质创造机 (2016-12-01 13:32:46) [编辑] [url][删除]😐|-:😐|-:[/url] [url]转载▼:-||-:😐|-:[/url] 一、 研发背景 随着我国国民经济的不断发展，综合国力的显著增强，人民群众对人造合成物质的需求越来越大，国家急需一种人工合成物质的方法。 目前，常规合成物质是通过在高温高压的环境下使物质的原子结构
电磁波时域有限差分方法（FDTD）-C语言-FDTD和激励源和MUR边界
参考： 葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 西安电子科技大学出版社, 2011. Schneider J B. Understanding the Finite-Difference Time-Domain Method[J]. 2013. 最近要用FDTD做仿真，所以找了以上两本书，FDTD确实是有点难的。 想了想流程： 1：FDTD 2：激励源 3：吸收边界
无线传输技术 基础 电磁波 信息编码技术
电磁波 电磁波是电磁场的一种运动形态。电与磁可说是一体两面，变动的电会产生磁，变动的磁则会产生电。 引导性媒体(线缆媒体) 电磁波沿着一个固态媒体传播。例如：金属导体、玻璃或plastic 。光纤（单模 直线 多模 反射） 非引导性媒体(无线媒体) 提供了传输电磁信号的手段，但不加以引导。例如：大气层、外层空间。 波长和频率的关系 波长(λ) ：两个相邻的波峰之间
TI-CCxx系列电磁波唤醒学习笔记
最近用到TI的射频的片子，CCxx系列的价格还算便宜，用作低功耗还是不错的。当然最令人期望的还是无线唤醒（WOR），以前做过比较多的是利用深度睡眠与RTC唤醒。但是TI已经把这个功能做到了片子里面，在我看来，至少可以通过片子来唤醒MCU。功耗应该会有所下降的。 原创帖子，转摘注明出处：http://blog.csdn.net/libin55/article/details/51837903
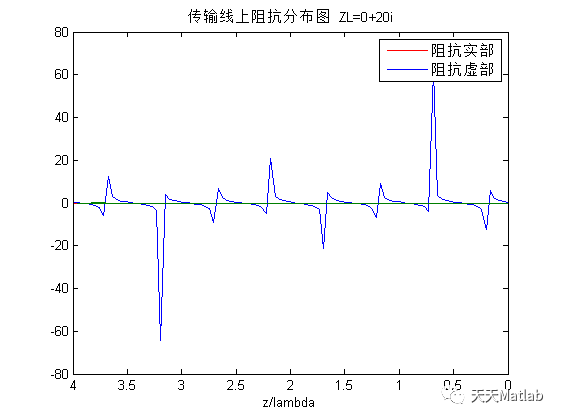
基于Matlab模拟传输线上电磁波仿真
✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。 🍎个人主页：Matlab科研工作室 🍊个人信条：格物致知。 更多Matlab仿真内容点击👇 智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统 信号处理 图像处理 路径规划
【你也能看得懂的电磁场与电磁波系列连载 14】
在上一个连载里面，我们通过静磁场的两个基本方程推导出了静磁场的边界条件。 那么今天的连载，我们将给大家看看这种形式的安培环路定理所带来的矛盾。 首先，我们看安培环路定理的左边部分：是磁场的曲线积分，那么讲道理它就应该只跟你这个曲面边界的形状有关。 在安培环路定理里，我们可以随意选一个曲面，然后所有穿过这个曲面的电流会在这个曲面的边界上形成一个环绕磁场。那么这个曲面如何选取就很有意思了。我们
【你也能看得懂的电磁场与电磁波系列连载 13】
在上一个连载里面，我们引入了真空和介质中的安培环路定理。那么这样，我们就可以非常方便地求解某些对称的磁场了。那么很电场类似，在学习磁场时，我们也需要讨论一下磁场的边界条件。 说实话，磁场边界方程的推导和静电场里面的思路几乎一模一样。所以我们这里简单看一看： 我们首先根据静磁场的第一个方程： 那么我们有： n ˉ ⋅ B 1 ˉ − n ˉ ⋅ B 2 ˉ = 0 \bar{n}\sdot
【转】电磁波传播的回路是怎样的，或者电磁波传播过程中有“地”吗？
作者：培根 霍格 链接：https://www.zhihu.com/question/296493596/answer/500378560 来源：知乎 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 以电流为例，由麦克斯韦方程组中的磁场旋度方程： 上式中右边第一项代表电流密度矢量（可以理解为导线上传播的电磁波），第二项代表位移电流（变化的电场，可以理解为空间辐射的