目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么？ 四、总结五、升华 一、背景介绍 人眼看到的美的东西，都可以从数学这个抽象的学科中得到明确的逻辑论证；这就是数学学科神奇的地方之一 二、思路&方案 1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇

题目链接： http://acm.fzu.edu.cn/problem.php?pid=1669 题目大意： 求满足以a、b为直角边，c为斜边，并且满足a + b + c <= L的直角三角形的个数。 思路： 勾股定理，a、b、c也就是本原毕达哥拉斯三元组，则满足： x = m^2 - n^2 y = 2*m*n z = m^2 + n^2 其中m > n，且若m为

题目链接： http://poj.org/problem?id=1305 题目大意： 给一个整数N，求N范围内的本原的毕达哥拉斯三元组的个数，以及N以内毕达哥拉斯三元组不涉及 数的个数。 思路： 本原毕达哥拉斯三元组x^2 + y^2 = z^2 满足 x = m^2 - n^2，y = 2*m*n，z = m^2 + n^2，其 中m > n，且若m为奇数，则n为偶数

随便找个学生，让他举出一位著名的数学家——如果他能想到的话，他往往会选择毕达哥拉斯。如果不是，也许他想到的是阿基米德。哪怕是杰出的艾萨克·牛顿，在两位古代世界的巨星面前也只能叨陪末座了。阿基米德是一位思想巨人，毕达哥拉斯或许算不上，但人们往往低估了他的贡献，他值得更多赞誉——不在于他做出了什么，而在于他推动了什么。         在公元前570年左右，毕达哥拉斯出生在爱琴海东部

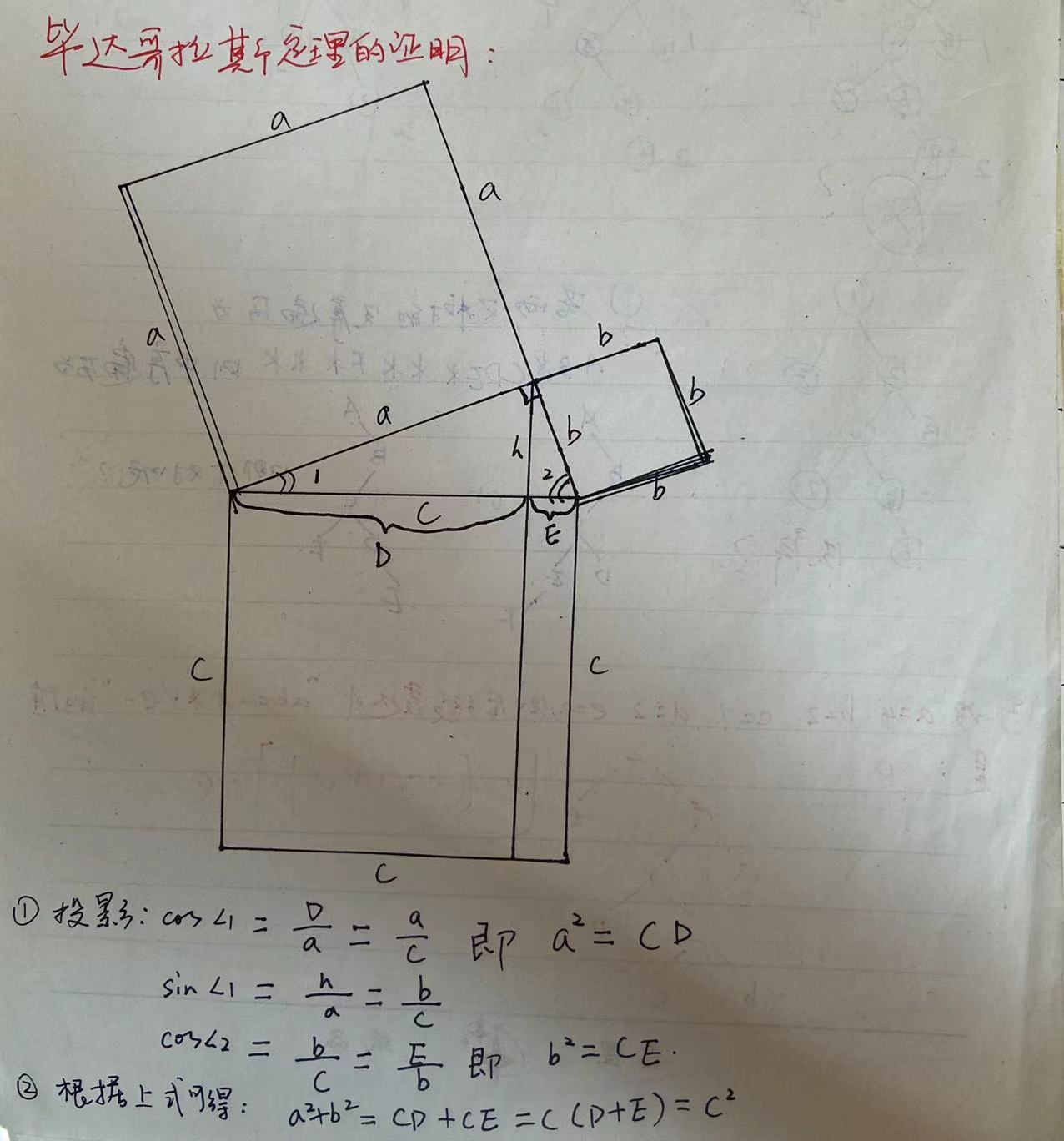
它告诉我们什么？ 直角三角形的三个边之间有什么关系。 为什么重要？ 它提供了几何和代数之间的重要联系，使我们能够根据坐标计算距离。它也催生出了三角学。 它带来了什么？ 测绘、导航，以及较近代出现的狭义和广义相对论——现有最好的关于空间、时间和重力的理论。 毕达哥拉斯定理的证明 古希腊人并没有将毕达哥拉斯定理表达为现代符号意义上的等式。那是随着代数的发展才出现的。在古代，该定理以

2000多年前毕达哥拉斯定理的证明方法，如下图：

【 毕达哥拉斯三元组】                                   X^2 + Y^2 = Z^2     满足这个方程的的正整数三元组被称为毕达哥拉斯三元组。     本原的毕达哥拉斯三元组，指如果一个毕达哥拉斯三元组x,y,z满足(x,y,z)=1,那么这个毕达哥拉斯三元组称为本原的。     [定理]:正整数x,y,z构成一个本原毕达哥拉斯三元组且y为偶数，当且仅

点击打开链接 Right-angled Triangle Accept: 52    Submit: 109 Time Limit: 1000 mSec    Memory Limit : 32768 KB  Problem Description A triangle is one of the basic shapes of geometry: a po