本文主要是介绍有趣的数学 毕达哥拉斯定理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
随便找个学生,让他举出一位著名的数学家——如果他能想到的话,他往往会选择毕达哥拉斯。如果不是,也许他想到的是阿基米德。哪怕是杰出的艾萨克·牛顿,在两位古代世界的巨星面前也只能叨陪末座了。阿基米德是一位思想巨人,毕达哥拉斯或许算不上,但人们往往低估了他的贡献,他值得更多赞誉——不在于他做出了什么,而在于他推动了什么。
在公元前570年左右,毕达哥拉斯出生在爱琴海东部的希腊萨摩斯岛。他是一位哲学家和几何学家。我们对他的生活所知甚少,而且信息都来自很久之后的记述,其历史准确性存疑,但关键事件很可能是对的。公元前530年左右,他搬到古希腊殖民地克罗顿(今意大利)。他在那里创立了一个哲学宗教团体——“毕达哥拉斯学派”,他们相信宇宙是基于数字的。时至今日,其创始人的名声就来自以他的名字命名的定理。这个定理已被教授了两千多年,还进入了流行文化。

由于历史的不可考,现代人并不知道毕达哥拉斯是否真的证明了他的定理。事实上,根本不知道这是否是他的定理。它完全有可能是毕达哥拉斯的一个仆从,或某个古巴比伦或苏美尔的抄写员发现的。但人们把它归功于毕达哥拉斯,他的名字就流传下来了。无论其起源如何,这个定理和它的结果对人类历史产生了巨大的影响。它们的的确确拓展了我们的世界。
古希腊人并没有将毕达哥拉斯定理表达为现代符号意义上的等式。那是随着代数的发展才出现的。在古代,该定理以口头和几何的方式表达。亚历山大里亚的欧几里得的著作记载了它最优雅的形式,这也是它的第一个文献证据。公元前250年左右,欧几里得写下了著名的《几何原本》——有史以来最具影响力的数学教科书,成为第一位现代数学家。
欧几里得把几何学变成了逻辑:他明确地列出了自己的基本假设,并援引这些假设,为他的所有定理提供系统的证明。他建造了一座概念之塔,其基础是点、线和圆,而塔尖则恰好存在五种正多面体。
欧几里得几何“王冠上的明珠”就是我们现在所说的毕达哥拉斯定理:《几何原本》第一卷中的命题47。在托马斯·希思爵士的著名译本中,这个命题是这样写的:“在直角三角形中,直角所对的边上的正方形等于夹直角的边上的两个正方形。”
就高等数学而言,古希腊人使用的是直线和面积,而不是数字。所以毕达哥拉斯和他的古希腊后人将这个定理解释为面积相等:“用直角三角形中最长边构造的正方形面积,是由另外两边构造的正方形面积的和。”最长的一条边就是著名的“斜边”(hypotenuse),意思是“在下面拉伸”。如果你以恰当的方向画图,确实如此,如下图(左)所示。
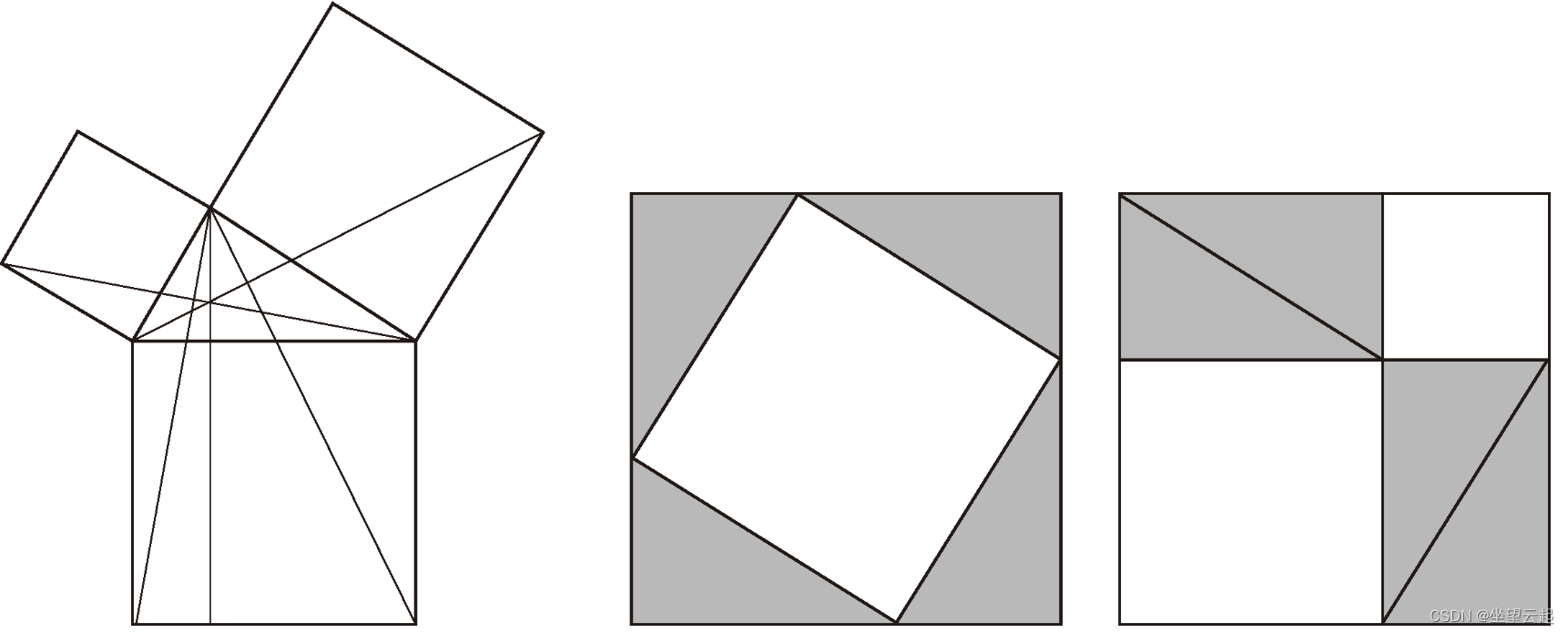
左:欧几里得证明毕达哥拉斯定理的构造线。中和右:定理的另一证明。外部正方形的面积相等,阴影三角形的面积也相等。因此,倾斜的白色正方形面积等于其他两个白色正方形面积之和。
2000年后,毕达哥拉斯定理就被重写为代数方程,毕达哥拉斯方程有许多用途和意义。最直接的是,给定另外两边,它可以让你计算斜边的长度。
我们在现实生活中遇到的许多三角形都不是直角三角形,因此方程的直接应用似乎有限。但是,任何三角形都可以分割成两个直角三角形,而任何多边形都可以分割成若干三角形。因此,直角三角形是关键:它们证明了三角形的形状与其边的长度之间存在有用的关系。从这一见解中发展出来的学科是三角学——“三角形的测量”。
直角三角形是三角学的基础,特别是它决定了基本的三角函数:正弦、余弦和正切。这些名称源于阿拉伯语,而这些函数及其许多前辈的发展史,展示了今天这个版本经历了什么样的复杂路径。
欧几里得《几何原本》中的毕达哥拉斯定理的证明,把这个定理牢牢地限定在欧氏几何的范围内。“欧氏几何”这个词一度可以直接换成“几何”,因为我们通常认为欧氏几何就是物理空间的真实几何。
但事实并非如此,后面若干年又发展出来椭圆几何(黎曼几何)、罗氏几何(双曲几何)等,都是非欧几里得几何,并且这些新的几何与欧氏几何一样逻辑自洽,遵循了除了平行公理之外的所有公理。
这篇关于有趣的数学 毕达哥拉斯定理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







