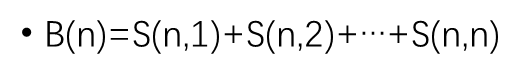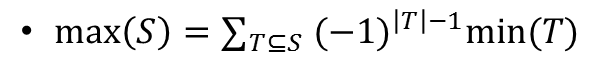8.14 快不行了。 DP 经典背包问题 • n个物品，每个物品有重量 w[i]，求选出重量量和不超过 S 物品集合的方案数 • 01背包：每个物品最多选⼀次 • ⽆限背包（完全背包）：每个物品可以选无数次 • 多重背包：每个物品最多选 k[i] 个 进阶背包问题1 • 考虑01背包问题，有 Q 种操作，每次加入一种物品或删除一种物品，每次操作完后输出不超过 S 的⽅方案数 •

8.12 “简单”DP 好的，那么在这里，我们又讲到了斯特林数以及贝尔数，这两个在上一篇博客上已经提到过了 抛下链接：Day15 欧拉数 这里是百度百科 • n个数的排列，其中有k个满足Pi<Pi+1的排列个数 • E(n,k)=(k+1) * E(n-1,k)+(n-k) * E(n-1,k-1) 斯特林数、欧拉数的求和技术及应用 从左到右填数，记录上一个填的在未填数中的排名

8.11 数学期望与组合计数 双射 “一一对应” 双射一定满足|A|=|B| 单射就是只能一对一，不能多对一 满射只要Y中的元素在X中都能找到原像就行了(一对一，多对一都行). 双射就是既是单射又是满射(一个对一个,每个都不漏掉). 单射 满射 双射 减法原理 · 有两个事件A,B，要么A发生要么B发生，现在知道了（A,B中某个发生）的方案数，以及A发生的方案数，求B发生

8.10 今天讲的例题部分Day1讲过，这里不重复了，见Day1博客 数学期望与组合计数 期望的定义 期望的线性性 E(x1 + x2) = E(x1) + E(x2) 期望的平方和平方的期望不同 E( (x1 + x2)2 ) = E( (x1)2) + E( (x2)2 ) + 2E(x1x2) 当x = 0或1 时， x2 = x 一个重要的等式 1 + x + x2

8.9 我睡过头了！！！！ 好饿~~~~噫 简单数论（！？!!!∑(ﾟДﾟノ)ノ） 是的，又是它 先讲了一些基本定义啊之类的 然后从欧几里得开始 提了下裴蜀定理， 即若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。 接着是扩展欧几里得 这个时候讲到了小凯的疑惑 小凯手中有两种面值的金

8.8 贪心 讲了一堆例题 从普及到语言入门的贪心应用实例（Excuse me？） 找零问题 你去商店买东西， 收银员要找给你 ? 元。 一共有面值为 500, 100, 50, 10, 5, 1 的六种硬币。(硬币？——来自博主的发问） 你希望拿到的硬币数量尽可能地少。 贪心，尽可能多的拿面额大的硬币 区间覆盖问题 在一条数轴上有 ? 个互不相交的区间，现在你需要画不超过 ?

8.13 模拟赛 A - SR无敌 发现了一点规律，同时注意一些小细节就可以做出来了 code（这是比较精简的程序，自己的又臭又长） #include <bits/stdc++.h>#define ll long long#define lowbit(x) x & (-x)#define memset(x) memset(x, 0, sizeof(x))#define N 100

8.7 在这个欢乐的七夕佳节，我们迎来了欢乐的ACM 于是，在和yjz大佬和yy大佬严肃（？）讨论后，我们的队名就叫七夕“快乐”（为什么加引号就不说了，qq情头是和小号的某） 在前一天，去商场的时候看到几个小朋友手上粉色爱心型的气球，某和yjz大佬拉着yy大佬绕着商场走了一圈找到了发气球的那家店，愣是没好意思进去要，结果回来的路上，十分幸运的看到地上有个，刚想去捡，只见一个老爷爷捉住气球，五

注 本文中max[l, r]表示区间[l, r]中最大值 min[l, r]同理 Part 1 分治 经典例题 • 求所有区间的最⼤值之和 一个最大值，对L在它左边R在它右边的所有区间都有贡献 O(n) • 求所有区间的最⼤值*最⼩值之和 对于一个区间|L --- mid --- R| 处理出[mid, R]中\(min,max,min*max\)的前缀和 然后对于\(L \leq i \leq