想要求pytorch tensor中某个2048维度的向量的模长，可以先相乘，然后再用sum求和。 假设 v是一个2048维的向量，则可以利用一下两个语句求出模长的平方。 sq = v * vsum_sq = sq.sum()

为什么两个向量的内积等于模长乘夹角？   已知两个向量 a = [ a 1 , a 2 ] a=[a_1,a_2] a=[a1​,a2​]和 b = [ b 1 , b 2 ] b=[b_1,b_2] b=[b1​,b2​]，他们的内积为 a b = a 1 b 1 + a 2 b 2 ab=a_1b_1+a_2b_2 ab=a1​b1​+a2​b2​，看书上的定义该内积的值是一个

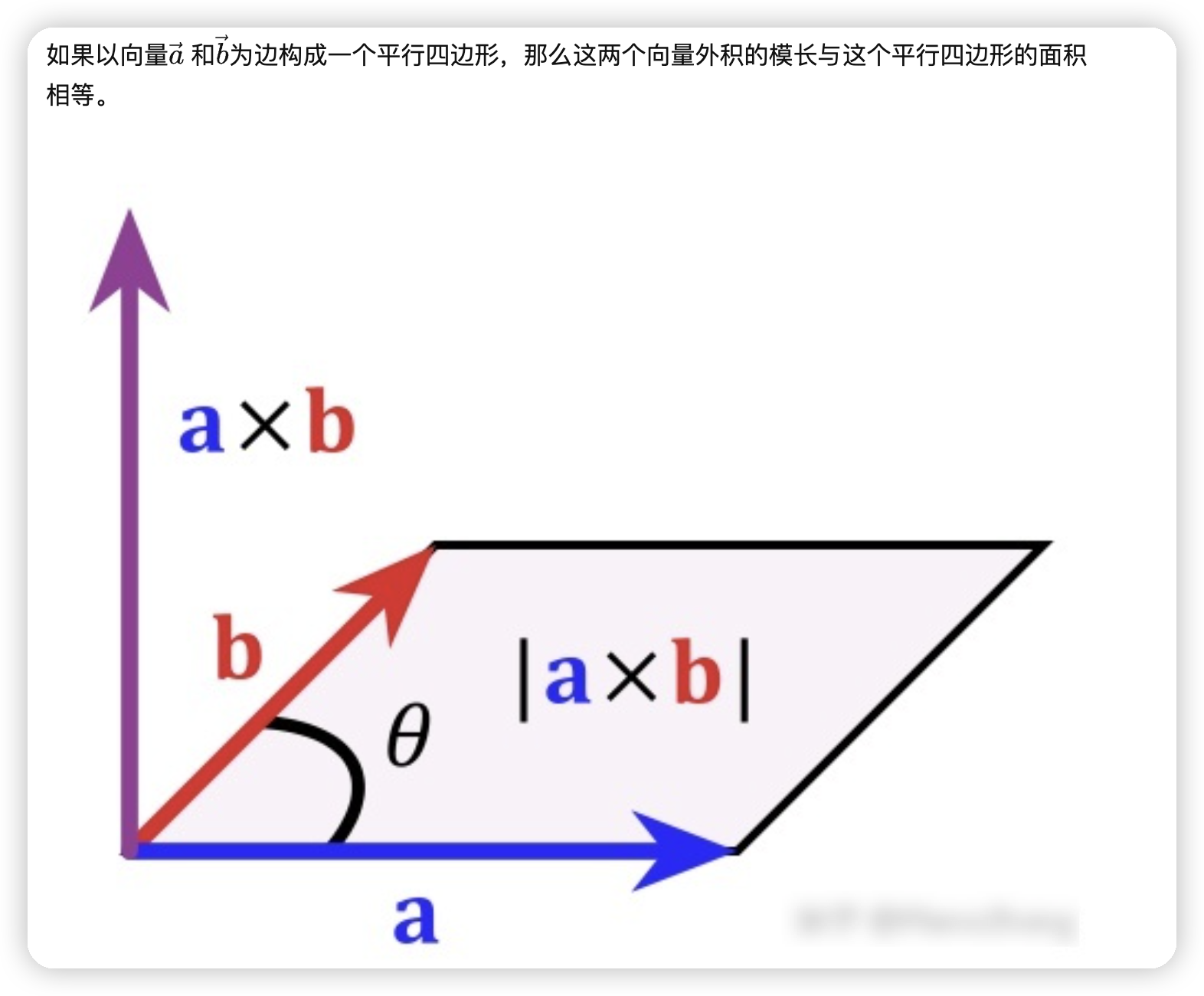
文章目录 一、向量点乘（内积）1.1 几何意义1.2 点乘的代数定义，推导几何定义（用于求向量夹角）1.2.1 余弦定理 1.3 程序计算 二、向量叉乘（外积）2.1 几何意义 三、通俗理解内积和外积四、向量的模长 向量点乘、叉乘的概念和意义 一、向量点乘（内积） 点乘（Dot Product）的结果是点积，又称数量积或标量积（Scalar Product）。 1.1

题目描述： 题目分析： 略微转化后，即给出一些向量 ( a i x i , b i x i , c i x i ) (a_ix_i,b_ix_i,c_ix_i) (ai​xi​,bi​xi​,ci​xi​)，其中 x i x_i xi​是随机分布在 [ 0 , 1 ] [0,1] [0,1]的实数，设 R R R为向量全部相加后的模长，求 E ( R 4 ) E(R^4) E(R4) 思