关于暇点型反常积分的收敛性判别 @(微积分) 积分上下限确定的积分，在上下限范围内存在着暇点，此时应该怎么做比较容易分析出积分是否收敛是个很有意思的问题。 不加证明的总结一个有效的解决思路：假设在(a,b)上，f(a)趋向于无穷大。则积分 ∫baf(x)dx \int_a^bf(x)dx是否收敛。 方法是： 判定limx→a+f(x)(x−a)δ是否存在，其中δ∈(0,1)

一、背景知识 DMP作为轨迹生成方法的一种，具有诸多优势，如弹簧阻尼二阶系统保证了他可以收敛到目标点，且具有良好的时间和空间上的泛化能力。我最近一直在想为什么该系统可以保证运动轨迹收敛到目标点 g g g，后来看了码农家园的博客以及对照论文中的内容有了一定的理解，下面给出DMP算法详细的收敛性证明。 二、从微分方程的角度出发 利用本科阶段学到的高等数学知识，我们先求解一个微分方程： f ˙

完美的学习算法 昨天和同学在群里讨论DRL里bad case的问题。突然有同学提出观点：“bad case其实并不存在，因为一些算法已经理论证明了具有唯一极值点，再加上一些平滑技巧指导优化器，就必然可以收敛。” 当听到这个观点时，我是一时语塞。因为当前深度学习研究的最大问题就是，花了很大资源训练的千万参数神经网络根本不work，一切都白白浪费。因此才有NAS之类方法尝试根据一些训练初期的动力学

完美的学习算法 昨天和同学在群里讨论DRL里bad case的问题。突然有同学提出观点：“bad case其实并不存在，因为一些算法已经理论证明了具有唯一极值点，再加上一些平滑技巧指导优化器，就必然可以收敛。” 当听到这个观点时，我是一时语塞。因为当前深度学习研究的最大问题就是，花了很大资源训练的千万参数神经网络根本不work，一切都白白浪费。因此才有NAS之类方法尝试根据一些训练初期的动力学

第 3 章  Fourier级数的收敛性(Convergence of Fourier Series) The sine and cosine series, by which one can represent an arbitrary function in a given interval, enjoy among other remarkable properties that of

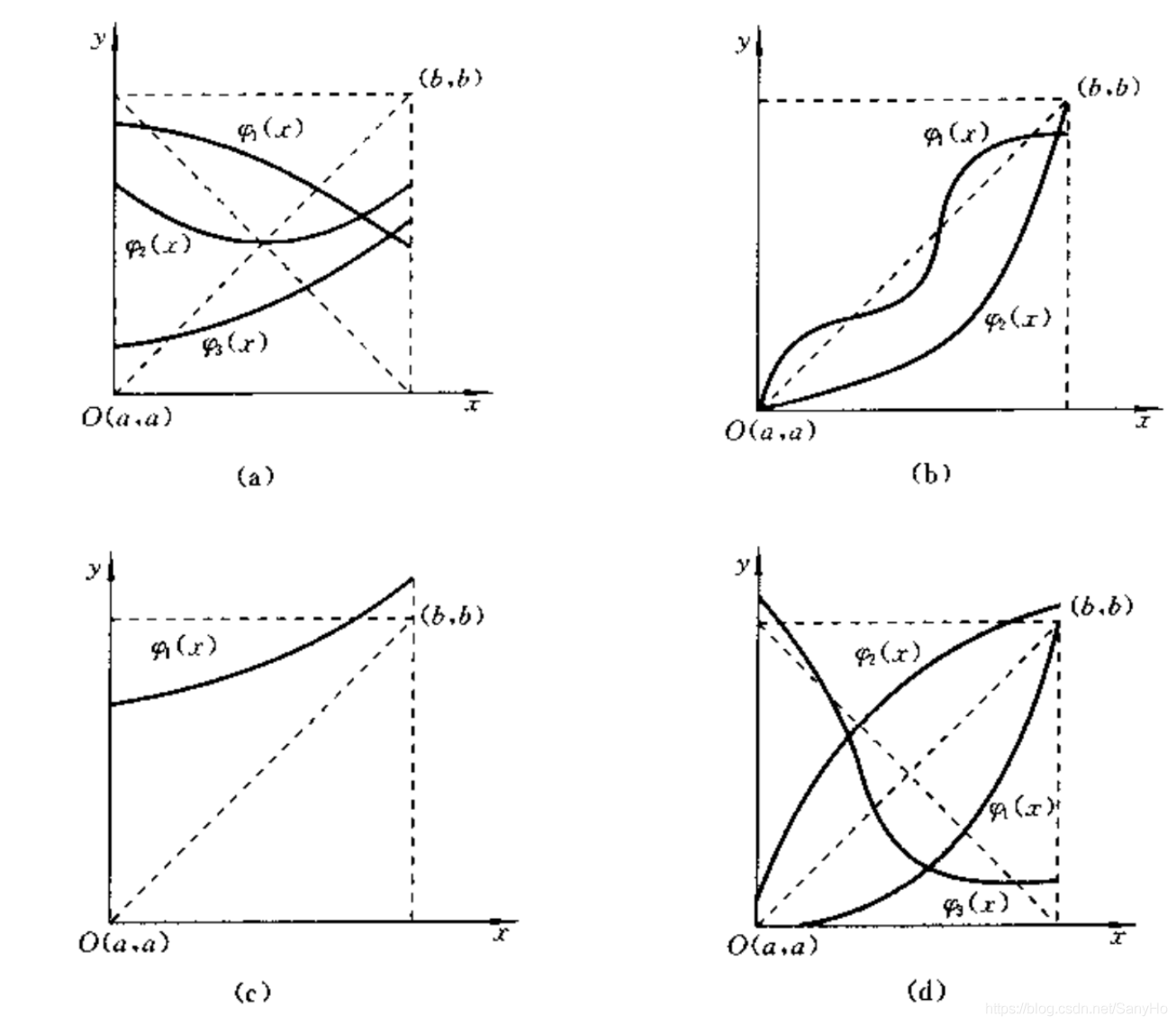
一般迭代法 1. 基本原理和迭代公式 先看一个例子。设有两个函数 y = φ ( x ) y=\varphi(x) y=φ(x)和 y = x y=x y=x，欲求其交点 x ∗ x^* x∗。为此，可将函数 y = x y=x y=x改写成 x = y x=y x=y的形式，并给定一个初始值 x 0 x_0 x0​，并进行如下计算： （1）先计算函数 y = φ ( x ) y=\varp

1.TCP拥塞的本质 注意，我并没有把题目定义成网络拥塞的本质，不然又要扯泊松到达和排队论了。事实上，TCP拥塞的本质要好理解的多！TCP拥塞绝大部分是由于其”加性增，乘性减“的特性造成的！         也就是说，是TCP自己造成了拥塞！TCP加性增乘性减的特性引发了丢包，而丢包的拥塞误判带来了巨大的代价，这在深队列+AQM情形下尤其明显。         我尽可能快的解释。争