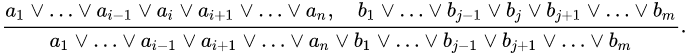归结专题
人工智能——基于谓词逻辑的归结原理
实验二 归结原理实验 一、实验目的 加深学生对归结原理进行定理证明过程的理解,掌握基于谓词逻辑的归结过程中子句变换过程、替换与合一算法和归结策略等重要环节,进一步了解实现机器自动定理证明的步骤。 二、实验内容 对于任意一阶谓词逻辑描述的定理,给出基于归结原理的证明过程。如输入: A1 : ("x)(P(x)®(Q(x) ÙR(x))) A2 : ("x)(P(x) Ù S(x))
归结原理、归结演绎推理
主要内容 归结演绎推理范式子句与子句集将谓词公式转化为子句集命题逻辑鲁宾逊归结原理 归结演绎推理 定理证明的实质是对前提P和结论Q证明P →Q的永真性应用反证法,欲证明P →Q,只要证明 P∧~Q 等价于 F鲁宾逊归结原理对机械化推理有重大突破鲁宾逊归结原理是以子句为背景开展研究的 范式 什么是范式:“范式” 是一个用于表示、简化或标准化特定类型数据或表达式的术语。它通常用于不同领域,如
(《机器学习》完整版系列)第15章 规则学习——15.3 归结与逆归结(你可知“反证法”原理?)
归结原理(即消解):可以“消除”该互补项 归结与逆归结 上篇我们用“十一条规则”形成一套命题逻辑的形式推理体系,归结原理强大到只需一个规则就可形成一套命题逻辑的形式推理体系。 若互补项(即正文字 L L L与负文字 ¬ L \lnot L ¬L)分别在两子句 C 1 C_1 C1与 C 2 C_2 C2中,则可以“消除”该互补项,称为归结原理(即消解),如图15.1 所示。 C = C
用python解决归结反演的问题
用python解决归结反演的问题 一、实验目的二、实验思路三、代码及注解 一、实验目的 二、实验思路 第一步:先将子句集转换为数字表示,这样利于判断归并,相加为0即可 第二步:从子句集中取出2个进行归并判断 第三步:完成判断后进行移除数据和查重处理,然后将新子句集加入总子句集中 第四步:判断总子句集中的最后一个元素是否为空,为空的话证明归结成功 三、代码及注解 # 非
人工智能推理——归结反演,学习记录
自己也是一个在为期末考试加班赶点的大学牲,考试前对归结反演这一部分进行了“复习”(平时学校课程安排的不太好,所以和预习差不多),下面是我在学完以后的个人理解,通过博客的形式让自己巩固加深一下,顺便给更多对归结反演有困难的人一些帮助。如果大佬们觉得有哪些地方不对的希望能在评论区里批评一下。下面是正文: 1.归结反演的原理: 如果通过多个条件可以推出一个结论是恒对的,那么通过一样的
代码逻辑归结起来分为几个部分
网络结构前向数据流(forward) 有了网络结构,我们还需要将网络数据流串联起来,这个过程普遍成为forward, LOSS优化 optim训练和梯度下降
Python小实验——归结反演
实验目的 打印所有互补文字; 头现命题逻辑简单归结; 实验内容及结果 # 归结反演过程,传入外面最大的数组里面的两个小数组,也就是两个子句,消掉对应的谓词公式def result(m=[],n=[]):after=0while len(m)!=after:after=len(m)for i in m:for j in n:if (int(i) + int(j) ==0):m.remove
人工智能基础——鲁宾孙归结原理
鲁宾孙归结原理: 命题逻辑中的归结原理: 若r1,r2是一个子句集中的两个子句,r1,r2中含有互补文字,那么把r1,r2拿出来,去掉互补文字,再把剩下的部分析取,得到的子句r12为r1,r2的归结式,r1,r2为r12的亲本子句。 r12与,r1∧r2是等价的,假设正文字在r1中,负文字在r2中,在r1中我们可以把该正文字换到析取符号的后面,然后用蕴含等价变换,r2中的负文字在析取符号前面,然后
高级人工智能.归结原理完备性证明(详细)
写在最前 本文为博主复习高级人工智能这门课程时,针对于归结原理完备性证明这一问题,所做的笔记。这是国科大本门课程的必考题,步骤较为详细,建议理解后记忆。 回顾:归结原理 在命题逻辑中的归结规则是一个单一的有效的推理规则,从两个子句生成它们所蕴含的一个新的子句。归结规则接受包含互补的文字的两个子句 - 子句是文字的析取式,并生成带有除了互补的文字的所有文字的一个新子句。形式上,这里的ai和bj