人工智能——基于谓词逻辑的归结原理

2024-02-05 11:20
文章标签 逻辑 原理 谓词 人工智能 归结

本文主要是介绍人工智能——基于谓词逻辑的归结原理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

实验二 归结原理实验

一、实验目的

加深学生对归结原理进行定理证明过程的理解，掌握基于谓词逻辑的归结过程中子句变换过程、替换与合一算法和归结策略等重要环节，进一步了解实现机器自动定理证明的步骤。

二、实验内容

对于任意一阶谓词逻辑描述的定理，给出基于归结原理的证明过程。如输入：

A1 ： ("x)(P(x)®(Q(x) ÙR(x)))

 A2 ： ("x)(P(x) Ù S(x))

        G ：  ($x)(S(x)ÙR(x))

要证明：G是A1和A2的逻辑结果。

三、实验环境

推荐使用C++语言，编译器推荐使用Microsoft Visual Studio Professional 2019(version=16.3.8)。

四、实验原理

归结原理是一种推理规则。从谓词公式转化为子句集的过程中看出，在子句集中子句之间是合取关系，其中只要有一个子句不可满足，则子句集就不可满足。若一个子句集中包含空子句，则这个子句集一定是不可满足的。归结原理就是基于这一认识提出来的。

应用归结原理进行定理证明的过程：

设要被证明的定义表示为：

A1∧A2∧…∧An→B

(1)首先否定结论B，并将否定后的公式¬B与前提公式集组成如下形式的谓词公式：G= A1∧A2∧…∧An∧¬B。

(2)求谓词公式G的子句集S。

(3)应用归结原理，证明子句集S的不可满足性。

五、实验步骤

步骤一 设计谓词公式的存储结构，即内部表示，注意对全称量词"x和存在量词$x可采用其他符号代替。

原符号

替换符号

全称量词∀

@

存在量词∃

#

析取符号∨

|

合取符号∧

&

取反符号¬

~

蕴含符号→

>

例如A1 ： ("x)(P(x)®(Q(x) ÙR(x)))，输入的时候要替换为A1：(@x)(P(x)>(Q(x)&R(x)))。

核心代码如下所示：

typedef string Formula; //谓词公式
typedef vector<string> SubsentenceSet;
typedef map<string,int> SubsentenceMap;
typedef string::iterator FormulaIter;  //迭代器
typedef string::reverse_iterator FormulaRevIter;  //反向迭代器
typedef vector<string>::iterator VectorIter;
typedef vector<string>::reverse_iterator VectorReIter;
map<string, string> m1;
int clause[20]; // 用这个来记录被删除的子句
/*("x)(P(x)®(Q(x) ÙR(x)))，输入的时候要替换为A1：(@x)(P(x)>(Q(x)&R(x)))。*/
// 公式符号定义
const char EQ = '#';          // 存在量词符号
const char UQ = '@';          // 全称量词符号
const char IMPLICATION = '>'; // 蕴含符号
const char NEGATION = '~';    // 否定符号
const char CONJUNCTION = '&'; // 合取符号
const char DISJUNCTION = '|'; // 析取符号
const char CONSTANT_ALPHA[] = {'a', 'b', 'c', 'd', 'e','i', 'j', 'k'};

步骤二 变换子句集，可按以下过程变换，变换过程的核心代码如下所示：

1、消去蕴含连接词。

FormulaRevIter GetBeginOfFormula(FormulaRevIter position,FormulaRevIter rend){//考虑用栈来找到蕴含前件int location;bool isFormula=true;//判断是不是蕴含前件是一个整体还是一个公式，公式是true，整体是falsestack<char> seek; //创建一个栈++position; //逆向回退1while(position!=rend){ //循环没有结束if(*position.base()==')') //如果是‘)’入栈seek.push(*position.base());if(seek.size()>1)isFormula=false;    //说明括号不止一个，是个整体if(*position.base()=='(') //如果是'('出栈seek.pop();if(seek.empty()==1){ //如果栈为空,说明已经找完了蕴含前件了if(isFormula)return position; //这里需要注意一下 正向迭代器与反向迭代器之间的关系elsereturn position-1;}position++;}return rend;//要么返回第一个字符的位置
}// 1、消去蕴含连接词。
Formula& RemoveImplication(Formula& f)
{FormulaIter iter;while((iter = find(f.begin(), f.end(), IMPLICATION))   //找蕴含符号!= f.end()) {*iter = DISJUNCTION; // 将蕴含符号替换为析取符号FormulaRevIter revIter(iter);revIter =GetBeginOfFormula(revIter, f.rend()); // 查找蕴含前件   //发f,rend()正数第一个字符iter = revIter.base()-1;// 反向迭代器到正向迭代器转换需要减1f.insert(iter, NEGATION);	// 在前件前面插入否定}return f;
}

2、将否定符号移到紧靠谓词的位置。

Formula& MoveNegation(Formula& f)
{FormulaIter iter = find(f.begin(), f.end(), NEGATION);while(iter != f.end()) {if(*(iter+1) == '(') {// 否定不是直接修饰谓词公式，需要内移// 否定符号修饰着带量词的谓词公式if(*(iter+2) == EQ || *(iter+2) == UQ) {// 量词取反*(iter+2) == EQ ? *(iter+2) = UQ : *(iter+2) = EQ;string leftDonePart(f.begin(), iter+5);// cout<<leftDonePart<<endl;// 移除否定符号leftDonePart.erase(find(leftDonePart.begin(),leftDonePart.end(), NEGATION));string rightPart(iter + 5, f.end());// 否定内移rightPart.insert(rightPart.begin(), NEGATION);// 递归处理右部分MoveNegation(rightPart);string(leftDonePart + rightPart).swap(f);return f;}else {	// 修饰着多个公式，形如~(P(x)|Q(x))iter = f.insert(iter+2, NEGATION);	// 内移否定符号while(1) {iter = FindFormula(iter, f.end());         //用来找是否有谓词公式？assert(iter != f.end() && "No Predicate Formula!");  //断言FormulaIter iter2 = FindPairChar(                   //找到整个谓词公式iter, f.end(), '(', ')');++iter2;if(IsConnector(*iter2)) {  //判断是不是合取符号和析取符号*iter2 == DISJUNCTION ? *iter2 = CONJUNCTION: *iter2 = DISJUNCTION;iter = f.insert(iter2+1, NEGATION);   //插上否定}elsebreak;}f.erase(find(f.begin(), f.end(),NEGATION));// 清除原否定符号return MoveNegation(f);}}else if(*(iter+1) == NEGATION) {// 两个否定，直接相消f.erase(iter, iter + 2);return MoveNegation(f);	// 重新处理}else {// iter = find(iter + 1, f.end(), NEGATION);   //这行代码是错误的//这里应该还要加上递归，不然就会消除掉第一个否定产生错误string leftDonePart(f.begin(), iter + 1);string rightPart(iter + 1, f.end());MoveNegation(rightPart);string(leftDonePart + rightPart).swap(f);return f;}}return f;
}

3、适当改名使量词间不含同名指导变元，对变元标准化。

Formula& StandardizeValues(Formula& f)
{set<char> checkedAlpha;FormulaIter iter = FindQuantifier(f.begin(), f.end());while(iter != f.end()) {char varName = *++iter;	// 获取变量名if(checkedAlpha.find(varName) == checkedAlpha.end()) {  //如果set里面没有该变量名字，就加入checkedAlpha.insert(varName);}else {	// 变量名冲突了，需要改名// 获取新名子char newName = FindNewLowerAlpha(checkedAlpha);checkedAlpha.insert(newName); //这里在源代码的基础上加入一个 要加入新生成的变量名字// 查找替换右边界FormulaIter rightBorder = FindPairChar(iter + 2, f.end(), '(', ')');// 将冲突变量名替换为新的名子*iter = newName;replace(iter, rightBorder, varName, newName);iter = rightBorder;	// 移动到新的开始}iter = FindQuantifier(iter, f.end());}// 调试// for (set<char>::iterator it = checkedAlpha.begin(); it != checkedAlpha.end(); it++)// 	cout << *it << " ";return f;
}

4、化为前束范式。

Formula& TransformToPNF(Formula& f){FormulaIter iter = FindQuantifier(f.begin(), f.end());if(iter == f.end())return f;else if(iter-1 == f.begin()) { // 量词已经在最前面iter += 3;string leftPart(f.begin(), iter);string rightPart(iter, f.end());TransformToPNF(rightPart);  // 递归处理右部分(leftPart + rightPart).swap(f);}else {    // 量词在内部，需要提到前面string quantf(iter-1, iter+3);   // 保存量词f.erase(iter-1, iter+3);      // 移除量词f.insert(f.begin(), quantf.begin(), quantf.end());return TransformToPNF(f);     // 继续处理}return f;}

5、消去存在量词。

Formula& RemoveEQ(Formula& f)
{set<char> checkedAlpha;FormulaIter eqIter = find(f.begin(), f.end(), EQ);  //找到存在量词的位置if(eqIter == f.end()) return f;FormulaRevIter uqIter = find(FormulaRevIter(eqIter), f.rend(), UQ);  //反向迭代器还要减一// cout<<"我在测试此时的是啥"<<*uqIter<<endl;//debugif(uqIter == f.rend()) { // 该存在量词前没有任意量词char varName = *(eqIter + 1);char newName = GetNewConstantAlha(f);auto rightBound = FindPairChar(eqIter + 3, f.end(), '(', ')');assert(rightBound != f.end());replace(eqIter + 3, rightBound, varName, newName); // 常量化f.erase(eqIter - 1, eqIter + 3);	// 移除存在量词}else {// 记录公式中已经存在的字母，maybecopy_if(f.begin(), f.end(),inserter(checkedAlpha, checkedAlpha.begin()),ptr_fun<int, int>(isalpha));const char oldName = *(eqIter+1);  //eqIter是存在量词的位置，这个得到函数值// 准备任意量词的函数来替换该存在量词const char funcName = FindNewLowerAlpha(checkedAlpha);string funcFormula;funcFormula = funcFormula + funcName+ '(' + *(uqIter-1) + ')';f.erase(eqIter - 1, eqIter + 3);	// 移除存在量词ReplaceAlphaWithString(f, oldName, funcFormula);  //在这里产生替换}// RemoveOuterBracket(f); //这个函数不知道要干啥，感觉没有必要要了，不知道啥含义，我看网上人家也没要return RemoveEQ(f);	// 递归处理
}

6、消去全称量词。

Formula& RemoveUQ(Formula& f)
{FormulaIter uqIter = find(f.begin(), f.end(), UQ);while(uqIter != f.end()) {uqIter = f.erase(uqIter-1, uqIter+3); // 直接移除全称量词uqIter = find(uqIter, f.end(), UQ); // 继续扫描}// RemoveOuterBracket(f); //这个函数不知道要干啥，感觉没有必要要了，不知道啥含义，我看网上人家也没要return f;
}

7、化为Skolem标准型。

Formula& TransformToSkolem(Formula& f)
{RemoveEQ(f);cout<<"6.1消去存在量词："<<endl;cout<<f<<endl; //测试RemoveUQ(f);cout<<"6.2消去全称量词："<<endl;cout<<f<<endl; //测试return f;
}

8、消去合取词，以子句为元素组成一个集合S。

需要考虑子句、子句集的存储结构的设计。

步骤三 选择并设计归结策略，常用的归结策略有：

删除策略、支持集策略、线性归结策略、输入归结策略、单元归结策略、锁归结策略、祖先过滤型策略等。

步骤四 实现归结算法，并在其中实现合一算法，使用归结原理进行定理证明，要求采用归结反演过程，即：

1、先求出要证明的命题公式的否定式的子句集S；

2、然后对子句集S（一次或者多次）使用归结原理；

3、若在某一步推出了空子句，即推出了矛盾，则说明子句集S是不可满足的，从而原否定式也是不可满足的，进而说明原公式是永真的。

合一算法及核心代码如下：

1、置k＝0，Sk＝S， σk ＝ε；

2、若Sk只含有一个谓词公式，则算法停止， σk就是最一般合一；

3、求Sk的差异集Dk；

4、若中存在元素xk和tk ，其中xk是变元， tk是项且xk不在tk中出现，则置Sk ＋1＝Sk{tk/ xk} σk ＝ε然后转Step2；

5、算法停止，S的最一般合一不存在。

Sustitutes MGU(const FormulaNamepace::Subsentence& subsent1,const FormulaNamepace::Subsentence& subsent2){pair<Subsentence, Subsentence> w = { subsent1, subsent2 };Sustitutes mgu;while(w.first != w.second) { // w未合一// 找不一致集auto iter1 = FindPredicate(w.first.begin(), w.first.end());auto iter2 = FindPredicate(w.second.begin(), w.second.end());while(iter1 != w.first.end() && iter2 != w.second.end()) {if(*iter1 != *iter2)break;iter1 = FindPredicate(iter1 + 1, w.first.end());iter2 = FindPredicate(iter2 + 1, w.second.end());}// 找到不一致集合if(iter1 != w.first.end() && iter2 != w.second.end()) {string item1 = GetPredicate(iter1,  w.first.end());string item2 = GetPredicate(iter2,  w.second.end());// 不允许置换有嵌套关系if(StrStr(item1, item2) != item1.end() ||StrStr(item2, item1) != item2.end()) {throw ResolutionException("cannot unifier");}// 只允许常量替换变量if(!IsConstantAlpha(*iter1))item1.swap(item2);// 更新置换，然后置换子句集Sustitutes sustiSet = { make_pair(item1, item2) };mgu = ComposeSustitutes(mgu, sustiSet);Substitution(w.first, mgu);Substitution(w.second, mgu);}else {     // 两子句不可合一throw ResolutionException("cannot unifier");}}return mgu;}

步骤五 编写代码，调试程序。

六、实验要求

根据归结原理编写程序（编程语言不限），要求给出如下过程：

1  求子句集：

         (1) ¬P(x) ÚQ(x)

         (2) ¬P(y) ÚR(y)

         (3)P(a)

         (4)S(a)

         (5) ¬S(z) Ú ¬ R(z)    (¬G)

2  归结:

        (6)R(a)         [(2),(3), σ1={a/y}]

        (7) ¬ R(a)       [(4),(5), σ2 ={a/z}]

        (8)Nil          [(6),(7)]

代码运行结果1
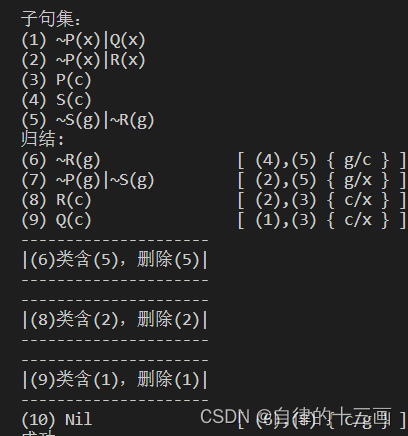
代码运行结果1
水平浸透法+删除策略
                                

 

 

 

代码运行结果2
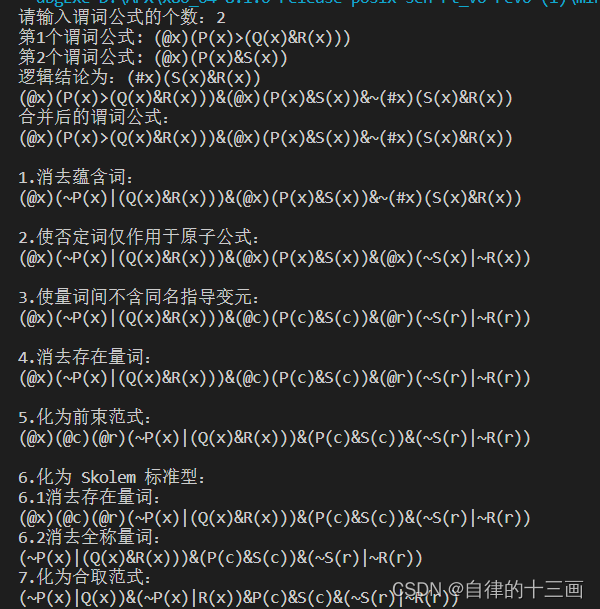
代码运行结果2
支持集策略

 

        该代码是参考了老师给的部分函数以及网上的大佬写的，尽管数据结构等都是仿写，但是自己也将参考的代码都理解了一遍。网上有大佬写的支持集策略，但是有一点点的小bug，比如说在寻找合一的时候不能把本次子句全部遍历完，我在此基础上改善了一下，同时，我也写了水平浸透法+删除策略的归结方法，这个算法也是小缺陷，比如说在删除的时候，目前算法只考虑了删除被别的子句类含的子句，而永真等也应该删除的子句没有去实现，希望接下来会有时间去实现。

        由于很多代码都是参考别的大佬的，所以这里就不粘贴源码出来了。本次实验收获良多。

 

 

 

这篇关于人工智能——基于谓词逻辑的归结原理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/680754。

相关文章

基于人工智能的图像分类系统

基于人工智能的图像分类系统

目录 引言项目背景环境准备 硬件要求软件安装与配置系统设计 系统架构关键技术代码示例 数据预处理模型训练模型预测应用场景结论 1. 引言 图像分类是计算机视觉中的一个重要任务，目标是自动识别图像中的对象类别。通过卷积神经网络（CNN）等深度学习技术，我们可以构建高效的图像分类系统，广泛应用于自动驾驶、医疗影像诊断、监控分析等领域。本文将介绍如何构建一个基于人工智能的图像分类系统，包括环境
阅读更多...
深入探索协同过滤：从原理到推荐模块案例

深入探索协同过滤：从原理到推荐模块案例

文章目录 前言一、协同过滤1. 基于用户的协同过滤（UserCF）2. 基于物品的协同过滤（ItemCF）3. 相似度计算方法 二、相似度计算方法1. 欧氏距离2. 皮尔逊相关系数3. 杰卡德相似系数4. 余弦相似度 三、推荐模块案例1.基于文章的协同过滤推荐功能2.基于用户的协同过滤推荐功能 前言     在信息过载的时代，推荐系统成为连接用户与内容的桥梁。本文聚焦于
阅读更多...
hdu4407(容斥原理)

hdu4407(容斥原理)

题意：给一串数字1,2，......n，两个操作:1、修改第k个数字，2、查询区间[l,r]中与n互质的数之和。 解题思路：咱一看，像线段树，但是如果用线段树做，那么每个区间一定要记录所有的素因子，这样会超内存。然后我就做不来了。后来看了题解，原来是用容斥原理来做的。还记得这道题目吗？求区间[1,r]中与p互质的数的个数，如果不会的话就先去做那题吧。现在这题是求区间[l,r]中与n互质的数的和
阅读更多...
hdu4407容斥原理

hdu4407容斥原理

题意： 有一个元素为 1~n 的数列{An}，有2种操作（1000次）： 1、求某段区间 [a,b] 中与 p 互质的数的和。 2、将数列中某个位置元素的值改变。 import java.io.BufferedInputStream;import java.io.BufferedReader;import java.io.IOException;import java.io.Inpu
阅读更多...
hdu4059容斥原理

hdu4059容斥原理

求1-n中与n互质的数的4次方之和 import java.io.BufferedInputStream;import java.io.BufferedReader;import java.io.IOException;import java.io.InputStream;import java.io.InputStreamReader;import java.io.PrintWrit
阅读更多...
寻迹模块TCRT5000的应用原理和功能实现（基于STM32）

寻迹模块TCRT5000的应用原理和功能实现（基于STM32）

目录 概述 1 认识TCRT5000 1.1 模块介绍 1.2 电气特性 2 系统应用 2.1 系统架构 2.2 STM32Cube创建工程 3 功能实现 3.1 代码实现 3.2 源代码文件 4 功能测试 4.1 检测黑线状态 4.2 未检测黑线状态 概述 本文主要介绍TCRT5000模块的使用原理，包括该模块的硬件实现方式，电路实现原理，还使用STM32类
阅读更多...
基于人工智能的智能家居语音控制系统

基于人工智能的智能家居语音控制系统

目录 引言项目背景环境准备 硬件要求软件安装与配置系统设计 系统架构关键技术代码示例 数据预处理模型训练模型预测应用场景结论 1. 引言 随着物联网（IoT）和人工智能技术的发展，智能家居语音控制系统已经成为现代家庭的一部分。通过语音控制设备，用户可以轻松实现对灯光、空调、门锁等家电的控制，提升生活的便捷性和舒适性。本文将介绍如何构建一个基于人工智能的智能家居语音控制系统，包括环境准备
阅读更多...
TL-Tomcat中长连接的底层源码原理实现

TL-Tomcat中长连接的底层源码原理实现

长连接：浏览器告诉tomcat不要将请求关掉。  如果不是长连接，tomcat响应后会告诉浏览器把这个连接关掉。    tomcat中有一个缓冲区  如果发送大批量数据后 又不处理  那么会堆积缓冲区 后面的请求会越来越慢。
阅读更多...
从希腊神话到好莱坞大片，人工智能的七大历史时期值得铭记

从希腊神话到好莱坞大片，人工智能的七大历史时期值得铭记

本文选自historyextra，机器之心编译出品，参与成员：Angulia、小樱、柒柒、孟婷 你可能听过「技术奇点」，即本世纪某个阶段将出现超级智能，那时，技术将会以人类难以想象的速度飞速发展。同样，黑洞也是一个奇点，在其上任何物理定律都不适用；因此，技术奇点也是超越未来理解范围的一点。 然而，在我们到达那个奇点之前（假设我们能到达），还存在另一个极大的不连续问题，我将它称之
阅读更多...
PHP原理之内存管理中难懂的几个点

PHP原理之内存管理中难懂的几个点

PHP的内存管理, 分为俩大部分, 第一部分是PHP自身的内存管理, 这部分主要的内容就是引用计数, 写时复制, 等等面向应用的层面的管理. 而第二部分就是今天我要介绍的, zend_alloc中描写的关于PHP自身的内存管理, 包括它是如何管理可用内存, 如何分配内存等. 另外, 为什么要写这个呢, 因为之前并没有任何资料来介绍PHP内存管理中使用的策略, 数据结构, 或者算法. 而在我们
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2