鲁宾逊归结原理

子句集中子句之间是合取关系，只要有一个子句不可满足， 则子句集就不可满足。

鲁宾逊归结原理（消解原理）的基本思想：

检查子句集 S 中是否包含空子句，若包含，则 S 不可满足。
若不包含，在 S 中选择合适的子句进行归结，一旦归结出空子句，就说明 S 是不可满足的。

1. 命题逻辑中的归结原理（基子句的归结）

定义3.1（归结）：设C1与C2是子句集中的任意两个子句，如果 C1中的文字L1与 C2中的文字L2互补，那么从C1和 C2中分别消去L1和L2，并将二个子句中余下的部分析取，构成一个新子句C12 。




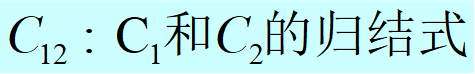
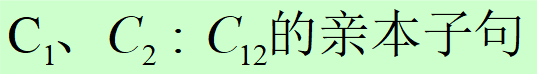
定理3.2：归结式C12是其亲本子句C1与C2的逻辑结论。即如果 C1与C2为真，则C12为真。
推论1：设C1与C2是子句集S中的两个子句，C12是它们的归结式，若用C12代替C1与C2后得到新子句集S1，则由S1不可满足性可推出原子句集S的不可满足性，即：

推论2：设C1与C2是子句集S中的两个子句，C12是它们的归结式，若C12 加入原子句集S，得到新子句集S1，则S与S1在不可满足的意义上是等价的，即：

2. 谓词逻辑中的归结原理（含有变量的子句的归结）

例：





对于谓词逻辑，归结式是其亲本子句的逻辑结论。
对于一阶谓词逻辑，即若子句集是不可满足的，则必存在一个从该子句集到空子句的归结演绎；若从子句集存在一个到空子句的演绎，则该子句集是不可满足的。
如果没有归结出空子句，则既不能说 S 不可满足，也不能说 S 是可满足的。
欢迎大家加我微信交流讨论（请备注csdn上添加）