希尔伯特专题
希尔伯特 包络证明 未出现模态混合现象 是啥?
希尔伯特变换在信号处理中常用于求信号的包络,它是一种线性运算,能够将实数信号转换为其解析信号,即包含原信号及其希尔伯特变换的复数信号。解析信号的实部是原信号,虚部是原信号的希尔伯特变换。 包络证明 在信号处理中,"包络证明"通常指的是使用希尔伯特变换来估计信号的包络的过程,并且在这个过程中没有出现所谓的“模态混合”现象。 希尔伯特变换求包络: 信号的希尔伯特变换可以表示为解析信号的虚部,记作
希尔伯特及其23个著名数学问题
希尔伯特(HilbertD, 1862.1.23~1943.2.14)是二十世纪上半叶德国乃至全世界最伟大的数学家之一。他在横跨两个世纪的六十年的研究生涯中,几乎走遍了现代数学所有前沿阵地,从而把他的思想深深地渗透进了整个现代数学。希尔伯特是哥廷根数学学派的核心,他以其勤奋的工作和真诚的个人品质吸引了来自世界各地的年青学者,使哥廷根的传统在世界产生影响。希尔伯特去世时,德国《自然》杂志发表过这样的
talib.HT_DCPERIOD希尔伯特转换主循环周期
Hilbert Transform希尔伯特转换 关于希尔伯特转换这个大锤,见《初识希尔伯特变换(Hilbert Transform)》 Hilbert Transform - Dominant Cycle Period 此指标由John F. Ehlers发明,在《Rocket Science for Traders: Digital Signal Processing Application
ML(4)-核函数与再生核希尔伯特空间
核函数与再生核希尔伯特空间 1.支持向量积-核函数2.一个函数为核函数的条件3.核函数与希尔伯特空间3.1希尔伯特空间-Hilbert空间 1.支持向量积-核函数 核(kernel)的概念由Aizenman et al.于1964年引入模式识别领域,原文介绍的是势函数的方法。在那之后,核函数在模式识别领域沉积了很久。1992年Boser 等人的在解决支持向量机算法时,重新将核的
ML(4)-核函数与再生核希尔伯特空间
核函数与再生核希尔伯特空间 1.支持向量积-核函数2.一个函数为核函数的条件3.核函数与希尔伯特空间3.1希尔伯特空间-Hilbert空间 1.支持向量积-核函数 核(kernel)的概念由Aizenman et al.于1964年引入模式识别领域,原文介绍的是势函数的方法。在那之后,核函数在模式识别领域沉积了很久。1992年Boser 等人的在解决支持向量机算法时,重新将核的
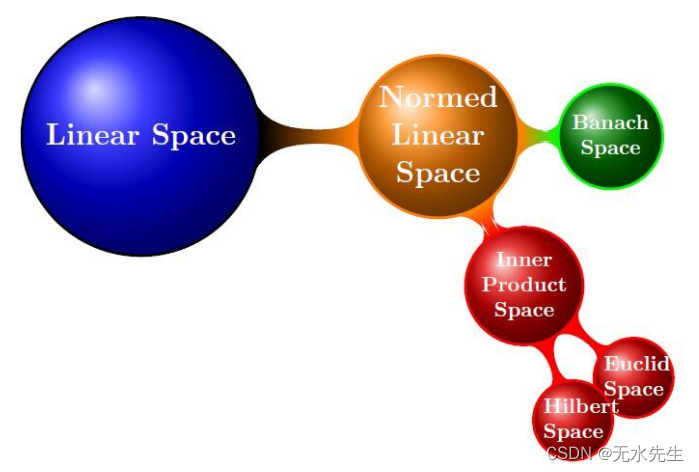
理解数学空间,从距离到希尔伯特空间
在数学中有许多空间表示,比如欧几里德空间、赋范空间、希尔伯特空间等。这些空间之间有什么关系呢? 首先要从距离的定义说起。 什么是距离呢?实际上距离除了我们经常用到的直线距离外,还有向量距离如 Σni=1xi⋅yi−−−−−−−−√ \sqrt{\Sigma_{i=1}^nx_i\cdot y_i}, 函数距离如 ∫ba(f(x)−g(x))2dx \int_a^b(f(x)-g(x))^2d_
希尔伯特变换-matlab仿真
希尔伯特变换(hilbert transform)简介 在信号处理中我们常见的有傅里叶变换,用来分析频域信息,还有拉普拉斯变换和z变换,用于系统分析系统响应。短时傅里叶分析和小波分析用于时频分析。希尔伯特变换似乎听到的比较少。我因为最近在做信号幅度提取的时候看到可以用希尔伯特变换来提取包络,所以才了解到了希尔伯特变换,网上的资料很多,对它的介绍也很多,我对它的了解有限,只是知道它可以做IQ调制,
什么是希尔伯特空间?
照片由 丹·克里斯蒂安·佩杜雷什 on Unsplash 一、说明 在本文中,我们将探讨希尔伯特空间这个非常重要的主题。希尔伯特空间由于其特性而经常出现在物理和工程中。为了理解希尔伯特空间,我们从度量空间的定义开始。 二、基础概念 集合是定义明确的元素的集合。虽然集合本身可能不是很有用,但它们提供了一个非常强大的框架,可以通过笛卡尔积等操作系统
将时间序列转成图像——希尔伯特-黄变换方法 Matlab实现
目录 1 方法 2 Matlab代码实现 3 结果 【若觉文章质量良好且有用,请别忘了点赞收藏加关注,这将是我继续分享的动力,万分感谢!】 其他: 1.时间序列转二维图像方法及其应用研究综述_vm-1215的博客-CSDN博客 2.将时间序列转成图像——短时傅里叶方法 Matlab实现_vm-1215的博客-CSDN博客 3.将时间序列转成图像——小波变换方法 Matlab实现
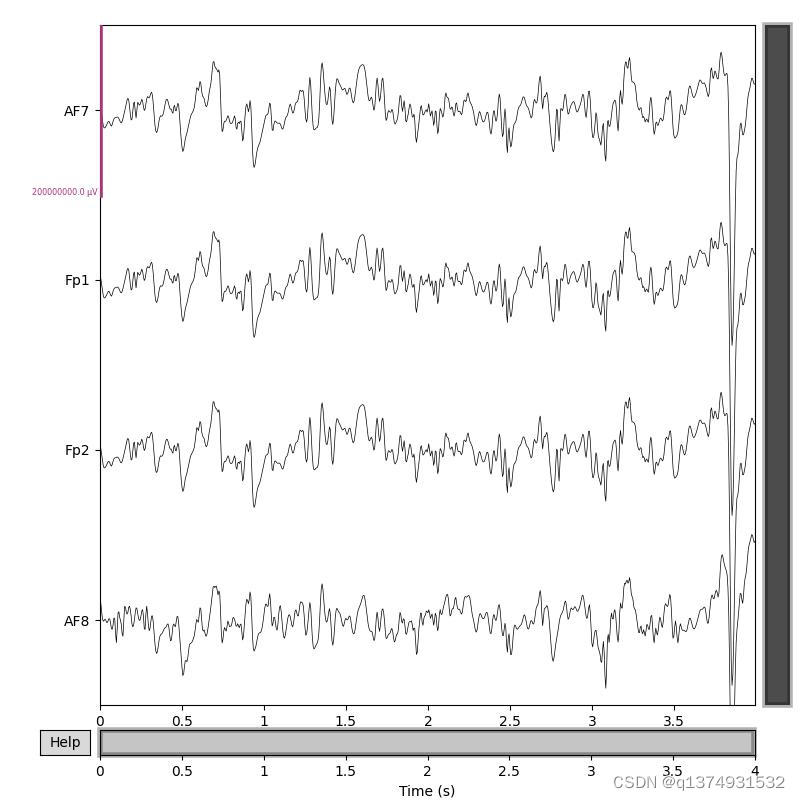
基于经验模态分解和希尔伯特变换(EMD-HHT)去除脑电图中的高频噪声
EMD是一种常用于处理非平稳信号的方法。可以将一段时间信号分解为不同频率的本征函数(IFM)从而进行频率分析。根据Ahmet Mert等人的论文,我自动去除了混杂在脑电信号中的高频噪声。并且对于噪声很小的片段,不会破坏原信号。 过滤前 过滤后