【题目来源】https://www.acwing.com/problem/content/850/【问题描述】 给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。 请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。 若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑

邻接矩阵 我们定义一个数组a[MAXN][MAXN]; 那么存图方式就是： a[i][j]=val; 对于无向图，就代表i和j之间有一条权值为val的边，如果是 无权图，val=1。 对于有向图，就代表i->j（j->i你不清楚）有一条权值 为val的边，无权图的话val=1。 这样我们就能够用这样一个矩阵实现了图的存放，但是，如果点 的数量过大了怎么办呢？二维数组可是开不了很大的啊。比如 有

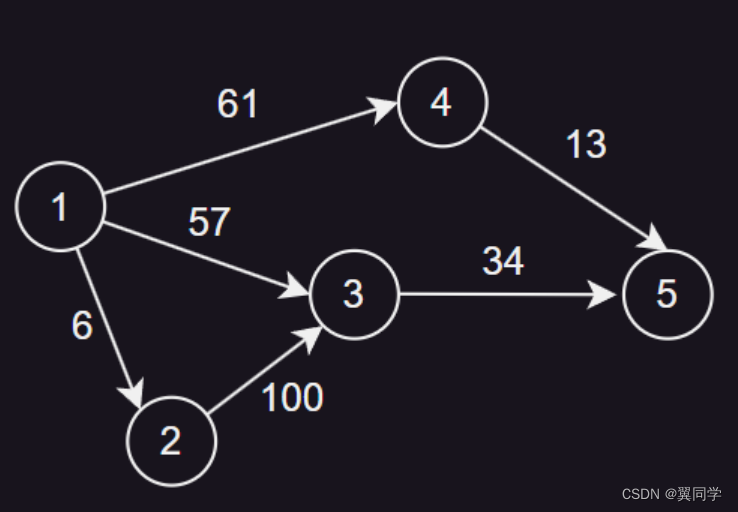
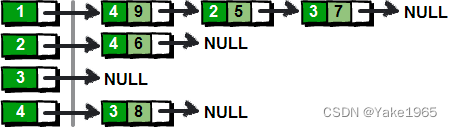
一、概述 链式前向星是一种用于存储图的数据结构，特别适合于存储稀疏图，它可以有效地存储图的边和节点信息，以及边的权重。 它的主要思想是将每个节点的所有出边存储在一起，通过数组的方式连接（类似静态数组实现链表）。这种方法的优点是存储空间小，查询速度快，尤其适合于处理大规模的图数据，在一些笔试或者竞赛的场景中经常使用。 下面，我们用这张图来图解一下链式前向星的存储逻辑： 二、前置准备

【题目描述】 请编程输出无向无权图各个顶点的度。【测试样例示意图】【算法代码】 #include <bits/stdc++.h>using namespace std;const int maxn=100;int mp[maxn][maxn]; //无向无权图的邻接矩阵int V,E; //顶点数、边数int sx,ex; //起点编号、终点编号int main() {cin>>V>>

图最常见的两种存储方式是邻接表和邻接矩阵。 链式前向星其实就是静态建立的邻接表，时间效率为 O(n)，空间效率也为 O(n)。遍历效率也为 O(n)。 一、邻接表 邻接表存储方式适合存储边稀疏的图，判断两点之间是否有边不方便； 邻接矩阵适合存储边稠密的，判断边和权值都很方便。 邻接表的逻辑结构： 主要有两个部分组成： 1）顶点数组； 2）顶点所邻的边形成的链表【所以叫“邻接表” = 邻

我有一个图像采集软件，开始采集后，主线程会不断地接收到图像回调，然后每接收到一张图像数据，就通知业务线程保存该图像到本地文件。 但是实际运行的时候发现，可能是由于业务线程存图的操作占用资源，会导致主线程接收图像会有卡顿，或者丢图，然后存的图也有些异常图像（比如下一张图的某一部分覆盖到上一张图上）。 估计就是业务线程QImage::save保存图像这一操作，比较耗费资源，同时会与主线程抢占资源吧

每日一题做题记录，参考官方和三叶的题解 目录 题目要求思路：BFSJava链式前向星 C++ 总结 题目要求 思路：BFS 由题目可知，服务器实际构成一张无向图，所以想到BFS方式预处理出一个distance数组，表示各节点到0号点的最短距离。 各节点与0号距离为 d i s t dist dist，则发送消息立刻收到回复的时间至少为 t i m e = d i s t

C--最短路 Time Limit: 7000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Problem Description 给出一个带权无向图，包含n个点，m条边。求出s，e的最短路。保证最短路存在。 Input  多组输入。 对于每组数据。 第一行输入n，m(1<= n && n<=5*10^5,1 <= m &