本文主要是介绍存图方式【知识点】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
邻接矩阵
我们定义一个数组a[MAXN][MAXN]; 那么存图方式就是:
a[i][j]=val;
对于无向图,就代表i和j之间有一条权值为val的边,如果是
无权图,val=1。
对于有向图,就代表i->j(j->i你不清楚)有一条权值
为val的边,无权图的话val=1。
这样我们就能够用这样一个矩阵实现了图的存放,但是,如果点
的数量过大了怎么办呢?二维数组可是开不了很大的啊。比如
有50000个点。那么二位数组就存放不下了,那么我们就要借助
邻接表法了。
邻接表法
大家在前期的时候学STL的时候学过vector,而邻接表就是
用vector来进行存放的
代码实现(以无向图为例)
vector <int > e[ MAXN ]; // edge
vector <int > v[ MAXN ]; // val
cin >>a>>b>>c;
e[a]. push_back (b);
v[a]. push_back (c);
e[b]. push_back (a);
v[b]. push_back (c);
前向星.
前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,
并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.
用len[i]来记录所有以i为起点的边在数组中的存储长度.
用head[i]记录以i为边集在数组中的第一个存储位置.
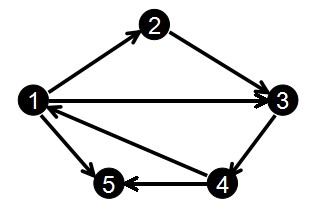
那么对于下图:
我们输入边的顺序为:
1 2
2 3
3 4
1 3
4 1
1 5
4 5
那么排完序后就得到:
编号: 1 2 3 4 5 6 7
起点u: 1 1 1 2 3 4 4
终点v: 2 3 5 3 4 1 5
得到:
head[1] = 1 len[1] = 3
head[2] = 4 len[2] = 1
head[3] = 5 len[3] = 1
head[4] = 6 len[4] = 2
但是利用前向星会有排序操作,如果用快排时间至少为O(nlog(n))
链式前向星
我们用head[i]表示以i为起点的最后一条边的储存位置,
next[i]表示与第i条边同起点的上一条边的储存位置,e[i]表
示第i条边的终点。
我们输入边的顺序为:
1 2
2 3
3 4
1 3
4 1
1 5
4 5
加边
struct Edge
{
int next ;
int e;
int w;
} edge [ MAXN ];edge[i].next表示同起点的上一条边,edge[i].e代表这条边的终点,
edge[i].w为权值。void add (int u,int v,int w)
{
edge [cnt ].w = w;
edge [cnt ]. to = v;
edge [cnt ]. next = head [u];
head [u] = cnt ++;
}
cnt初始化为0,head初始化为-1。边的遍历,遍历以u为起点的所有边
for (int i= head [u];~i;i= edge [i]. next )
{
cout <<u<<" ->" <<edge [i].e<< endl ;
}
倒序遍历#include<bits/stdc++.h>
using namespace std;
#define MAXN 10050
struct EDGE
{int w;//权值 int next;//与该边同起点的上一条边的位置 int e;//边的终点
}edge[MAXN];
int cnt;
int head[MAXN];//以i为起点的最后一条边
void add(int u,int v,int w)
{edge[cnt].w=w;edge[cnt].e=v;edge[cnt].next=head[u];head[u]=cnt++;
} int main()
{memset(head,0,sizeof(head));cnt=1;int n,a,b,c;cin>>n;for(int i=1;i<=n;i++){cin>>a>>b>>c;add(a,b,c);}int start;cin>>start;for(int i=head[start];i!=0;i=edge[i].next){cout<<start<<"->"<<edge[i].e<<" "<<edge[i].w<<endl;}return 0;
}
这篇关于存图方式【知识点】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!