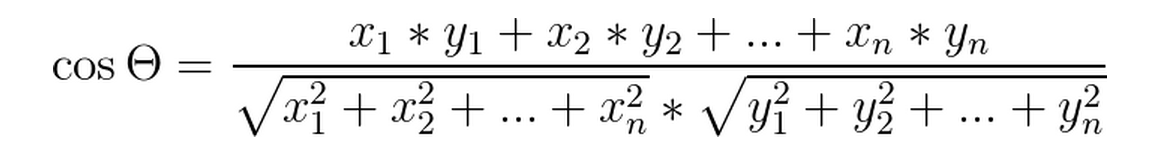夹角专题
OpenCV:已知三角形的两边 求夹角的问题(余弦定理)
// 找余弦角度: 线段pt0-pt1 和线段 pt0-pt2: double angle( Point pt1, Point pt2, Point pt0 ) { double dx1 = pt1.x - pt0.x; double dy1 = pt1.y - pt0.y; double dx2 = pt2.x - pt0.x; double dy2 = pt2.y - pt0.
HDU2076 夹角有多大(题目已修改,注意读题)【水题】【计算几何】
夹角有多大(题目已修改,注意读题) Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 10194 Accepted Submission(s): 4072 Problem Descr
[Unity 3D] 求两个向量间的夹角的方法
1、 Vector3 d1 = transform.forward; Vector3 d2 = new Vector3(0,3,0); float angle = Vector3.Angle(d1, d2); 2、 Vector3 d1 = transform.forward; Vector3 d2 = new Vector3(0,3,0); float dot = Vector3.Dot(d1,
java 三点求角度_求给定三个点的夹角
求给定三个点的夹角,其实是求$$$$两个向量之间的夹角$$\alpha$$。本文采用如下公式求解。 $$\cos{\alpha}=\frac{{A}\times{B}}{\|A\|\|B\|}$$ 源代码如下: double getAngleByThreeP(double pointx[3], double pointy[3]) { double a_b_x = pointx[0] - poin
hdu2080 夹角有多大Ⅱ
设:原点O坐标(0,0),向量A坐标(x1,y1),向量B坐标(x2,y2),直线OA与OB的夹角度数等于 α; 由向量的数量积公式: A · B = |A| * |B| * cosα 所以: cosα =
POJ Space Ant (向量夹角)
http://poj.org/problem?id=1696 水。求出最大余弦值即可。 完整代码: /*0ms,548KB*/#include<cstdio>#include<cstring>#include<cmath>double x[55], y[55], dx, dy;bool vis[55];///单位化向量inline void dentity_vecto
Python根据3个点确定两个向量之间的夹角-180度到180方向进行矫正
import cv2 import numpy as np # 读取图片 image = cv2.imread(r'D:\dmp\cat.jpg') height, width = image.shape[:2] # 定义三个定位点(这里假设是图片上的坐标),分别表示原点,向量1终点,向量2终点,下例表示顺时针90度pts1 = np.float32([[100, 100], [
11、基于ROS的通过计算夹角实现点云中的地面部分提取
基于ROS的通过计算夹角实现点云中的地面部分提取 一、理论基础 首先将整个点云中的地面部分提取出来,这能有效减少点云数量,减少后面的聚类开销。采用激光扫描到障碍物和地面的夹角不同的原理进行提取,具体如下: 激光扫描到地面点障碍物点判断示意图情况下所示: 激光未扫描到障碍物地面点时候,θ角很小(地面有一点坡道),甚至为0(平坦地面),激光未扫描到地面障碍物点示意图如下: 两个相邻激光线
求两个向量之间的夹角
求两个向量之间的夹角 介绍Unity的API求向量夹角Vector3.AngleVector3.SignedAngle 自定义获取方法0-360度的夹角 总结 介绍 求两个向量之间的夹角方法有很多,比如说Unity中的Vector3.Angle,Vector3.SignedAngle等方法,具体在什么情况下使用这个还是得看这几个函数的结果是什么。 Unity的API求向量夹角
计算2个空间向量支架的夹角(固定系欧拉角XYZ)分量
前提:固定系欧拉角,旋转顺序XYZ 直接用py文件简单计算: from scipy.spatial.transform import Rotationimport numpy as npdef calculate_euler_angles(vec1, vec2, rotation_order='xyz'):# 将法向量转换为单位向量vec1_normalized = vec1 / np.
为什么两个向量的内积等于模长乘夹角?
为什么两个向量的内积等于模长乘夹角? 已知两个向量 a = [ a 1 , a 2 ] a=[a_1,a_2] a=[a1,a2]和 b = [ b 1 , b 2 ] b=[b_1,b_2] b=[b1,b2],他们的内积为 a b = a 1 b 1 + a 2 b 2 ab=a_1b_1+a_2b_2 ab=a1b1+a2b2,看书上的定义该内积的值是一个
透视投影中已知两平面的单应矩阵,能否求出这两平面的夹角?
转载:https://www.zhihu.com/question/46805492 透视投影中已知两平面的单应矩阵,能否求出这两平面的夹角?修改 如下图透视投影的例子,已知两个平面上对应点的单应矩阵且两平面上对应点的连线交于O点,能否求出两平面在空间中的夹角? 补充一下条件:已知点O到平面π‘的距离及点O在平面π’上的投影点,投影方向为平面π’的法线方向,即已知成像平面为x'o
【CV】计算两个向量的夹角,并使用 OpenCV 可视化弧线
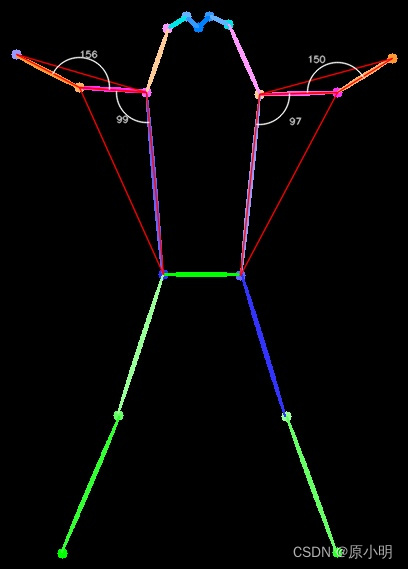
背景 基于人体/动物,骨骼点数据,计算关节角度 1. 原理 计算两个向量的夹角,我们已三个点为例,BA 向量和BC向量,求 B 的角度。若为四个点,延长交叉即可。 2. 效果 效果图如下 3. 核心代码 def compute_vector_angle(a, b, c):"""计算两个向量 ba 和 bc 向量的夹角@params a , 点 a@params b , 点 b@
欧氏距离,曼哈顿距离,夹角余弦距离,切比雪夫距离,汉明距离,闵可夫斯基距离,马氏距离
目录 1.欧式距离EuclideanDistance 2. 曼哈顿距离(ManhattanDistance) 3. 夹角余弦 4.汉明距离(Hamming Distance) 1.欧式距离EuclideanDistance 欧式距离:也称欧几里得距离,在一个N维度的空间里,求两个点的距离,这个距离肯定是一个大于等于零的数字,那么这个距离需要用两个点在各自维度上的坐标
求两个(法)向量之间的rpy夹角
主要使用Eigen库实现: 1. 四元素到欧拉角的转换 #include <array>#include <Eigen/Geometry>template <typename T>inline Eigen::Matrix<typename std::remove_reference<T>::type::Scalar, 3, 1> eulerAnglesZYX(T q_in){type
基于夹角余弦计算轨迹相似度
目录 背景预备知识算法流程图核心代码优缺点 背景 同一个司机同一辆车跑同一个运单,结果来自中交兴路定位和来自手机app的定位画出的两条轨迹形同陌路,有时候你会觉得就是一车辆在不同时间的位置,几乎在一条曲线上,如图1所示,有时候你又会觉得根本就是两辆车的轨迹,如图2所示,来自中交兴路和手机app的两者轨迹是否存在亲近关系呢?如果存在,亲近关系又是多少?该如何科学合理度量? 图


![[Unity 3D] 求两个向量间的夹角的方法](/front/images/it_default2.jpg)