埃氏专题
求素数的几个方法(最朴素版、n*sqrt(n)版、埃氏筛、欧拉筛)
最朴素版O(n^2) #include <bits/stdc++.h>using namespace std;int n, cnt, prim[6000000];bool flag; //true 表示质数int main(){scanf("%d", &n);for(int i=2; i<=n; ++i){flag=true; //默认为质数for(int j=2; j<=i-
Python 埃氏筛法
# -*- coding: utf-8 -*-# filter()也接收一个函数和一个序列。和map()不同的是,filter()把传入的函数依次作用于每个元素,然后根据返回值是True还是False决定保留还是丢弃该元素。# 构造一个奇数序列,排除了所有偶数,因为除了2之外的偶数都是非素数def _odd_iter():a = 1while True:a = a + 2yield a #
数学题目系列(一)|丑数|各位和|埃氏筛|欧拉筛
一.丑数 链接:丑数 分析: 丑数只有2,3,5这三个质因数,num = 2a + 3b + 5c也就是一个丑数是由若干个2,3,5组成,那么丑数除以这若干个数字最后一定变为1 代码 class Solution {public boolean isUgly(int n) {if (n <= 0) return false;int[] factors = { 2, 3, 5 };for
《算法笔记》系列----质数的判断(埃氏筛法)
目录 一、朴素算法 二、埃氏筛法 1、与朴素算法对比 2、算法介绍 3、例题即代码实现 一、朴素算法 从素数的定义中可以知道,一个整数n要被判断为素数,需要判断n是否能被2.3.n- 1中的一个整除。只2,3..n- 1都不能整除n,n才能判定为素数,而只要有一个能整除n的数出现,n就可以判定为非素数。 这样的判定方法没有问题,复杂度为0(
埃氏筛选法---打印素数表
思想:算法从小到大枚举所有数,对于每一个素数,筛去它的所有倍数,剩下的就是素数 对于n在10^5以内的可以使用isPrime()进行判断,但是对于需要更大范围的素数表,可以使用该方法 代码核心实现 //素数筛选法代码const int maxn=101;//表长int prime[maxn],num;//prime数组 存放所有的素数,num为素数个数bool p[maxn]={0
【No.20】蓝桥杯简单数论下|寻找整数|素数的判断|笨小猴|最大最小公倍数|素数筛|埃氏筛|欧氏线性筛|质数|分解质因子(C++)
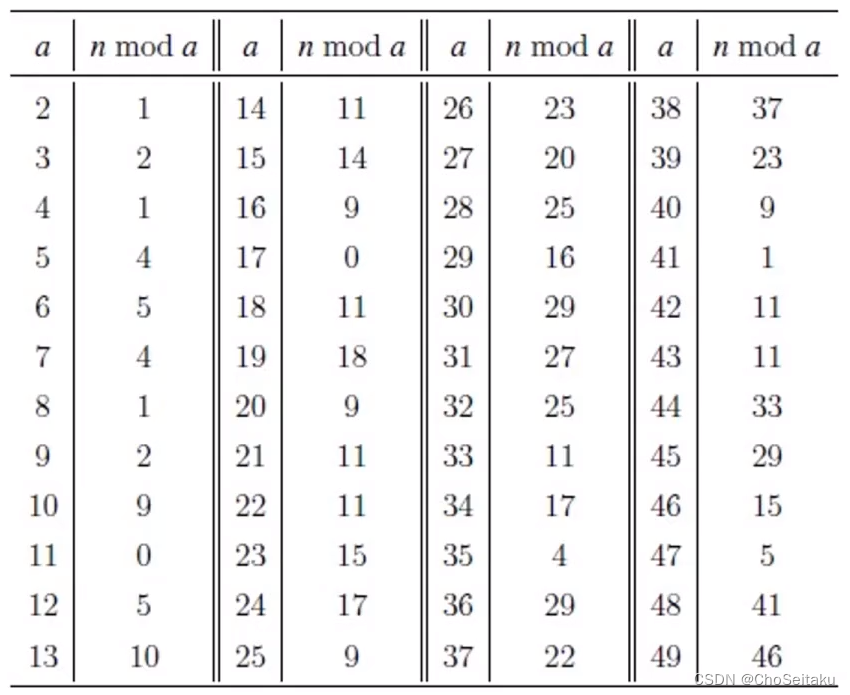
寻找整数 【题目描述】 有一个不超过 1 0 1 7 10^17 1017的正整数n,知道这个数除以2至49后的余数如下表所示,求这个正整数最小是多少 解法一:模拟 暴力法:一个个检验 1 … 1 0 17 1\dots 10^{17} 1…1017的每个数 由于这个数n最大可能是 1 0 17 10^{17} 1017,验证的时间太长 解法二:LCM 从表格的第一个数2开始,逐个增加
【中国大学MOOC】java程序设计-week3-用“埃氏筛法”求2~100以内的素数
1.题目 用“埃氏筛法”求2~100以内的素数。2~100以内的数,先去掉2的倍数,再去掉3的倍数,再去掉5的倍数,……依此类推,最后剩下的就是素数。 要求使用数组及增强的for语句。 提示:可以使用一个boolean类型的数组,所以“将某个数i去掉”,可以表示成a[i]=false。当然也可以使用其他方法。 请注意代码风格:类名、变量名的命名,以及必要注释等等; 评分标准: 使用了数组
素数算法(普通求解,埃氏筛,欧拉筛)
素数算法(常规求解,埃氏筛,欧拉筛) 1. 常规求解1.1 原理解释1.2 算法实现 2 . 埃氏筛2.1 原理解释2.2 算法实现 3. 欧拉筛3.1 原理解释3.2 算法实现 1. 常规求解 1.1 原理解释 枚举法是一种简单的求解素数的方法,其基本思想是从2开始逐个判断每个数字是否为素数。具体来说,对于一个待判断的数n,我们可以从2开始依次尝试将n除以小于等于n的开方的
#埃氏筛,欧拉函数#洛谷 3601 签到题
题目 求 ∑ i = l r i − φ ( i ) \sum_{i=l}^{r}i-\varphi(i) i=l∑ri−φ(i) 分析 首先这道题数据范围非常大,杜教筛是不可能的,所以只能用 r − l ≤ 1 0 6 r-l\leq10^6 r−l≤106这一条件,那么首先预处理 1 0 6 10^6 106以内的质数,然后用这些质数求欧拉函数,对于大质数,当然是用另外一个数组记录
埃氏筛欧拉筛区间筛笔记
//埃氏筛#include<iostream>#include<cstdio>#include<vector>#include<cstring>using namespace std;const int maxn =1e7+10;vector<int> primes;//存放素数的不定长数组bool judge[maxn]; //筛除判断int main(){int i;memse
求n以内的的素数——埃氏筛法和欧拉筛法
求N以内的素数,朴素算法对于10^7之类的大数无疑是要超时的。时间复杂度为O(N^2)和O(N) 所以就需要一个效率更加高的方法来进行素数筛选。 1.Eratosthenes筛法(埃氏筛法) 时间复杂度:O(n*lglgn)( 约等于 O(n*1.5) ) 筛法的思想:对于不超过N的每个非负整数p,删除2p,3p,4p,...,但处理完所有数之后,还没有被删除的就是素数。可用标志数组bk
868. 筛质数 Java题解 (埃氏筛,线性筛)
输入样例: 8 输出样例: 4 解题思路: 埃氏筛质数:又叫朴素筛法,求某个区间的质数个数时,从2开始,将每个数的倍数都筛掉,剩下的数就是质数。缺点:会对某个数重复筛。时间复杂度为O(nlogn) 线性筛法:对埃氏筛的优化,埃氏筛的任意一个数都被它的因数筛了一遍,实际上只需要筛一次就行,即每次只用最小质因子筛,不会被重复筛,时间复杂度为O(nloglogn),非常接近线性
埃氏筛法,快速求出n范围内的素数个数
如果要求一个数是不是素数,只要求2到√n就行,时间复杂度O(√n)。 但是如果判断多个数字是不是素数,如果还用这种方法的话,就会有许多重复判断的。比如,2是素数,那么4,6,8,10等等,全都不是素数了。因此我们只要知道了2是素数后,就把所有2的倍数给去掉,不用在判断了,然后接下来碰到的最小的数字肯定是一个素数,这就是埃氏筛法。 如图, 把2的倍数去掉后,碰到的是3,三肯定是素数,然后把3的倍
找质数(枚举 埃氏筛 线性筛)
输入一个数,返回小于等于这个数的质数。 枚举法: public static int countPrimes(int n) {int cnt=0;for(int i=2;i<n;i++) {if(prime(i))cnt++;}return cnt;}private static boolean prime(int x) {for(int i=2;i*i<=x;i++){if(x%i=