用t-SNE可视化特征，查看特征的可分性 t-SNE是一个很好的可视化工具，这里备份一个用t-SNE可视化特征的例子，以便今后有需要查询使用 import numpy as npimport matplotlib.pyplot as pltimport jsonfrom sklearn import manifold%matplotlib inlinedef draw_

可分拓扑空间 如果拓扑空间有可数的稠密子集，则称是可分拓扑空间。 可分：有可数子集A， 拓扑空间： 1.， 2.任意并 3.有限交    稠密： 闭包 导集：所有聚点的集合 聚点：任意去心领域， 例1 余有限拓扑可分 是可分的拓扑空间  余有限拓扑, complement+finite=cof 可分有可数的稠密子集有可数子集A， 证明

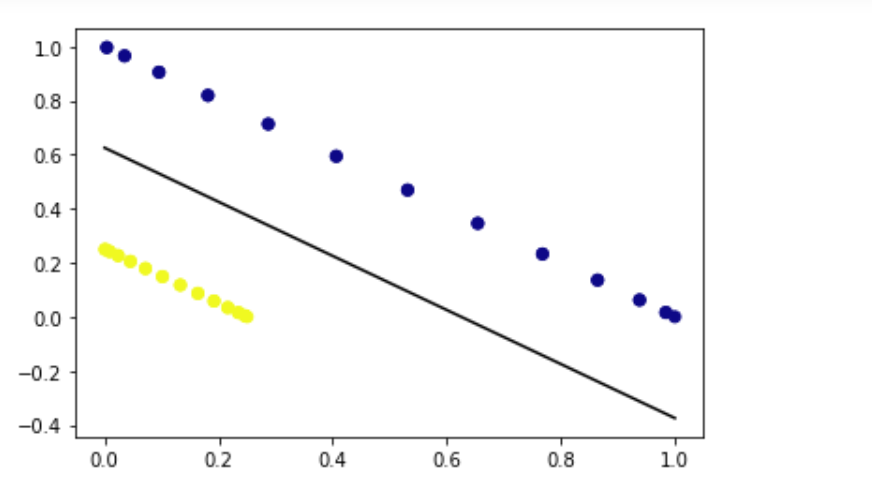
线性可分性是指二分类问题中的数据点可以用线性决策边界分离。如果数据点可以使用线、线性函数或平坦超平面来分离，则认为是线性可分离的。 线性可分性是神经网络中的一个重要概念。如果n维空间中的分离点遵循 则它被称为线性可分的。 对于二维输入，如果存在一条线（其方程为 ）将一个类别的所有样本与另一个类别分开。这样的分类问题被称为“线性可分离”，即通过i/p的线性组合进行分离。 数学中的线性可