本文主要是介绍Python中的线性可分性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
线性可分性是指二分类问题中的数据点可以用线性决策边界分离。如果数据点可以使用线、线性函数或平坦超平面来分离,则认为是线性可分离的。
-
线性可分性是神经网络中的一个重要概念。如果n维空间中的分离点遵循

则它被称为线性可分的。 -
对于二维输入,如果存在一条线(其方程为
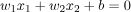
)将一个类别的所有样本与另一个类别分开。这样的分类问题被称为“线性可分离”,即通过i/p的线性组合进行分离。
数学中的线性可分
线性可分性是在线性代数和最优化理论的背景下引入的。它谈到了超平面在高维空间中划分两类数据点的能力。
让我们使用p维空间中的一组数据点的例子,其中p是每个点必须表征它的特征或变量的数量。
线性函数
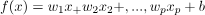
可以用来表示超平面,其中
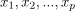
是数据点的特征,
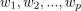
是相应的权重。所以我们可以用一条直线把两个不同的类别分开,并把它们表示在图上,那么我们就说它是线性可分的,条件是它应该是y = ax + b的形式,x的幂应该是1,只有这样我们才能线性地把它们分开。
由于许多分类技术依赖于线性可分性假设,线性可分性是机器学习中的一个关键思想。
检查线性可分性的方法
- 目视检查:如果不同的直线或平面划分了不同的组,则可以通过在2D或3D空间中绘制数据点来进行视觉检查。如果可以看到这样的边界,则数据可以是线性可分的。
- 感知器学习算法:这种二元线性分类器通过迭代学习分离超平面将输入分为两类。如果该方法找到分离超平面并收敛,则数据是线性可分的。否则,那就不是。
- 支持向量机:支持向量机是一种很受欢迎的分类技术,可以处理可以线性分离的数据。为了优化两个类之间的间隔,他们确定了分离超平面。如果裕度大于零,则数据可以线性分离。
- 内核方法:使用这一系列技术可以将数据转换到更高维的空间中,在那里它可能是线性可分的。如果转换数据是线性可分的,则原始数据也是线性可分的。
- 二次规划:找到减少分类误差的分离超平面可以使用二次规划来完成。如果找到解,则数据可以线性分离。
在真实的世界中,数据点通常不是完全线性可分的,因此有时我们使用更先进的技术来使数据点线性可分。
将非线性数据转换为线性数据的方法
可以使用许多技术将非线性可分离数据转换为线性可分离数据。如果样本不是线性可分的,即没有直线可以将属于两个类别的样本分开,那么就不可能有任何简单的感知来完成分类任务。
以下是一些典型的策略:
- 多项式特征:当添加多项式特征时,将非线性可分离数据转换为线性可分离数据很简单。决策边界可以通过包括高阶多项式分量而变得更加灵活和非线性,并且数据可以在改变的特征空间中变得线性可分。
- 核方法:使用核方法,数据可以在高维空间中线性分离,可以将数据转换到该空间中。将核方法与支持向量机(SVM)相结合,可以在转换后的空间中学习线性决策边界。
- 神经网络:神经网络是有效的模型,可以学习复杂的非线性输入输出映射。我们可以学习一个非线性的决策边界,通过使用神经网络中更多的隐藏层来训练非线性可分离的数据来对数据进行分类。
- 流形学习:找到非线性可分离数据的底层结构可以通过流形学习来完成,这是一种无监督学习。也许可以通过识别数据所在的流形将数据转换到一个更高维的空间,在那里它是线性可分的。
实践案例
检查线性可分性
from sklearn import svm
import numpy as np # Making dataset
X = np.array([[1, 2], [2, 3], [3, 1], [4, 3]])
Y = np.array([0, 0, 1, 1]) # Now lets train svm model
model = svm.SVC(kernel='linear')
model.fit(X, Y) # Lets predict for new input
n_data = np.array([[5, 2], [2, 1]])
pred = model.predict(n_data)
print(pred)
输出
[1 0]
我们来画出这个决策边界
import matplotlib.pyplot as plt # lets plot decision boundary for this
w = model.coef_[0]
b = model.intercept_[0]
x = np.linspace(1, 4)
y = -(w[0] / w[1]) * x - b / w[1]
plt.plot(x, y, 'k-') # plot data points
plt.scatter(X[:, 0], X[:, 1], c=Y)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()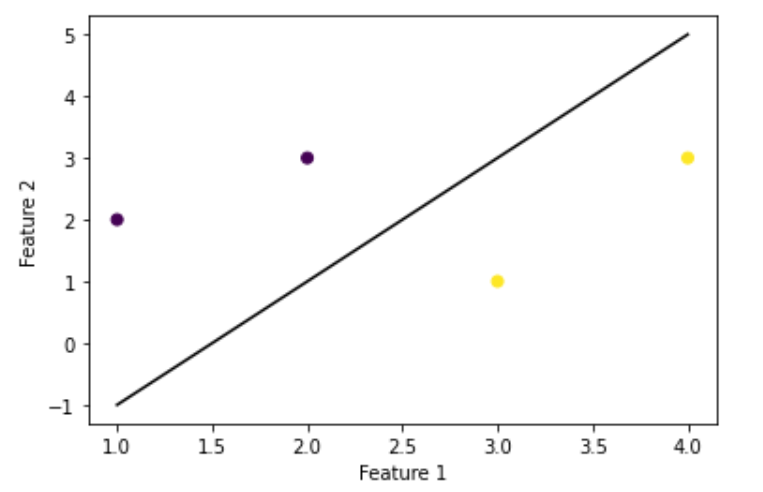
将不可分离数据转换为可分离数据
from sklearn.datasets import make_circles
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np # first lets create non-linear dataset
x_val, y_val = make_circles(n_samples=50, factor=0.5) # Now lets plot and see our dataset
plt.scatter(x_val[:, 0], x_val[:, 1], c=y_val, cmap='plasma')
plt.show() 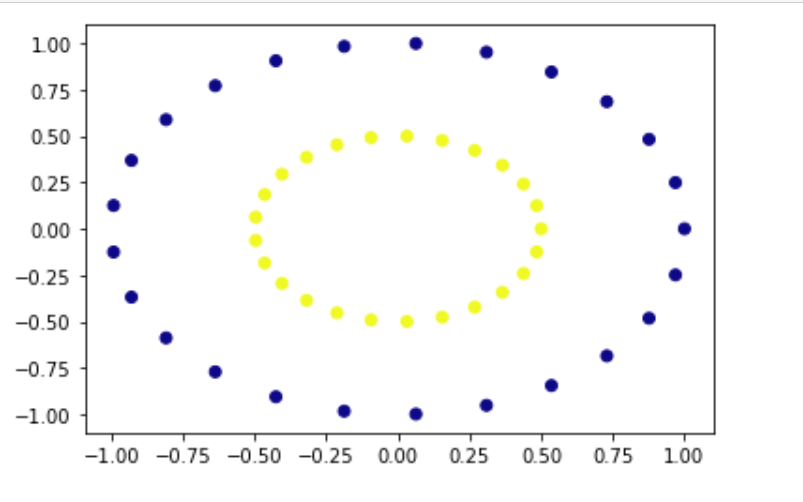
应用核技巧将数据映射到高维空间
# apply kernel trick to map data into higher-dimensional space
x_new = np.vstack((x_val[:, 0]**2, x_val[:, 1]**2)).T # Now fit SVM on mapped data
svm = SVC(kernel='linear')
svm.fit(x_new, y_val) # plot decision boundary in mapped space
w = svm.coef_
a = -w[0][0] / w[0][1]
x = np.linspace(0, 1)
y = a * x - (svm.intercept_[0]) / w[0][1]
plt.plot(x, y, 'k-') # plot mapped data
plt.scatter(x_new[:, 0], x_new[:, 1], c=y_val, cmap='plasma')
plt.show() 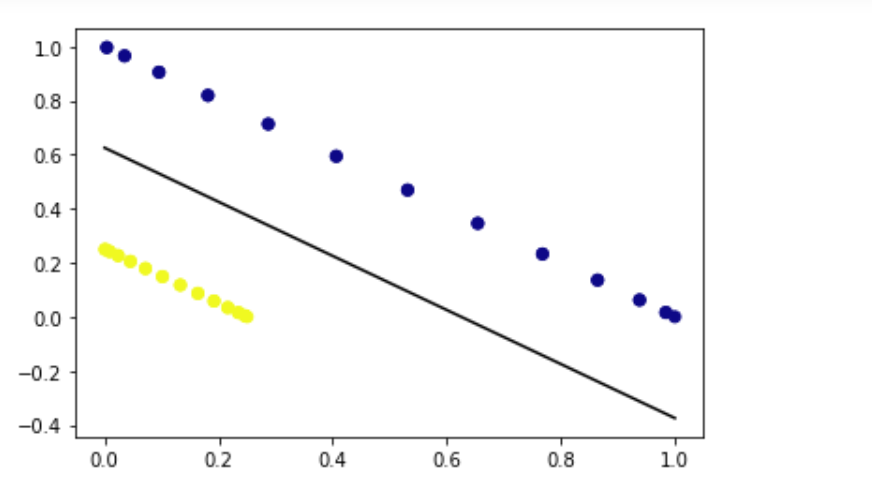
这篇关于Python中的线性可分性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







