取余专题
ASP.NET MVC企业级程序设计(增删,int类型转时间取余)
目录 题目: 实现过程 控制器代码 DAL BLL Index Jia 题目: 实现过程 控制器代码 using System;using System.Collections.Generic;using System.Linq;using System.Web;using System.Web.Mvc;using MvcA
PHP中余数、取余的妙用
转自:http://www.jb51.net/article/68567.htm 这篇文章主要介绍了PHP中余数、取余的妙用,这个是在WEB开发中一个经常使用的小技巧,不管是在表格、ul、li或者是换行等HTML处理中,需要隔几行换行,隔几行加入ul或li的结束标记等时候,特别的有用,需要的朋友可以参考下 <?php$ary=array("name","egineer","sonny"
关于与运算和取余之间的关系
一个数和3进行与运算,就是对4取余. 解释: 和3进行与运算,是取该数2进制形式的最后2位的值,因为3的二进制形式是(假设该数用1个字节表示,多个字节也一样,这里为了讲述,暂举1个字节为例)00000011,最后两位和1进行与,则把该数最后2位的状态取出来(和1与的特性,不理解的话复习数字逻辑基础).如下推导: 随便举一个数255,其二进制形式是11111111,根据十进制和二进制之间的转
【ETOJ P1023】同鱼系 题解(数学+取余)
题目描述 给定一个大小为 n n n 的数组 a a a 和一个整数 k k k。 你可以执行以下操作任意次(0次也行): 选择一个下标 i i i 满足 1 ≤ i ≤ n − k 1 \leq i \leq n-k 1≤i≤n−k,然后交换 a i a_i ai 和 a i + k a_{i+k} ai+k。 问是否可以使得数组变为非降序。 输入格式 第一行两个整
代码优化---取余(%)优化
为了进一步优化程序代码,经常要对除法,浮点等运算进行优化,这里给出整形变量之间%计算的优化: f(x,y) = x%y; 优化如下: f(x,y) = x - y * (x/y); 写成函数如下: int MOD(int x, int y){return x - y * (x / y);};
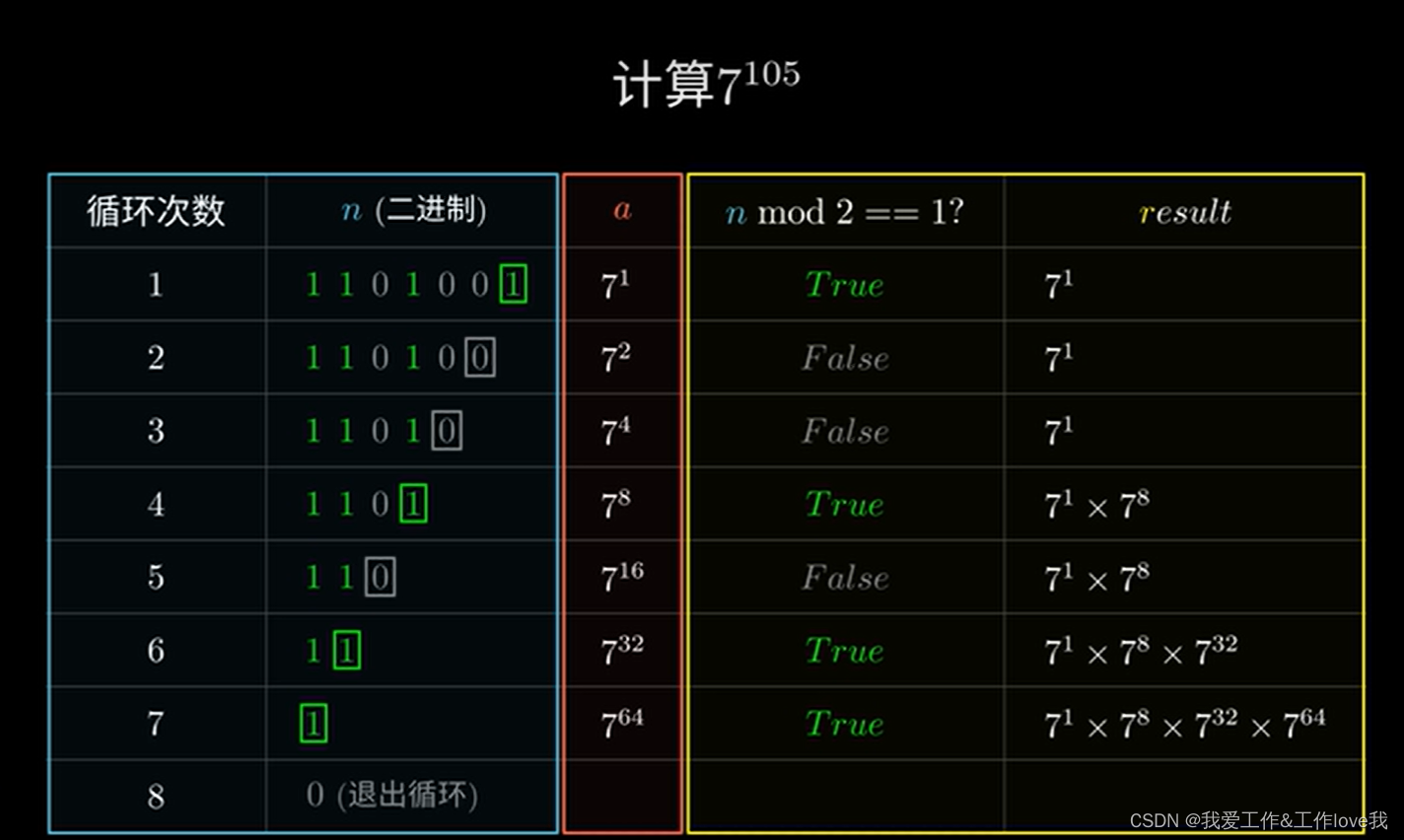
快速幂-计算a的b次对m取余
题目 题解参考 a = a ∗ a a = a*a a=a∗a这部分是计算 a 2 i a^{2^i} a2i, a b = Π i = 0 t a n i 2 i = Π i = 0 t ( a 2 i ) n i a^b = \Pi_{i=0}^{t}a^{n_i 2^i} = \Pi_{i=0}^{t}(a^{2^i})^{n_i} ab=Πi=0tani2i=Πi=0t(a2i)
Python系列(18)—— 取余运算符
Python中的取余运算符(Remainder Operator) 基本语法 取余运算符的语法很简单,就是两个数之间加上%符号。 remainder = dividend % divisor dividend(被除数)是被操作的数。divisor(除数)是用来除dividend的数。remainder(余数)是dividend除以divisor后的余数。 特性 正负数的取余:Pyth
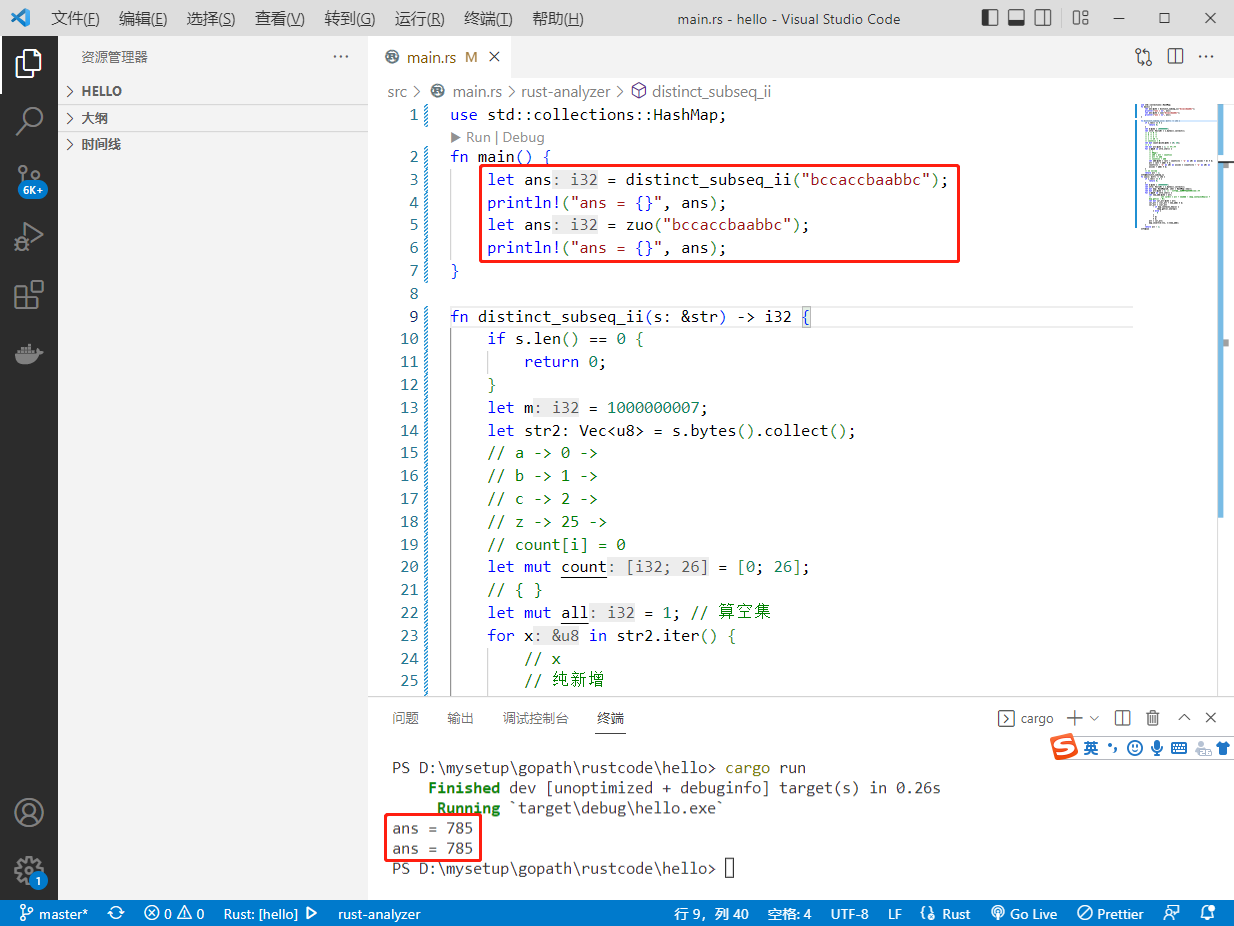
2022-10-01:给定一个字符串 s,计算 s 的 不同非空子序列 的个数 因为结果可能很大,所以返回答案需要对 10^9 + 7 取余 。 字符串的 子序列 是经由原字符串删除一些(也可能不删除
2022-10-01:给定一个字符串 s,计算 s 的 不同非空子序列 的个数 因为结果可能很大,所以返回答案需要对 10^9 + 7 取余 。 字符串的 子序列 是经由原字符串删除一些(也可能不删除)字符 但不改变剩余字符相对位置的一个新字符串。 输入: s = “abc”。 输出: 7。 答案2022-10-01: dp[0~25],保存26个字母结尾的子序列个数。 时间复杂度:O(N)。
Acwing---791. 高精度加法(减、乘、除、取余)——整数
高精度加法 1.题目2.基本思想3.代码实现4.总结 1.题目 给定两个正整数(不含前导 0),计算它们的和。 输入格式 共两行,每行包含一个整数。 输出格式 共一行,包含所求的和。 数据范围 1 ≤ 整数长度 ≤ 100000 1≤整数长度≤100000 1≤整数长度≤100000 输入样例: 12 23 输出样例: 35 2.基本思想 Jav
JS取余运算符 %,ES2023 新增数组方法Array.at
取余运算符(%)的作用就是用来两个操作数进行相除运算之后的余数。 注意,两个操作数取余是有循环范围的,这个范围为 0 - 第二个参数 - 1。 如下图: 对于6取余的话,得到的取余数据就会一直在0-5之间进行循环。 而如果第一个参数是一个负数的话,则范围为0 到 -第二个参数-1 有一中情况是,在数组中负数下标的话,应该获取到数据为length + 负数下标的数据,在es2023中,新增了一个
JavaScript之判断是否整数、取余、取整、进制、位或、ES6
MENU 方法一方式二方式三方式四方式五结束语 方法一 使用取余运算符判断,利用任何整数都会被1整除的原理,即余数是0的特点,通过这个规则来判断是否是整数。 let isInteger = (val) => val % 1 === 0;// trueisInteger(5);// falseisInteger(5.72); 以上输出可以看出这个函数挺好用,但对于字符
【例7.5】 取余运算(mod) 快速幂
1326:【例7.5】 取余运算(mod) 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 输入b,p,k的值,求bpmodk 的值。其中b,p,k×k为长整型数。 【输入】 输入b,p,k的值。 【输出】 求 bp mod k的值。 【输入样例】 2 10 9 【输出样例】 2^10 mod 9=7 思路: 可以直接暴力,for循环慢慢做,然后再Mod,但是
【Java入门练习100例】07.各数字的和——取余运算
🌲本文收录于专栏《Java入门练习100例》——试用于学完「Java基础语法」后的巩固提高及「LeetCode刷题」前的小试牛刀。 Java入门练习100例1-10源码 提取码: uqqe 题目描述 难度:简单 计算给定整数12345的各位上数字的和。 知识点 除法运算取余运算 解题思路 解题的关键在于如何拿到各个位上的数字。 举例:拿到34的个位和十位
【Java】取模(Math.floorMod())和取余(%)
文章目录 例子取余取模造成差别的原因参考资料 例子 public static void main(String[] args) {System.out.println("------Complementation------");System.out.println(7 % 4);System.out.println((-7) % 4);System.out.println(7
java算术运算符:取余(取模)%
本质:a % b = a - a /b * b; int num1 = 10 % 3; //10-(10/3)*3==>10-3*3==>1 int num2 = -10 % 3; //-10-((-10)/3)*3==>-10-(-3)*3==>-1 int num3 = 10 % -3; //10-[(10)/(-3)]*(-3)==>10-(-3)*(-3)==>1 int
10%-3 = -2 取余运算
在整数的除法中,只有能整除与不能整除两种情况。当不能整除时,就产生余数,所以余数问题在小学数学中非常重要。 取余数运算: a mod b = c 表示 整数a除以整数b所得余数为c。 余数的计算公式:c = a -⌊ a/b⌋ * b 其中,⌊ ⌋为向下取整运算符,向下取整运算称为Floor,用数学符号⌊ ⌋表示 例:⌊ 3.476 ⌋=3,⌊6.7546⌋=6,⌊-3.14159⌋= -4 如
【Python 千题 —— 基础篇】取余计算
题目描述 题目描述 编写一个程序,接受用户输入的两个数字,然后计算这两个数字取余后的结果,并输出结果。 输入描述 输入两个数字,用回车隔开两个数字。 输出描述 程序将计算这两个数字取余后的结果,并输出结果。 示例 示例 ① 73 输出: 1.0 代码讲解 下面是本题的代码: # 描述: 编写一个程序,接受用户输入的两个数字,然后计算这两个数字取余后的结果,并输
分治法 —— 取余运算 (快速幂)
取余运算 题目描述 给你三个整数 b,p,k,求 b^p mod k 输入格式 输入只有一行三个整数,分别代表 b,p,k 输出格式 输出一行一个字符串 b^p mod k=s,其中 b, p, k 分别为题目给定的值, s 为运算结果。 输入 2 10 9 输出 2^10 mod 9=7 说明/提示 2^10 = 10242 1024 mod 9=7 数据规模与约定 对于 100%10